“卓见杯”郑州轻工业大学第十五届程序设计大赛暨河南省高校邀请赛 题解12/12
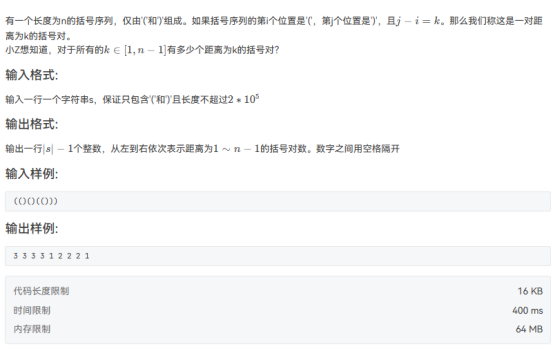
1计算括号对
例如(())
将其视作(a^1+a^2)*(a^-3+a^-4)
等于a^-3+2*a^-2+a^-1
这里a^-3的系数就是距离为3的左右括号的对数，a^-2的系数为距离为2的左右括号的对数
使用fft加速多项式乘法即可通过。
#include<bits/stdc++.h> using namespace std; #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define per(i,a,b) for(int i=(a);i>=(b);i--) typedef double db; typedef long long ll; struct cp { db x,y; cp(db real=0,db imag=0):x(real),y(imag){}; cp operator +(cp b)const{return {x+b.x,y+b.y};} cp operator -(cp b)const{return {x-b.x,y-b.y};} cp operator*(cp b)const{return {x*b.x-y*b.y,x*b.y+y*b.x};} }; using vcp=vector<cp>; using Poly=vector<int>; class Cipolla { int P,I2{}; using pll=pair<ll,ll>; }; #define MUL(a,b) (ll(a)*(b)%P) #define ADD(a,b) (((a)+=(b))>=P?(a)-=P:0) #define SUB(a,b) (((a)-=(b))<0?9a)+=P:0) const int P=1e9+7,N=2e5+10; Poly getINV(int L){ Poly inv(L);inv[1]=1; rep(i,2,L-1) inv[i]=MUL((P-P/i),inv[P%i]);return inv; } int POW(ll a,int b=P-2,ll x=1) { for(;b;b>>=1,a=a*a%P) if(b&1)x=x*a%P; return x; } //auto inv=getInv(N); namespace FFT{ const db pi=acos(-1); vcp Omega(int L){ vcp w(L);w[1]=1; for(int i=2;i<L;i<<=1){ auto w0=w.begin()+i/2,w1=w.begin()+i; cp wn(cos(pi/i),sin(pi/i)); for(int j=0;j<i;j+=2) w1[j]=w0[j>>1],w1[j+1]=w1[j]*wn; } return w ; } auto W=Omega(1<<19); void DIF(cp *a,int n){ cp x,y; for(int k=n>>1;k;k>>=1) for(int i=0;i<n;i+=k<<1) for(int j=0;j<k;j++) x=a[i+j],y=a[i+j+k],a[i+j+k]=(a[i+j]-y)*W[k+j],a[i+j]=x+y; } void IDIT(cp *a,int n){ cp x,y; for(int k=1;k<n;k<<=1) for(int i=0;i<n;i+=k<<1) for(int j=0;j<k;j++) x=a[i+j],y=a[i+j+k]*W[k+j],a[i+j+k]=x-y,a[i+j]=x+y; const db Inv=1. /n; rep(i,0,n-1)a[i].x*=Inv,a[i].y*=Inv; reverse(a+1,a+n); } } namespace Polynomial{ void DFT(vcp &a){FFT::DIF(a.data(),a.size());} void IDFT(vcp &a){FFT::IDIT(a.data(),a.size());} int norm(int n){return 1<<(__lg(n-1)+1);} void norm(Poly &a){if(!a.empty())a.resize(norm(a.size()),0); else a={0};} vcp &dot(vcp &a,vcp &b){rep(i,0,a.size()-1)a[i]=a[i]*b[i]; return a;} Poly operator *(ll k,Poly a){ Poly ans; for(auto i:a) ans.push_back(k*i); return ans; } Poly operator *(Poly a,Poly b){ int n=a.size()+b.size()-1; vcp c(norm(n)); rep(i,0,a.size()-1)c[i].x=a[i]; rep(i,0,b.size()-1)c[i].y=b[i]; DFT(c),dot(c,c),IDFT(c),a.resize(n); rep(i,0,n-1)a[i]=(int)(c[i].y*.5+.5); return a; } } using namespace Polynomial; char s[N]; int n; int main() { // freopen("1.in","r",stdin); ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); cin>>s+1; n=strlen(s+1)+10; int m=strlen(s+1); Poly vec1(n),vec2(n); for(int i=1;i<=m;i++) { if(s[i]=='(') vec1[m-i]=1; else vec2[i]=1; } Poly ans=vec1*vec2; // for(auto x:vec1) cout<<x<<" "; // cout<<endl; // for(auto x:vec2) cout<<x<<" "; // cout<<endl; // for(int i=0;i<vec1.size();i++) cout<<vec1[i]<<" "; // cout<<endl; // for(int i=0;i<vec2.size();i++) cout<<vec2[i]<<" "; // cout<<endl; // for(auto x: ans) cout<<x<<" "; // cout<<endl; bool flag=true; for(int i=1;i<m;i++) { if(flag) flag=false; else cout<<" "; cout<<ans[i+m]; } cout<<endl; // cout<<(1<<18)<<endl; return 0; }
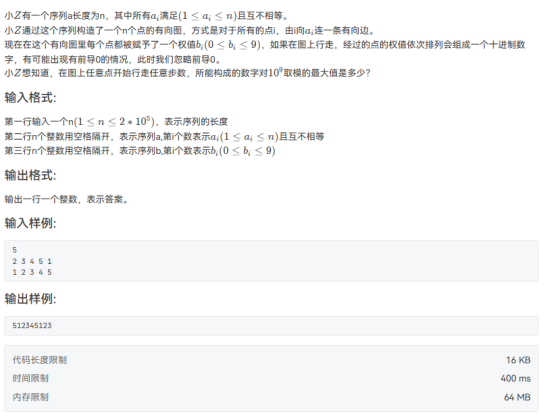
3最大的数
注意到模数是1e9，所以相当于问你走九步能走出来的最大的数字是多少。
所以我们大胆贪心，第一步当然去bi最大的点，然后循环八次：枚举当前位数能到达的点，枚举他们的出边看看下一步最大是多少。然后再次枚举他们的出边，看看为了达到最大值，下一步能到达的点有哪些。
刚开始写了一发只记录当前位数最大的数字，然后枚举所有该数字的点的出边。这样是不太对的。
#include<bits/stdc++.h> using namespace std; typedef long long ll; int read() { int x;scanf("%d",&x);return x; } int n,b[200010],ans[20]; vector<int>e[200010],pos[200010],can[20]; int main() { n=read(); for(int i=1;i<=n;i++) e[i].push_back(read()); for(int i=1;i<=n;i++) { b[i]=read(); pos[b[i]].push_back(i); } for(int i=9;i>=0;i--) { if(pos[i].size()) { ans[1]=i; can[1]=pos[i]; break; } } for(int i=1;i<=8;i++) { for(auto po:can[i]) { for(auto y:e[po]) ans[i+1]=max(ans[i+1],b[y]); } for(auto po:can[i]) { for(auto y:e[po]) if(b[y]==ans[i+1]) can[i+1].push_back(y); } cout<<ans[i]; } cout<<ans[9]; }
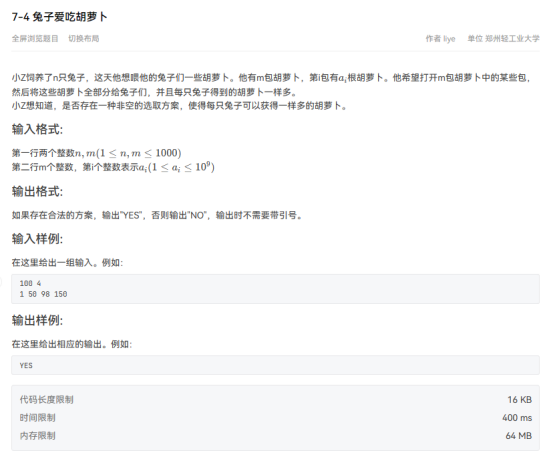
4兔子爱吃胡萝卜
考虑背包。我们并不关心ai，只关心ai%n的表现，所以直接让ai%=n。dp f[i][j]表示用前i包胡萝卜能到达%n=j的状态。那么f[i][j]=f[i-1][(j-a[i]+n)%n] | f[i-1][j]。最后看看f[n][0]是否为1即可
#include <bits/stdc++.h> #define endl '\n' using namespace std; typedef long long ll; const int N=1010; int f[N][N]; int a[N]; int n,m; int main() { ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); cin>>n>>m; for(int i=1;i<=m;i++) cin>>a[i],a[i]%=n; f[1][a[1]]=1; for(int i=2;i<=m;i++) { f[i][a[i]]=1; for(int j=0;j<n;j++) { f[i][(j+a[i])%n]|=f[i-1][j]; f[i][j]|=f[i-1][j]; } } // for(int i=1;i<=m;i++) // { // for(int j=0;j<n;j++) // { // cout<<f[i][j]<<" "; // } // cout<<endl; // } if(f[m][0]) cout<<"YES"<<endl; else cout<<"NO"<<endl; return 0; }
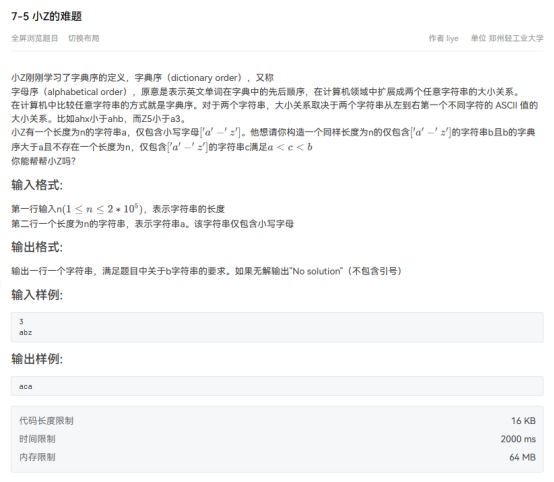
5小Z的难题
理解一下题意，发现要求类似a+1的字符串b。那么只有a串全为'z'才会导致no solution。否则我们给最后一个字符++，然后处理进位即可。
#include<bits/stdc++.h> using namespace std; typedef long long ll; int read() { int x;scanf("%d",&x);return x; } int n; char s[200010]; int check() { for(int i=0;i<n;i++) if(s[i]!='z') return 0; return 1; } int main() { n=read(); scanf("%s",s); if(check()) printf("No solution"); else { s[n-1]++; n--; while(s[n]=='z'+1) { s[n]='a'; n--; s[n]++; } printf("%s",s); } }
6莫比乌斯最大值isUsefulAlgorithm
刚开始写了一发sort后从大到小枚举ai*bj*gcd(ai,bj)，如果ai*bi*min(ai,bj)<ans的话就break，但是超时了，复杂度大概是n^2logn到n^3logn之间。
最后考虑枚举gcd(ax,by)为i，然后用(n/i)的复杂度去寻找最大的ax%i==0，by%i==0，那么对于gcd=i，答案即为ax*by*i(虽然有可能ax和by的gcd是i的若干倍）
复杂度为O(n/1+n/2+n/3+...+n/n)=O(nlogn)
#include<bits/stdc++.h> using namespace std; typedef long long ll; int read() { int x;scanf("%d",&x);return x; } int n,a[100010],b[100010]; ll ans; int main() { n=read(); for(int i=1;i<=n;i++) a[read()]=1; for(int j=1;j<=n;j++) b[read()]=1; for(int i=1;i<=100000;i++) { ll maxa=0,maxb=0; for(int j=i;j<=100000;j+=i) { if(a[j]) maxa=j; if(b[j]) maxb=j; } ans=max(ans,maxa*maxb*i); } cout<<ans; }
7爆米花
总爆米花数为(1+n)*n/2，合并次数为n-1，所以减去n-1即可。
#include<bits/stdc++.h> using namespace std; typedef long long ll; int read() { int x;scanf("%d",&x);return x; } ll n; int main() { n=read(); cout<<(1+n)*n/2-n+1; }
8what's 莫比乌斯最大值
考虑一个闲聊可能会解答多个问题，当且仅当这些问题都是闲聊的前缀。例如
abcdef可以解答what's a,what's ab ,what's abc
考虑贪心地选取最长的，还没被解答的，可以被解答的问题，一定是最优秀的。
对于每个闲聊都暴力地在前面枚举，用字符串哈希判断是否为前缀，复杂度O(n*n+n*strlen(s))。后来发现对于出现多次的同一个问题，需要去重，所以使用了map，复杂度O(n*nlogn)
#include<bits/stdc++.h> using namespace std; typedef long long ll; int read() { int x;scanf("%d",&x);return x; } int n,flag[1010],len[1010],ans; ll f[1010][1010]; string s[1010]; ll B=233,M=1e9+7; map<ll,int>o; void work(int i) { f[i][0]=s[i][0]; for(int j=1;j<len[i];j++) f[i][j]=(f[i][j-1]*B+s[i][j])%M; } int main() { // freopen("1.in","r",stdin); cin>>n; getline(cin,s[0]); for(int i=1;i<=n;i++) getline(cin,s[i]); for(int i=1;i<=n;i++) { if(s[i].substr(0,7)=="what's ") { s[i]=s[i].substr(7,s[i].length()-7); flag[i]=1; len[i]=s[i].length(); work(i); } else { len[i]=s[i].length(); work(i); int pos=0; for(int j=1;j<i;j++) { // cout<<"??"; if(flag[j]&&len[i]>=len[j]&&f[j][len[j]-1]==f[i][len[j]-1]&&len[j]>len[pos]&&o[f[j][len[j]-1]]==0) pos=j; } if(pos!=0) { ans++; flag[pos]=0; o[f[pos][len[pos]-1]]=1; } } } cout<<ans; }
10售卖车票
直接贪心，队友写的。
#include <bits/stdc++.h> #define endl '\n' using namespace std; typedef long long ll; const int N=6e5+10; struct node { int l,r; bool operator<(const node &a) { return l<a.l; } }p[N]; ll c[N]; int n,m,k; void add(int x,int y) { for(;x<=n;x+=x&-x) { c[x]+=y; } } ll ask(int x) { ll ans=0; for(;x;x-=x&-x) { ans+=c[x]; } return ans; } int main() { ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); cin>>n>>m>>k; for(int i=1;i<=m;i++) { cin>>p[i].l>>p[i].r; } sort(p+1,p+m+1); int t=1; priority_queue<pair<int,int>> q; for(int i=1;i<=n;i++) { while(t<=m&&p[t].l<=i) { int l=p[t].l; int r=p[t].r; add(l,1); add(r+1,-1); q.push({r,l}); t++; } int z=ask(i); if(z>k) { while(z>k) { auto it=q.top(); q.pop(); int l=it.second; int r=it.first; add(l,-1); add(r+1,1); z--; } } } // while(q.size()) // { // cout<<q.top().first<<" "<<q.top().second<<endl; // q.pop(); // } cout<<q.size()<<endl; return 0; }
11Alice and Bob
考虑有效的距离只有1000，所以先用字符串读入落点，用函数判断是否出靶，如果没出靶就算一下x*x+y*y。如果都没出靶就比一下x*x+y*y谁小即可。
#include<bits/stdc++.h> using namespace std; typedef long long ll; int read() { int x;scanf("%d",&x);return x; } char x[3][100010],y[3][100010]; int d[10]; int check(int t) { if(strlen(x[t])>6||strlen(y[t])>6) return 1;//chu ba ll xx=0,yy=0; for(int i=x[t][0]=='-'?1:0;i<strlen(x[t]);i++) xx=xx*10+x[t][i]-'0'; for(int i=y[t][0]=='-'?1:0;i<strlen(y[t]);i++) yy=yy*10+y[t][i]-'0'; d[t]=xx*xx+yy*yy; return d[t]>1000000; } int main() { scanf("%s%s",x[1],y[1]); scanf("%s%s",x[2],y[2]); if(check(1)&&check(2)) printf("Draw"); else if(check(1)) printf("Bob"); else if(check(2)) printf("Alice"); else { if(d[1]==d[2]) printf("Draw"); else if(d[1]<d[2]) printf("Alice"); else printf("Bob"); } }
12子序列
计数类问题
我首先写了一个离散化，用sum[i]表示数字i出现的次数
0对相等的方案数为$\prod (sum[i]+1)$，设为t 1对相等的方案数为 $\sum (C_{sum[i]}^{2} *\prod _{k!=i} (sum[i]+1)$ =$\sum( {C_{sum[i]}^{2}\over sum[i]+1} *\prod (sum[i]+1))$ =$\prod (sum[i]+1) *\sum {C_{sum[i]}^{2}\over sum[i]+1} $ 令$tsum=\sum {C_{sum[i]}^{2}\over sum[i]+1}$ 1对相等的方案数为 $t*tsum$ 2对相等的方案数为 ${\prod (sum[i]+1) \over 2 }* \sum( {C_{sum[i]}^{2} \over sum[i]+1} * \sum_{j!=i} ({ C_{sum[j]}^{2} \over sum[j]+1})) $ 如果把$C_{sum[j]}^{2} \over sum[j]+1$看做一个整体，那么后面这一块相当于有一堆这种数选两个相加 例如$1*2+1*3+2*1+2*3+3*1+3*2$=$(1+2+3)^2 -1^2-2^2-3^2$ 是和的平方减去平方的和 代码里令$tt=\sum{ {C_{sum[i]}^{2} \over sum[i]+1}}^2$为和的平方 则2对相等的方案数为$t/2*(tum*tsum-tt)$ 3对相等的方案数有两种 一种为一个数字出现3次，其他数字最多出现一次 方案数为$t*\sum{ C_{sum[i]}^{3} \over sum[i]+1} $，可以$O(n)$求得 另一种为三种数字出现2次，其他数字最多出现一次 方案数为${\prod (sum[i]+1) \over 6 }* \sum( {C_{sum[i]}^{2} \over sum[i]+1} * \sum_{j!=i} ({ C_{sum[j]}^{2} \over sum[j]+1}* \sum_{k!=i \&\&k!=j } ({ C_{sum[k]}^{2} \over sum[k]+1}))) $ 前面是老朋友$t/2$，后面这一坨是一堆数字取三个相乘加起来，我没有推式子，直接枚举第一项i 后面的可以代入2对相等的方案数求得的结果，为 ${t \over 6 } *{\sum({x}*((tsum-x )*(tsum-x )-tt+x*x))}$ 代码里每次先让$tsum-=x,tt-=x*x$,然后计算结果，再加回来 复杂度为$O(预处理nlogn+计算结果n)$
#include<bits/stdc++.h> using namespace std; typedef long long ll; int read() { int x;scanf("%d",&x);return x; } ll n,a[300010],b[300010],sum[300010],m,ni[300010]; ll inv[300010],fac[300010],mod=998244353; ll t=1,tsum,tt; ll quick(ll x,ll y) { ll t=1; while(y) { if(y&1) t=t*x%mod; x=x*x%mod; y=y/2; } return t; } ll C(ll b,ll a) { return fac[a]*inv[b]%mod*inv[a-b]%mod; } ll work() { ll ans=0; for(int i=1;i<=m;i++) { if(sum[i]>=2) { tt=(tt-C(2,sum[i])*ni[(sum[i]+1)]%mod*C(2,sum[i])%mod*ni[(sum[i]+1)]%mod)%mod; tsum=(tsum-C(2,sum[i])*ni[(sum[i]+1)]%mod)%mod; tt=(tt+mod)%mod; tsum=(tsum+mod)%mod; ans=(ans+C(2,sum[i])*ni[sum[i]+1]%mod*((tsum*tsum%mod-tt)%mod+mod)%mod)%mod; tt=(tt+C(2,sum[i])*ni[(sum[i]+1)]%mod*C(2,sum[i])%mod*ni[(sum[i]+1)]%mod)%mod; tsum=(tsum+C(2,sum[i])*ni[(sum[i]+1)]%mod)%mod; } } ans=ans*t%mod*ni[6]%mod; return (ans+mod)%mod; } int main() { ll ans=0; // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) b[i]=a[i]=read(); sort(b+1,b+1+n); m=unique(b+1,b+1+n)-b-1; for(int i=1;i<=n;i++) sum[lower_bound(b+1,b+1+m,a[i])-b]++; fac[0]=inv[0]=1; for(int i=1;i<=200010;i++) fac[i]=fac[i-1]*i%mod; inv[200010]=quick(fac[200010],mod-2); for(int i=200010;i>=1;i--) inv[i-1]=inv[i]*i%mod; for(int i=1;i<=200010;i++) ni[i]=quick(i,mod-2); for(int i=1;i<=m;i++) t=t*(sum[i]+1)%mod; for(int i=1;i<=m;i++) if(sum[i]>=2) tsum=(tsum+C(2,sum[i])*ni[(sum[i]+1)]%mod)%mod; for(int i=1;i<=m;i++) if(sum[i]>=2) tt=(tt+C(2,sum[i])*ni[(sum[i]+1)]%mod*C(2,sum[i])%mod*ni[(sum[i]+1)]%mod)%mod; ans=(ans+t*(tsum*tsum%mod-tt)%mod)%mod; ans=(ans+mod)%mod; ans=ans*ni[2]%mod; for(int i=1;i<=m;i++) if(sum[i]>=2) ans=(ans+C(2,sum[i])*ni[(sum[i]+1)]%mod*t%mod)%mod; ans=(ans+t-1)%mod; for(int i=1;i<=m;i++) if(sum[i]>=3) ans=(ans+C(3,sum[i])*t%mod*ni[sum[i]+1]%mod)%mod; ans=ans+work(); cout<<ans%mod<<endl; }
9 神奇的花
赛后重测A
#include <bits/stdc++.h> //#define endl '\n' using namespace std; typedef long long ll; const int N=1e5+10; ll d[N]; ll s,t; int n,k; ll calc(int y,int m,int d) { if(m<3) { y--; m+=12; } return 365ll*y+y/4ll-y/100ll+y/400ll+(153ll*(m-3ll)+2ll)/5ll+d-307ll; } int main() { int a,b,c; while(scanf("%d-%d-%d",&a,&b,&c)!=EOF) { s=calc(a,b,c); scanf("%d-%d-%d",&a,&b,&c); t=calc(a,b,c); scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d-%d-%d",&a,&b,&c); ll x=calc(a,b,c); if(x>=s&&x<=t) d[++k]=x-s+1; } d[++k]=0; d[++k]=t-s+2; sort(d+1,d+k+1); ll ans=0; ll cnt=0; for(int i=2;i<=k;i++) { ll x=d[i-1]; ll y=d[i]; ll u=x%7?x%7:7; ll v=y%7?y%7:7; ll _x=x+8-u; ll _y=y-v; if(y-x>=35) { cnt+=(_y-_x+1)/7*6; if(u<6) cnt+=7-u-1; if(v>1) cnt+=v-1; } else { for(ll z=x+1;z<=y-1;z++) { if(z%7) { cnt++; } } } ans=max(ans,cnt); // cout<<u<<" "<<v<<" "<<cnt<<endl; if(v==1||v==6||y-x==1) cnt=0; } if(s>t) cout<<0<<endl;else cout<<ans<<endl; } return 0; } //1234567 //1234567 //1234567
