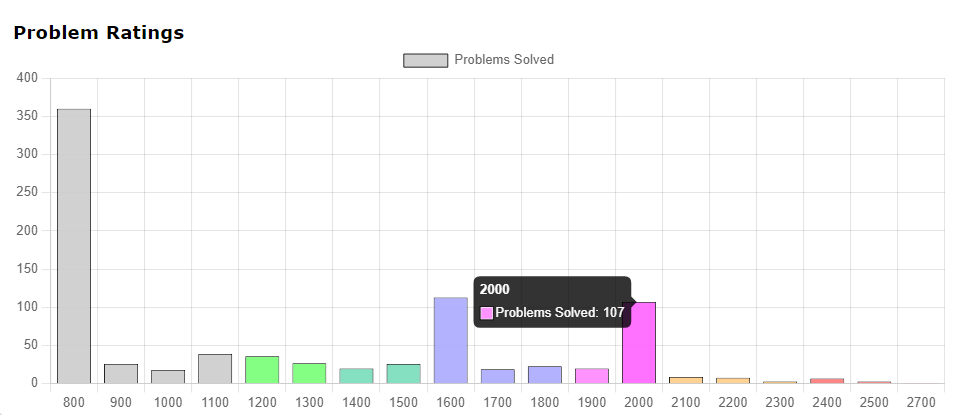
100道codeforces 2000分

考虑线段树维护区间里已配对的括号数,左边还没配对的右括号数,右边还没配对的左括号数。 区间询问,合并两个子区间即可。 int n; char s[1000010]; struct node { int c,l,r; }o[4000010]; node merge(node l,node r) { node tt; tt.c=l.c+r.c+min(l.l,r.r); tt.l=max(0,l.l-r.r)+r.l; tt.r=l.r+max(0,r.r-l.l); return tt; } void build(int x,int l,int r) { if(l==r) { o[x].c=0; if(s[l]=='(') o[x].l=1; else o[x].r=1; return ; } int mid=(l+r)/2; build(x*2,l,mid); build(x*2+1,mid+1,r); o[x]=merge(o[x*2],o[x*2+1]); } node ask(int x,int l,int r,int tl,int tr) { if(tl<=l&&r<=tr) return o[x]; int mid=(l+r)/2; if(tr<=mid) return ask(x*2,l,mid,tl,tr); if(tl>mid) return ask(x*2+1,mid+1,r,tl,tr); return merge(ask(x*2,l,mid,tl,tr),ask(x*2+1,mid+1,r,tl,tr)); } int main() { scanf("%s",s+1); n=strlen(s+1); build(1,1,n); for(int q=read();q;q--) { int l=read(),r=read(); printf("%d\n",ask(1,1,n,l,r).c*2); } }

考虑黑白格地设置,令奇数的上下左右都是偶数,偶数的上下左右都是奇数。 int n,m,x; void work() { n=read();m=read(); for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { x=read(); if((i+j)%2==x%2) printf("%d ",x); else printf("%d ",x+1); } printf("\n"); } } int main() { for(int t=read();t;t--) work(); }

首先不考虑aij有0的情况 那么分别求出f2[x][y],f5[x][y]表示到xy的路径上最少2的数量和最少5的数量,最佳答案即为min(f2[x][y],f5[x][y]) 比如如果是2的数量最少,那么我逆着倒回去求出最少2的数量的路径,该路径即为答案,且0的数量等于2的数量。因为如果5的数量更少的话,与“如果是2的数量最少”这个前提违背了。 那么如果存在0的话,我贪心的经过这个0,可以使得0的数量为1。那么当min(f2[x][y],f5[x][y])不为0时,走这个贪心路径很优秀。如果走其他路径可以没有0比如 1 1 1 1 0 1 1 1 1 那么我走别的更加优秀 为了不影响计算答案,在求f2[x][y],f5[x][y]时可以把0当作10来看待。 int n,x,y,tx,f2[1010][1010],f5[1010][1010],flag,posx,posy; stack<char>q; int main() { // freopen("1.in","r",stdin); memset(f2,0x3f,sizeof(f2)); memset(f5,0x3f,sizeof(f5)); f2[0][1]=f2[1][0]=f5[0][1]=f5[1][0]=0; n=read(); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) { tx=read(); f2[i][j]=f5[i][j]=0; if(tx==0) { flag=1; posx=i; posy=j; tx=10; } while(tx%5==0) { f5[i][j]++; tx=tx/5; } while(tx%2==0) { f2[i][j]++; tx=tx/2; } f2[i][j]+=min(f2[i-1][j],f2[i][j-1]); f5[i][j]+=min(f5[i-1][j],f5[i][j-1]); } if(flag&&f2[n][n]>=1&&f5[n][n]>=1)//走flag的话,答案可以为1,但是不走的话可能更小 { printf("1\n"); for(int i=1;i<posx;i++) printf("D"); for(int j=1;j<posy;j++) printf("R"); for(int i=posx;i<n;i++) printf("D"); for(int i=posy;i<n;i++) printf("R"); } else { if(f2[n][n]<f5[n][n]) printf("%d\n",f2[n][n]); else printf("%d\n",f5[n][n]); x=n,y=n; while(x!=1||y!=1) { if(x!=1&&y!=1) { if(f2[n][n]<f5[n][n]&&f2[x-1][y]<f2[x][y-1]||f5[n][n]<=f2[n][n]&&f5[x-1][y]<f5[x][y-1]) q.push('D'),x=x-1; else q.push('R'),y=y-1; } else if(x!=1) q.push('D'),x=x-1; else q.push('R'),y=y-1; } } while(q.size()) { printf("%c",q.top()); q.pop(); } }

考虑预处理出质数,然后大胆枚举质数的倍数,得到f[x][0]表示x的最小质因数,f[x][1]表示除了最小质因数之外的质因数的乘积。 为什么这样正确呢? 考虑f[x][1]不会被f[x][0]整除 f[x][0]也不会被f[x][1]里的质因数整除 所以是对的 int v[10000010],prime[700000],sum,f[10000010][2],x[500010],n; int main() { // freopen("1.in","r",stdin); for(int i=2;i<=10000000;i++) { if(v[i]==0) { v[i]=i; prime[++sum]=i; } for(int j=1;j<=sum;j++) { if(prime[j]>v[i]||prime[j]>10000000/i)break; v[i*prime[j]]=prime[j]; } } for(int i=1;i<=sum;i++) { for(int j=prime[i];j<=10000000;j+=prime[i]) { if(f[j][0]) f[j][1]*=prime[i]; else f[j][0]=prime[i],f[j][1]=1; } } n=read(); for(int i=1;i<=n;i++) { x[i]=read(); if(f[x[i]][1]<=1) printf("-1 "); else printf("%d ",f[x[i]][0]); } printf("\n"); for(int i=1;i<=n;i++) { if(f[x[i]][1]<=1) printf("-1 "); else printf("%d ",f[x[i]][1]); } }

二分答案,check函数是判断子序列的奇数位或者偶数位上的数字小于等于x的条件下,子序列的最长长度能否大于等于k。 int n,k,l,r,mid,a[200010]; int check(int x,int d) { int len=0; for(int i=1;i<=n;i++) { if(len%2==d)//需要小于等于x { while(i<=n&&a[i]>x) i++; if(i<=n) len++; } else//否则随意点 len++; } return len>=k; } int main() { // freopen("1.in","r",stdin); n=read();k=read(); for(int i=1;i<=n;i++) a[i]=read(); l=1,r=1e9; while(l+1<r) { mid=(l+r)/2; if(check(mid,0)||check(mid,1)) r=mid; else l=mid; } if(check(l,0)||check(l,1)) printf("%d",l); else printf("%d",r); }

ai的范围比较小,所以可以从这里下手。 考虑对于每个i为右端点的情况,计算所有左端点的得分,取max。而ai的范围比较小,所以考虑把ai的值相同的放在一起考虑。 综上用vector做单调队列,线段树维护区间前缀和的最小值即可。复杂度n*60*logn struct node { int i,v; }; vector<node>o; int minn[400010],n,a,sum,ans; void build(int x,int l,int r) { if(l==r) { if(l!=0) minn[x]=3e7; return ; } int mid=(l+r)/2; build(x*2,l,mid); build(x*2+1,mid+1,r); minn[x]=min(minn[x*2],minn[x*2+1]); } void change(int x,int l,int r,int i,int v) { if(l==r) { minn[x]=v; return ; } int mid=(l+r)/2; if(i<=mid) change(x*2,l,mid,i,v); else change(x*2+1,mid+1,r,i,v); minn[x]=min(minn[x*2],minn[x*2+1]); } int ask(int x,int l,int r,int tl,int tr) { if(tl<=l&&r<=tr) return minn[x]; int t=3e7,mid=(l+r)/2; if(tl<=mid) t=ask(x*2,l,mid,tl,tr); if(tr>mid) t=min(t,ask(x*2+1,mid+1,r,tl,tr)); return t; } int main() { // freopen("1.in","r",stdin); n=read(); build(1,0,n); o.push_back({0,100}); for(int i=1;i<=n;i++) { a=read(); sum=sum+a; change(1,0,n,i,sum); while(o.size()&&o.back().v<=a) o.pop_back(); o.push_back({i,a}); for(int j=1;j<o.size();j++) ans=max(ans,sum-ask(1,0,n,o[j-1].i,o[j].i-1)-o[j].v); } printf("%d",ans); }

顺着想就好了。 考虑枚举新的b,那么新的a要从b的因子中选,新的c要从b的倍数中选,要么是c-c%tb,要么是c+tb-c%tb。复杂度t*10000*(sqrt(10000)) 本来tb只枚举到了10000,但是被数据上了一课:1 137 10000 10000 可以变成 2 137 10001 10001 int a,b,c,ans,ansa,ansb,ansc,sum; void work() { a=read();b=read();c=read(); ans=a-1+b-1+c-1; ansa=1;ansb=1;ansc=1; for(int tb=1;tb<=30000;tb++) { if(abs(b-tb)>=ans)continue; for(int ta=1;ta<=sqrt(tb);ta++) { if(tb%ta==0) { sum=abs(b-tb)+min(abs(a-ta),abs(a-tb/ta))+min(c%tb,tb-c%tb); if(sum<ans) { if(abs(a-ta)<=abs(a-tb/ta)) ansa=ta; else ansa=tb/ta; if(c%tb<tb-c%tb) ansc=c-c%tb; else ansc=c+tb-c%tb; ansb=tb; ans=sum; } } } } printf("%d\n%d %d %d\n",ans,ansa,ansb,ansc); } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

问题等价于是否存在长为2或者长为3的区间,k为中位数 int n,a[100010],k,flag; void work() { n=read();k=read();flag=0; for(int i=1;i<=n;i++) { a[i]=read(); if(a[i]==k) flag=1; } if(flag==0) { printf("no\n"); return ; } if(n==1) { printf("yes\n"); return ; } for(int i=1;i<n;i++) { if(a[i]<k)continue; if(a[i+1]>=k||i+2<=n&&a[i+2]>=k) { printf("yes\n"); return ; } } printf("no\n"); return ; } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

卡ll 首先判断一下是否有解,有解的话用exgcd求得xw+dy=p的一个特解,然后可以贪心地令y取到大于等于0的最小值,此时x+y最小,然后判断z是否大于等于0,x是否大于等于0即可,有解的话可以再换回ll来输出 __int128 exgcd(__int128 a,__int128 b,__int128 &x,__int128 &y) { if(b==0) { x=1,y=0; return a; } __int128 d=exgcd(b,a%b,x,y); __int128 z=x; x=y; y=z-y*(a/b); return d; } __int128 n,p,w,d,x,y,gcdd; int main() { // freopen("1.in","r",stdin); n=read();p=read();w=read();d=read(); gcdd=exgcd(w,d,x,y); if(p%gcdd!=0) { printf("-1\n"); return 0; } x=x*(p/gcdd); y=y*(p/gcdd); if(y<0) { ll t=(-y+w/gcdd-1)/(w/gcdd); y=y+t*(w/gcdd); x=x-t*(d/gcdd); } if(y>=w/gcdd) { ll t=y/(w/gcdd); y=y-t*(w/gcdd); x=x+t*(d/gcdd); } if(x+y>n||x<0) printf("-1"); else { ll tx=x,ty=y,tz=n-tx-ty; printf("%lld %lld %lld",tx,ty,tz); } }

kmp的经典应用 char s[100010]; int n,pi[100010]; ll ans[100010]; stack<pair<int,ll>>q; int main() { // freopen("1.in","r",stdin); scanf("%s",s); n=strlen(s); for(int i=1;i<n;i++) { int j=pi[i-1]; while(j&&s[i]!=s[j]) j=pi[j-1]; if(s[i]==s[j]) j++; pi[i]=j; } for(int i=0;i<n;i++) ans[i]=1; for(int i=n-1;i>=1;i--) ans[pi[i]-1]+=ans[i]; while(n) { q.push({n,ans[n-1]}); n=pi[n-1]; } printf("%d\n",q.size()); while(q.size()) { printf("%d %lld\n",q.top().first,q.top().second); q.pop(); } }

dfs染色,把初始点和初始点能到达的完整的冰赋值为1 那么如果结束的点是破碎的,就需要周围有一个点是初始点或者是初始点能到的完整的。 如果结果的点是完整的,需要周围有一个点是初始点,有一个点是初始点能到达的完整的;或者周围有两个初始点能到达的完整的。表现在v数组上就是有两个v[x+dx[i]][y+dy[i]]=1 char s[510][510]; int v[510][510],dx[]={0,0,1,-1},dy[]={1,-1,0,0}; int n,m,c1,c2,r1,r2; void work(int x,int y) { if(v[x][y]) return ; v[x][y]=1; for(int i=0;i<4;i++) if(s[x+dx[i]][y+dy[i]]=='.') work(x+dx[i],y+dy[i]); } int main() { // freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++) scanf("%s",s[i]+1); r1=read();c1=read(); r2=read();c2=read(); work(r1,c1); if(s[r2][c2]=='.')// { int sum=0; for(int i=0;i<4;i++) sum+=v[r2+dx[i]][c2+dy[i]]; if(sum>=2) printf("YES"); else printf("NO"); } else { for(int i=0;i<4;i++) if(v[r2+dx[i]][c2+dy[i]]) { printf("YES"); return 0; } printf("NO"); } }

简单地开20个线段树,区间异或等价于每一位的区间翻转。 ll c[400010][21]; int a[100010],lazy[400010][21]; int n,m; void build(int x,int l,int r) { if(l==r) { for(int i=0;i<=20;i++) if(a[l]&(1<<i)) c[x][i]=1<<i; return ; } int mid=(l+r)/2; build(x*2,l,mid); build(x*2+1,mid+1,r); for(int i=0;i<=20;i++) c[x][i]=c[x*2][i]+c[x*2+1][i]; } void pushdown(int x,int l,int r,int i) { int mid=(l+r)/2; lazy[x][i]=0; c[x*2][i]=(1ll<<i)*(mid-l+1)-c[x*2][i]; c[x*2+1][i]=(1ll<<i)*(r-mid)-c[x*2+1][i]; lazy[x*2][i]^=1; lazy[x*2+1][i]^=1; } void add(int x,int l,int r,int tl,int tr,int i) { if(tl<=l&&r<=tr) { lazy[x][i]^=1; c[x][i]=(1ll<<i)*(r-l+1)-c[x][i]; return ; } if(lazy[x][i]) pushdown(x,l,r,i); int mid=(l+r)/2; if(tl<=mid) add(x*2,l,mid,tl,tr,i); if(tr>mid) add(x*2+1,mid+1,r,tl,tr,i); c[x][i]=c[x*2][i]+c[x*2+1][i]; } ll ask(int x,int l,int r,int tl,int tr) { ll t=0; if(tl<=l&&r<=tr) { for(int i=0;i<=20;i++) t=t+c[x][i]; return t; } for(int i=0;i<=20;i++) if(lazy[x][i]) pushdown(x,l,r,i); int mid=(l+r)/2; if(tl<=mid) t=t+ask(x*2,l,mid,tl,tr); if(tr>mid) t=t+ask(x*2+1,mid+1,r,tl,tr); return t; } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) a[i]=read(); build(1,1,n); for(int i=read();i;i--) { if(read()&1) { int tl=read(),tr=read(); printf("%lld\n",ask(1,1,n,tl,tr)); } else { int tl=read(),tr=read(),tx=read(); for(int i=0;i<=20;i++) if(tx&(1<<i)) add(1,1,n,tl,tr,i); } } }

spfa牛逼 首先不管可删边,跑一个最短路。然后对于可删边,按边权从小到大枚举,如果小于最短路则不删,并用spfa更新其他点的最短路。 一共45个测试点,用Dijkstra会在第42个点T掉,用spfa则不会。 struct node { ll d;int i; friend bool operator<(node a,node b) { return a.d>b.d; } }t; queue<int>q; priority_queue<node>o; int n,m,k,ans,tx,ty,tv; int vis[100010]; vector<int>e[100010],v[100010]; ll d[100010]; int main() { // freopen("1.in","r",stdin); n=read();m=read();k=read(); for(int i=1;i<=m;i++) { tx=read(),ty=read(),tv=read(); e[tx].push_back(ty); v[tx].push_back(tv); e[ty].push_back(tx); v[ty].push_back(tv); } memset(d,0x3f,sizeof(d)); d[1]=0; q.push(1); while(q.size()) { tx=q.front(); q.pop(); vis[tx]=0; for(int i=0;i<e[tx].size();i++) { if(d[tx]+v[tx][i]<d[e[tx][i]]) { d[e[tx][i]]=d[tx]+v[tx][i]; if(vis[e[tx][i]]==0) { vis[e[tx][i]]=1; q.push(e[tx][i]); } } } } for(int i=1;i<=k;i++) { ty=read(),tv=read(); o.push({tv,ty}); } ans=k; while(o.size()) { t=o.top();o.pop(); if(t.d>=d[t.i]) continue; ans--; d[t.i]=t.d; q.push(t.i); while(q.size()) { tx=q.front(); q.pop(); vis[tx]=0; for(int i=0;i<e[tx].size();i++) { if(d[tx]+v[tx][i]<d[e[tx][i]]) { d[e[tx][i]]=d[tx]+v[tx][i]; if(vis[e[tx][i]]==0) { vis[e[tx][i]]=1; q.push(e[tx][i]); } } } } } printf("%d",ans); }

一个dfs搞定。 考虑更新ax为从根到x的最小的花费a,每次把子树没处理完的0->1和1->0拿过来在我这里处理一下,处理不掉的让父亲处理即可。 ll ans; int n,a[200010],b[200010],c[200010],sum[200010][2]; vector<int>e[200010]; void dfs(int x,int fa) { if(b[x]!=c[x]) sum[x][b[x]]++; for(auto y:e[x]) { if(fa==y)continue; a[y]=min(a[y],a[x]); dfs(y,x); sum[x][0]+=sum[y][0]; sum[x][1]+=sum[y][1]; } int t=min(sum[x][0],sum[x][1]); ans=ans+2ll*t*a[x]; sum[x][0]-=t; sum[x][1]-=t; } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) { a[i]=read(); b[i]=read(); c[i]=read(); } for(int i=1;i<n;i++) { int tx=read(),ty=read(); e[tx].push_back(ty); e[ty].push_back(tx); } dfs(1,0); if(sum[1][0]||sum[1][1]) printf("-1"); else printf("%lld",ans); }

想象一下,先把有向边捋顺,然后现在往里往里加边 我们当然希望顺着原来的顺序加。 那么如果他俩原来没啥顺序的话,我人为地令从小节点往大节点加,这样就可以实现有向无环。 如果存在点d为0则证明只看有向边已经有环了,那么再加边也是有环的,所以输出NO int n,m,sum,ru[200010],x,d[200010]; vector<int>e[200010]; struct node{int x,y;}o[200010]; queue<int>q; void work() { n=read();m=read(); for(int i=1;i<=n;i++) { ru[i]=0; e[i].clear(); } sum=0; for(int i=1;i<=m;i++) { if(read()&1) { x=read(); int y=read(); e[x].push_back(y); ru[y]++; } else { sum++; o[sum].x=read(); o[sum].y=read(); } } for(int i=1;i<=n;i++) if(ru[i]==0) { d[i]=1; q.push(i); } else d[i]=0; while(q.size()) { x=q.front(); q.pop(); for(auto y:e[x]) { ru[y]--; if(ru[y]==0) { d[y]=d[x]+1; q.push(y); } } } for(int i=1;i<=n;i++) if(d[i]==0) { printf("NO\n"); return ; } printf("YES\n"); for(int i=1;i<=sum;i++) { if(o[i].x>o[i].y) swap(o[i].x,o[i].y); if(d[o[i].x]<d[o[i].y]) printf("%d %d\n",o[i].x,o[i].y); else if(d[o[i].x]>d[o[i].y]) printf("%d %d\n",o[i].y,o[i].x); else printf("%d %d\n",o[i].x,o[i].y); } for(x=1;x<=n;x++) for(auto y:e[x]) printf("%d %d\n",x,y); } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

考虑一条链的话,可以贪心地从后往前看:如果当前尾巴的值大于0,就先操作,把值加到下一个点,否则就最后操作,不让他的负数影响到前面的值,类似与求最大子段和。 对于有向无环图,考虑拓扑排序,如果值大于0就加到一个队列里,否则加到一个栈里 然后输出 int n,b[200010],ru[200010]; ll ans,a[200010]; queue<int>q,print1; stack<int>print0; int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) a[i]=read(); for(int i=1;i<=n;i++) { b[i]=read(); if(b[i]==-1) b[i]++; ru[b[i]]++; } for(int i=1;i<=n;i++) if(ru[i]==0) q.push(i); while(q.front()!=0) { int x=q.front(); q.pop(); ans=ans+a[x]; if(a[x]>0) { print1.push(x);//大于0的 ru[b[x]]--; a[b[x]]+=a[x]; } else { print0.push(x);//小于等于0的 ru[b[x]]--; } if(ru[b[x]]==0) q.push(b[x]); } printf("%lld\n",ans); while(print1.size()) { printf("%d ",print1.front()); print1.pop(); } while(print0.size()) { printf("%d ",print0.top()); print0.pop(); } }

考虑二分答案,对于所需的x,可以把aij看做是01:大于等于x的是1,小于x的是0,那么需要两行或起来每一位都是1。 所以用fi记录01串为i的数组的任意一个下标,则当存在i|j每一位都是1时,存在答案,答案为fi和fj。 int f[400],a[300010][10],now,tot; int n,m,ans1,ans2; int check(int x) { for(int i=0;i<=tot;i++) f[i]=0;//记录下标 for(int i=1;i<=n;i++) { now=0; for(int j=1;j<=m;j++) if(a[i][j]>=x) now=now*2+1; else now=now*2; f[now]=i; } for(int i=0;i<=tot;i++) { for(int j=0;j<=tot;j++) { if(f[i]&&f[j]&&(i|j)==tot) { ans1=f[i]; ans2=f[j]; return 1; } } } return 0; } int main() { // freopen("1.in","r",stdin); n=read();m=read(); tot=1<<m; tot--; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) a[i][j]=read(); int l=0,r=1e9,mid; while(l+1<r) { mid=(l+r)/2; if(check(mid)) l=mid; else r=mid; } if(check(r)) printf("%d %d\n",ans1,ans2); else if(check(l)) printf("%d %d\n",ans1,ans2); }

一点也不会,抄题解了 void work() { int n=read(); printf("%.9lf\n",cos(acos(-1)/4/n)/sin(acos(-1)/2/n)); } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

考虑在#的连通块的边界放南极,#的每个连通块内部放一个北极,所以问题转化成求连通块数量。 接下来考虑无解的情况。首先注意到不能存在#.....#这种情况,其次就是如果某一列都有#,那么不能存在某一行没有#。如果某一行都有#,则不能存在某一列没有#。 int n,m; char s[1010][1010]; int ans,fa[2000000],sum1[1010],sum2[1010],f1[1010],f2[1010],tot1,tot2; int get(int x) { return fa[x]==x?x:fa[x]=get(fa[x]); } void merge(int x,int y) { if(get(x)==get(y)) return ; fa[get(x)]=fa[get(y)]; } int main() { // freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++) scanf("%s",s[i]+1); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) { sum1[i]+=(s[i][j]=='#'); sum2[j]+=(s[i][j]=='#'); f1[i]|=(s[i][j]=='#'); f2[j]|=(s[i][j]=='#'); } for(int i=1;i<=n;i++) tot1=tot1+f1[i]; if(tot1==n)//如果每一行都有#,则不允许某一列没有# { for(int j=1;j<=m;j++) if(sum2[j]==0) { printf("-1"); return 0; } } for(int j=1;j<=m;j++) tot2+=tot2+f2[j]; if(tot2==m)//如果每一列都有#,则不允许某一行没有# { for(int i=1;i<=n;i++) if(sum1[i]==0) { printf("-1"); return 0; } } for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(s[i][j]=='#'&&s[i][j+1]=='.') { for(;j<=m;j++) if(s[i][j]=='.'&&s[i][j+1]=='#') { printf("-1"); return 0; } break; } for(int j=1;j<=m;j++) for(int i=1;i<=n;i++) if(s[i][j]=='#'&&s[i+1][j]=='.') { for(;i<=n;i++) if(s[i][j]=='.'&&s[i+1][j]=='#') { printf("-1"); return 0; } break; } for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) fa[i*m+j]=i*m+j; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) { if(s[i][j]=='#'&&s[i-1][j]=='#') merge(i*m+j,i*m+j-m); if(s[i][j]=='#'&&s[i][j-1]=='#') merge(i*m+j,i*m+j-1); } for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(get(fa[i*m+j])==i*m+j&&s[i][j]=='#') ans++; printf("%d",ans); }

区间dp,fij为删掉区间ij所需次数 那么sl要么花费1次删掉,要么枚举一个i使得si=sl,先删掉区间[l+1,i-1],再把sl和[i,r]一块删掉,花费是f[l+1][i-1]+f[i][r] char s[510]; int n,f[510][510],ans; int main() { // freopen("1.in","r",stdin); n=read(); scanf("%s",s+1); for(int i=1;i<=n;i++) f[i][i]=1; for(int len=2;len<=n;len++) for(int l=1,r=len;r<=n;l++,r++) { if(s[l]==s[l+1]) f[l][r]=f[l+1][r]; else f[l][r]=f[l+1][r]+1; for(int i=l+2;i<=r;i++) if(s[l]==s[i]) f[l][r]=min(f[l][r],f[l+1][i-1]+f[i][r]); } printf("%d",f[1][n]); }

首先是看错题了,题目需要的是恰好有一个位置不同 其次是ull自然溢出会被卡,所以需要自己弄一个mod 总之哈希做法是把n个串的哈希值扔到set里,然后对于m个串,每个串枚举哪里不同,变成了什么,重新计算哈希值,判断是否在set里 set<pair<ll,ll>>o; int len,n,m; char s[600010]; ll f[600010],p[600010],f1[600010],p1[600010]; ll mod=1e9+7; void work() { for(int j=1;j<=len;j++) { for(int x='a';x<='z';x++) { if(s[j]==x)continue; ll t=((f[len]-(s[j]-x)*p[len-j])%mod+mod)%mod; ll t1=((f1[len]-(s[j]-x)*p1[len-j])%mod+mod)%mod; if(o.count({t,t1})) { printf("YES\n"); return ; } } } printf("NO\n"); } int main() { // freopen("1.in","r",stdin); n=read();m=read(); p[0]=p1[0]=1; for(int i=1;i<=600000;i++) { p[i]=p[i-1]*233%mod; p1[i]=p1[i-1]*131%mod; } for(int i=1;i<=n;i++) { scanf("%s",s+1); ull now=0,now1=0; len=strlen(s+1); for(int j=1;j<=len;j++) { now=(now*233+s[j])%mod; now1=(now1*131+s[j])%mod; } o.insert({now,now1}); } for(int i=1;i<=m;i++) { scanf("%s",s+1); len=strlen(s+1); for(int j=1;j<=len;j++) { f[j]=(f[j-1]*233+s[j])%mod; f1[j]=(f1[j-1]*131+s[j])%mod; } work(); } }

用kmp算法得到新串到哪是匹配的,然后往里加即可 char s[4000010],t[4000010]; int len,f[4000010];; int main() { // freopen("1.in","r",stdin); // freopen("2.out","w",stdout); len=0; int n=read(); cin>>s; len=strlen(s); for(n--;n;n--) { cin>>t; int tlen=strlen(t); t[tlen]='#'; tlen++; int maxx=min(tlen-1,len); for(int i=max(0,len-tlen);i<len;i++) { t[tlen]=s[i]; tlen++; } for(int i=1;i<tlen;i++) { int j=f[i-1]; while(j&&t[i]!=t[j]) j=f[j-1]; if(t[i]==t[j]) j++; f[i]=j; } for(int i=f[tlen-1];t[i]!='#';i++) { s[len]=t[i]; len++; } // cout<<t<<' '<<s<<endl; } cout<<s;

考虑先用2*(n-1)步,把ai都转移到a1上,然后再用n-1步放回到ai上。 转移的过程是先用a1把ai补足到i的倍数,这一步一定可以,因为在转移ai时,a1拿到了1到i-1的所有值,a1>=i-1,所以可以把ai补足到i的倍数。 int n,sum,a[10010]; void work() { n=read();sum=0; for(int i=1;i<=n;i++) { a[i]=read(); sum=sum+a[i]; } if(sum%n!=0) { printf("-1\n"); return ; } sum=sum/n; printf("%d\n",(n-1)*3); for(int i=2;i<=n;i++) { if(a[i]%i==0) printf("%d %d %d\n",1,i,0); else printf("%d %d %d\n",1,i,i-a[i]%i),a[i]+=i-a[i]%i; printf("%d %d %d\n",i,1,a[i]/i); a[1]+=a[i]; } for(int i=2;i<=n;i++) printf("%d %d %d\n",1,i,sum); } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

怎么感觉越来越简单了。。 考虑缩点成有向无环图之后,答案即为没有入边的点的数量。如果起点所在的强连通分量也没有入边,那么可以让答案--。 int dfn[5010],low[5010],num,ins[5010],c[5010]; vector<int>e[5010]; stack<int>q; int n,m,s,cnt,ans,ru[5010]; void targan(int x) { dfn[x]=low[x]=++num; q.push(x);ins[x]=1; for(auto y:e[x]) { if(!dfn[y]) { targan(y); low[x]=min(low[x],low[y]); } else if(ins[y]) low[x]=min(low[x],low[y]); } if(dfn[x]==low[x]) { cnt++; int y; do { y=q.top();q.pop(); ins[y]=0; c[y]=cnt; }while(x!=y); } } int main() { // freopen("1.in","r",stdin); n=read();m=read();s=read(); for(int i=1;i<=m;i++) { int tx=read(); e[tx].push_back(read()); } for(int i=1;i<=n;i++) if(!dfn[i]) targan(i); for(int x=1;x<=n;x++) for(auto y:e[x]) if(c[x]!=c[y]) ru[c[y]]++; for(int i=1;i<=cnt;i++) if(ru[i]==0) ans++; if(ru[c[s]]==0) ans--; cout<<ans; }

用优先队列维护所有边,边权除以二向下取整后能减少多少。 每次贪心地令能减少最大的边除以二。 struct edge{int y,w;}; ll w[100010],sum[100010],now,S; int n,ans; priority_queue<pair<ll,int>>q; vector<edge>e[100010]; void dfs(int x,int fa) { if(e[x].size()==1&&e[x][0].y==fa)//是叶子 sum[x]=1; else for(auto t:e[x]) { if(t.y==fa)continue; dfs(t.y,x); sum[x]+=sum[t.y]; q.push({t.w*sum[t.y]-t.w/2*sum[t.y],t.y}); w[t.y]=t.w; now=now+t.w*sum[t.y]; } } void work() { n=read();S=read(); for(int i=1;i<=n;i++) { sum[i]=0; e[i].clear(); } while(q.size()) q.pop(); for(int i=1;i<n;i++) { int tx=read(),ty=read(),tw=read(); e[tx].push_back({ty,tw}); e[ty].push_back({tx,tw}); } ans=0;now=0; dfs(1,0); while(now>S) { int tx=q.top().second; q.pop(); now=now-w[tx]*sum[tx]+w[tx]/2*sum[tx]; w[tx]/=2; q.push({w[tx]*sum[tx]-w[tx]/2*sum[tx],tx}); ans++; } printf("%d\n",ans); } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

不懂,抄的https://blog.csdn.net/weixin_43911574/article/details/108431672 int n,x; stack<int>q; ll ans; int main() { n=read(); for(int i=1;i<=n;i++) { x=read(); ans=ans+x/2; if(x%2==0) continue; if(q.size()&&(q.top()&1)!=(i&1)) ans++,q.pop(); else q.push(i); } cout<<ans; }

这个要求其实是除了a1的ai都是a1的倍数。 所以考虑枚举a1,其他数字的选择方案是C(k-1,n/a1-1),预处理组合数做一下即可。 ll mod=998244353ll; ll quick(ll a,ll b) { ll t=1; while(b) { if(b&1) t=t*a%mod; a=a*a%mod; b=b/2; } return t; } ll f[500010],inv[500010]; ll C(ll m,ll n) { return f[n]*inv[m]%mod*inv[n-m]%mod; } ll n,k,ans; int main() { n=read();k=read(); f[0]=1; for(int i=1;i<=500000;i++) f[i]=f[i-1]*i%mod; inv[500000]=quick(f[500000],mod-2); for(int i=499999;i>=0;i--) inv[i]=inv[i+1]*(i+1)%mod; for(int i=1;n/i-1>=k-1;i++) ans=(ans+C(k-1,n/i-1))%mod; cout<<ans; }

考虑分层地做dfs序,按dfs序放在两个vector里,l1,r1记录当x被修改时,这个区间里的数字要被减小。l2,r2记录当x被修改时,这个区间里的数字要被增加。然后线段树维护一下区间加法,单点询问(这个部分也可以用差分树状数组)。 int n,m,a[200010],d[200010],fa[200010],l1[200010],r1[200010],l2[200010],r2[200010]; int sum[2][800010],lazy[2][800010]; int sum1[200010],sum2[200010]; vector<int>e[200010],v[200010]; queue<int>q; void build(int x,int l,int r,int d) { if(l==r) { sum[d][x]=a[v[d][l]]; return ; } int mid=(l+r)/2; build(x*2,l,mid,d); build(x*2+1,mid+1,r,d); } void pushdown(int x,int l,int r,int d) { if(lazy[d][x]==0) return ; int mid=(l+r)/2; lazy[d][x*2]+=lazy[d][x]; lazy[d][x*2+1]+=lazy[d][x]; sum[d][x*2]+=lazy[d][x]*(mid-l+1); sum[d][x*2+1]+=lazy[d][x]*(r-mid); lazy[d][x]=0; } void add(int x,int l,int r,int tl,int tr,int val,int d) { if(tl<=l&&r<=tr) { lazy[d][x]+=val; sum[d][x]+=(l-r+1)*val; return ; } pushdown(x,l,r,d); int mid=(l+r)/2; if(tl<=mid) add(x*2,l,mid,tl,tr,val,d); if(tr>mid) add(x*2+1,mid+1,r,tl,tr,val,d); } int ask(int x,int l,int r,int pos,int d) { if(l==r) return sum[d][x]; pushdown(x,l,r,d); int mid=(l+r)/2; if(pos<=mid) return ask(x*2,l,mid,pos,d); return ask(x*2+1,mid+1,r,pos,d); } void dfs(int x) { sum1[x]=1; sum2[x]=0; l1[x]=v[1-(d[x]&1)].size(); for(auto y:e[x]) { if(y==fa[x])continue; fa[y]=x; d[y]=d[x]+1; v[1-(d[x]&1)].push_back(y); dfs(y); sum1[x]+=sum2[y]; sum2[x]+=sum1[y]; } } int main() { // freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++) a[i]=read(); for(int i=1;i<n;i++) { int tx=read();int ty=read(); e[tx].push_back(ty); e[ty].push_back(tx); } q.push(1); e[1].push_back(0); v[0].push_back(0); v[1].push_back(0); v[0].push_back(1); dfs(1); for(int i=1;i<v[0].size();i++) { int x=v[0][i]; r1[x]=l1[x]+sum2[x]-1; l2[x]=i; r2[x]=i+sum1[x]-1; } r1[0]=1; for(int i=1;i<v[1].size();i++) { int x=v[1][i]; r1[x]=l1[x]+sum2[x]-1; l2[x]=i; r2[x]=i+sum1[x]-1; } build(1,1,v[0].size()-1,0); if(v[1].size()>1) build(1,1,v[1].size()-1,1); for(;m;m--) { if(read()&1) { int x=read();int val=read(); if(v[d[x]&1].size()>1) add(1,1,v[d[x]&1].size()-1,l2[x],r2[x],val,d[x]&1); if(sum2[x]&&v[1-(d[x]&1)].size()>1) add(1,1,v[1-(d[x]&1)].size()-1,l1[x],r1[x],-val,1-(d[x]&1)); } else { int x=read(); printf("%d\n",ask(1,1,v[d[x]&1].size()-1,l2[x],d[x]&1)); } } }

牛的,出了381个数据。 考虑有四种情况:一种是只对着两个相邻的攻击,需要max(max(x+1,y+1)/2,(x+y+2)/3)。一种是对着一个攻击,让溅射伤害把相邻的两个打掉,需要max(a[i-1],a[i+1])。一种是先溅射a[i-1]和a[i+1],把最小的溅射掉之后,把打的打掉,需要min(x,y)+(max(x,y)-min(x,y)+1)/2。一种是打两个离得更远的,需要(x+1)/2+(y+1)/2 int ask(int x,int y) { return max(max(x+1,y+1)/2,(x+y+2)/3); } int ask1(int x,int y) { return min(max(x,y),min(x,y)+(max(x,y)-min(x,y)+1)/2); } int n,a[200010],ans; int main() { // freopen("1.in","r",stdin); n=read(); ans=2e6; for(int i=1;i<=n;i++) a[i]=read(); for(int i=2;i<=n;i++) ans=min(ans,ask(a[i],a[i-1])); for(int i=2;i<n;i++) ans=min(ans,ask1(a[i-1],a[i+1])); sort(a+1,a+1+n); ans=min(ans,(a[1]+1)/2+(a[2]+1)/2); cout<<ans; }

注意到ti<t[i+1],r<=500,所以时间大于1000的位置一定可以走过去,所以用这个特性加速dp即可。 int f[100010],n,r,ans[100010]; int t[100010],x[100010],y[100010]; int main() { r=read();n=read(); x[0]=y[0]=1; for(int i=1;i<=n;i++) { t[i]=read();x[i]=read();y[i]=read(); f[i]=-4e6; for(int j=max(0,i-1100);j<i;j++) if(abs(x[i]-x[j])+abs(y[i]-y[j])<=t[i]-t[j]) f[i]=max(f[i],f[j]+1); if(i>=1100) f[i]=max(f[i],ans[i-1100]+1); ans[i]=max(ans[i-1],f[i]); } printf("%d",ans[n]); }

简单dp 注意到h最大不到900,可以fi表示用i个红色块拼前几层中的某几层的方案数,答案即为i+g大于等于所需数量的f[i]的和。 int r,g,h; int f[300000],ans,mod=1e9+7; int main() { r=read();g=read(); for(h=1;;h++) if((1+h)*h/2>r+g) break; h--; f[0]=1; for(int i=1;i<=h;i++) for(int j=r;j>=i;j--) f[j]=(f[j]+f[j-i])%mod; for(int i=0;i<=r;i++)// if(i+g>=(1+h)*h/2) ans=(ans+f[i])%mod; cout<<ans; }

刚开始想了个贪心:对于multiset里的最小的数字x给他匹配lower_bound(x+z)。但是这是不太对的,比如 4 2 1 3 4 5 如果把3给了1,那么45就不能匹配了。但是如果1和4匹配,3和5匹配则皆大欢喜。 那么考虑另一个贪心:二分答案x,然后贪心的让前x和后x个进行匹配,如果不满足条件则一定不行。 int n,z,a[200010]; int check(int x) { for(int l=1,r=n-x+1;r<=n;l++,r++) if(a[l]+z>a[r]) return 0; return 1; } int main() { // freopen("1.in","r",stdin); n=read();z=read(); for(int i=1;i<=n;i++) a[i]=read(); sort(a+1,a+1+n); int l=0,r=n/2,mid; while(l+1<r) { mid=(l+r)/2; if(check(mid)) l=mid; else r=mid; } if(check(r)) printf("%d",r); else printf("%d",l); }

考虑targan找桥,如果有桥输出0。因为原图连通,所以跑一次targan(1,0)即可。 对于输出边,考虑把第一次访问到每个点的那个边输出出来,也就是搜索树上的边。其他的边只要dfn[x]>dfn[y]的那个方向。 int tot,head[100010],dfn[100010],low[100010],n,m,num; struct edge { int x,y,next; }e[600010]; int flag[600010]; void add(int x,int y) { tot++; e[tot].x=x; e[tot].y=y; e[tot].next=head[x]; head[x]=tot; } void tarjan(int x,int in_) { dfn[x]=low[x]=++num; for(int i=head[x];i;i=e[i].next) { int y=e[i].y; if(!dfn[y]) { flag[i]=1;//需要被输出 tarjan(y,i); low[x]=min(low[x],low[y]); if(low[y]>dfn[x]) { printf("0"); exit(0); } } else if(i!=(in_^1)) low[x]=min(low[x],dfn[y]); } } int main() { // freopen("1.in","r",stdin); n=read();m=read(); tot=1; for(int i=1;i<=m;i++) { int x=read(),y=read(); add(x,y); add(y,x); } tarjan(1,0); for(int i=2;i<=tot;i++) { if(flag[i]) printf("%d %d\n",e[i].x,e[i].y); else if(flag[i^1]==0&&dfn[e[i].x]>dfn[e[i].y]) printf("%d %d\n",e[i].x,e[i].y); } }

基环树,考虑容斥。 普通的两个点之间都有两条路径,一条只经过树边,另一条经过多出来的那一条边。 注意到基环树上的点向外的那个子树,内部取两个点并不存在 经过那条边的路径,所以答案减去siz*(siz-1)/2。 int siz[200010]; vector<int>e[200010]; int n,fa[200010],vis[200010],d[200010]; void dfs(int x) { siz[x]=1; for(auto y:e[x]) { if(fa[y])continue; fa[y]=x; d[y]=d[x]+1; dfs(y); siz[x]+=siz[y]; } } int ask(int x) { int sum=1; vis[x]=1; for(auto y:e[x]) if(vis[y]==0) sum=sum+ask(y); return sum; } void work() { n=read(); for(int i=1;i<=n;i++) { e[i].clear(); fa[i]=0; d[i]=0; vis[i]=0; } fa[1]=-1; for(int i=1;i<=n;i++) { int x=read();int y=read(); e[x].push_back(y); e[y].push_back(x); } dfs(1); for(int x=1;x<=n;x++) { for(auto y:e[x]) if(y!=fa[x]&&fa[y]!=x) { int tx=x,ty=y; while(d[tx]<d[ty]) { ty=fa[ty]; vis[ty]=1; } while(d[ty]<d[tx]) { tx=fa[tx]; vis[tx]=1; } while(tx!=ty) { tx=fa[tx]; ty=fa[ty]; vis[tx]=vis[ty]=1; } vis[x]=vis[y]=1; x=n+1; break; } } ll ans=1ll*n*(n-1); for(int i=1;i<=n;i++) if(vis[i]) { ll sum=ask(i); ans=ans-sum*(sum-1)/2; } printf("%lld\n",ans); } int main() { freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

问题就是求每个点x到pi的最远距离,如果最远距离小于等于d就ans++,所以考虑换根dp。 首先一遍dfs处理处f[x]表示x到儿子的最远距离,包括自己的,然后本来这里需要记录最大值和次大值的,我用了vector。然后考虑再来一遍dfs,记录一下从父亲来的非儿子的最远距离now,那么最远距离就是f[x]的最大值和now取max。那么now的转移过程就是,如果f[x]是从儿子y过来的,那么给儿子y次大值或者now取max,如果不是就送给儿子最大值和now取max。 int flag[100010],siz[100010]; int n,m,d,fa[100010],ans; vector<int>f[100010],e[100010]; void dfs(int x) { if(flag[x]) f[x].push_back(0); else f[x].push_back(-1e9); for(auto y:e[x]) { if(y==fa[x])continue; fa[y]=x; dfs(y); f[x].push_back(f[y][siz[y]-1]+1); } sort(f[x].begin(),f[x].end()); siz[x]=f[x].size(); } void dfs1(int x,int now) { if(now<=d&&f[x][siz[x]-1]<=d) ans++; for(auto y:e[x]) { if(y==fa[x])continue; if(f[y][siz[y]-1]+1==f[x][siz[x]-1])//最大值是从儿子来的 dfs1(y,max(now,f[x][siz[x]-2])+1); else dfs1(y,max(now,f[x][siz[x]-1])+1); } } void work() { n=read();m=read();d=read(); for(int i=1;i<=m;i++) flag[read()]=1; for(int i=1;i<n;i++) { int x=read(),y=read(); e[x].push_back(y); e[y].push_back(x); } dfs(1); dfs1(1,-1e9); printf("%d\n",ans); } int main() { // freopen("1.in","r",stdin); // for(int t=read();t;t--) work(); }

注意到数字最多六七次就会变成D(x)=x的状态,所以考虑暴力地树状数组修改区间和,如果已经变成D(x)=x的话就从此不再修改了,复杂度n*6*logn。区间询问直接树状数组即可。预处理D[x]可以用调和级数发现复杂度为nlogn int lowbit(int n) { return n&(-n); } int nex[1000010],n,m,now[1000010]; ll c[1000010]; set<int>o; void add(int x,int d) { while(x<=n) { c[x]+=d; x=x+lowbit(x); } } ll ask(int l,int r) { ll sum=0; while(r) { sum=sum+c[r]; r=r-lowbit(r); } l--; while(l) { sum=sum-c[l]; l=l-lowbit(l); } return sum; } int main() { // freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++) { int x=read(); add(i,x); o.insert(i); now[i]=x; } for(int i=1;i<=1000000;i++) for(int j=i;j<=1000000;j+=i) nex[j]++; for(int i=1;i<=m;i++) { if(read()&1) { int l=read(); int r=read(); if(o.size()&&*o.rbegin()>=l) { for(set<int>::iterator t=o.lower_bound(l);t!=o.end()&&*t<=r;) { int pos=*t; t++; if(nex[now[pos]]==now[pos])//如果没变 o.erase(o.find(pos)); else { add(pos,-now[pos]); add(pos,nex[now[pos]]); now[pos]=nex[now[pos]]; } } } } else { int l=read(); int r=read(); printf("%lld\n",ask(l,r)); } } }

首先注意到bi只可能买某一种的bi,不可能买几个b1买几个b2,所以第一步是枚举买哪个bi,那么ai是必买的,其他的aj的话,如果大于bi的话可以买,如果小于bi就不买了。所以枚举i,二分查找买几个aj。 细节有点多,写了好久 ll n,m; ll a[100010],b[100010],t[100010],c[100010]; ll ans; ll solve(ll v1,ll v) { if(v>t[m]) return v1+v*(n-1); ll pos=lower_bound(t+1,t+1+m,v)-t; pos=max(pos,m-n+2); if(v1>=t[pos]) return c[pos]+v*(n-m+pos-1); else return c[pos]+v1+v*(n-m+pos-2); } void work() { n=read();m=read(); for(int i=1;i<=m;i++) t[i]=a[i]=read(),b[i]=read(); sort(t+1,t+1+m); c[m+1]=0; for(int i=m;i>=0;i--) c[i]=c[i+1]+t[i]; if(n>=m) ans=c[1]; else ans=c[m-n+1]; for(int i=1;i<=m;i++) ans=max(ans,solve(a[i],b[i])); printf("%lld\n",ans); } int main() { // freopen("1.in","r",stdin); // freopen("2.out","w",stdout); for(int t=read();t;t--) work(); }

考虑树dp 对于白点,$f[x][0]$表示允许x的白点连通块还没有归属的方案数,$f[x][1]$表示全部已经有归属了的方案数 $f[x][0]=\prod (f[y][1]+f[y][0])$ 如果已经有归属了就不连边,否则连边 $f[x][1]=\sum f[z][1]* \prod (f[y][0]+f[y][1])$ 找一个已有归属的点连边,其他的如果已有归属了可不边边+如果没有归属连边 对于黑点,只允许$f[x][1]$表示方案数 $f[x][1]=\prod (f[y][1]+f[y][0])$ 如果y已经有归属了,就不连边,否则连边 ll mod=1000000007; ll quick(ll a,ll b) { ll t=1; while(b) { if(b&1) t=t*a%mod; a=a*a%mod; b=b>>1; } return t; } int n,a[100010]; ll f[100010][2]; vector<int>e[100010]; void dfs(int x) { for(auto y:e[x]) dfs(y); if(a[x]==1) { f[x][1]=1; for(auto y:e[x]) f[x][1]=f[x][1]*(f[y][1]+f[y][0])%mod; } else { f[x][0]=1; for(auto y:e[x]) f[x][0]=f[x][0]*(f[y][0]+f[y][1])%mod; for(auto y:e[x]) f[x][1]=(f[x][1]+f[x][0]*quick(f[y][0]+f[y][1],mod-2)%mod*f[y][1])%mod; } } int main() { // freopen("1.in","r",stdin); n=read()-1; for(int i=1;i<=n;i++) e[read()].push_back(i); for(int i=0;i<=n;i++) a[i]=read(); dfs(0); printf("%lld",f[0][1]); }

注意到每次做修改操作,数组的max是单调不增的 那么考虑如果最大值的左边有至少两个位置或者右边有至少两个位置,就可以做出来0,进而把区间都变成最大值,对应着n>=4的情况 而对于n=1、n=2、n=3暴力的枚举即可。 int n; ll a[200010]; void work() { n=read(); for(int i=1;i<=n;i++) a[i]=read(); if(n>=4) { sort(a+1,a+1+n); printf("%lld\n",n*a[n]); return ; } if(n==1) printf("%lld\n",a[1]); else if(n==2) printf("%lld\n",max(2*abs(a[1]-a[2]),a[1]+a[2])); else { ll ans=a[1]+a[2]+a[3]; ans=max(ans,3*abs(a[1]-a[3]));//1 3 ans=max(ans,2*abs(a[1]-a[2])+a[3]);// 1 2 ans=max(ans,2*abs(a[3]-a[2])+a[1]);//2 3 ans=max(ans,3*abs(a[1]-abs(a[2]-a[3])));//2 3,1 3 ans=max(ans,3*abs(a[3]-abs(a[1]-a[2])));//1 2,1 3 ans=max(ans,3*a[1]);//2 3,2 3,1 3 ans=max(ans,3*a[3]);//1 2,1 2,1 3 ans=max(ans,3*abs(a[2]-a[3]));//2 3,1 2,1 2,1 3 ans=max(ans,3*abs(a[1]-a[2]));//1 2,2 3,2 3,1 3 printf("%lld\n",ans); } } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

哎呀被虐了 想了半天线段树模拟字典树,但是代码实现方面发现好像需要nlog^3,难顶。看了题解才得知这么简单。 考虑bi表示ai的最大的1所在的位置,因为ai<=a[i+1],所以有bi<=b[i+1]。 那么如果存在b[i-1]==bi==b[i+1],就可以通过让i和i+1异或一下达成目的。 如果不存在,证明bi数组递增,又因为ai的范围只有10^9,所以n的范围只会有30左右,此时可以n^3暴力。 int ask(int x) { int sum=0; while(x) { x=x/2; sum++; } return sum; } int n,ans,a[100010],b[100010],c[100010]; void work() { n=read(); ans=3*n; for(int i=1;i<=n;i++) { a[i]=read(); b[i]=ask(a[i]); c[i]=c[i-1]^a[i]; } for(int i=3;i<=n;i++) { if(b[i-2]==b[i-1]&&b[i-1]==b[i]) { printf("1\n"); return ; } } for(int l=1;l<=n;l++) for(int r=l;r<=n;r++) for(int tl=r+1,tr=tl;tr<=n;tr++) if((c[r]^c[l-1])>(c[tr]^c[tl-1])) ans=min(ans,tr-tl+r-l); if(ans==3*n) printf("-1\n"); else printf("%d\n",ans); } int main() { // freopen("1.in","r",stdin); // for(int t=read();t;t--) work(); }

令a、ab、abc是到i位置的a、ab、abc的数量,sum记录3^问号出现的次数。那么如果s[i]=='a',那么这个位置对于问号的每种选择方式都会贡献一次1的贡献,所以a=a+sum。如果是b或c则简单一点,+=a和+=ab即可。 如果这里是问号,那么这里选三种情况会使得a、ab、abc变成三倍,并且分别考虑这里选a还是b还是c会对a、ab、abc的贡献,最后把sum*3即可 ll mod=1e9+7,a,ab,abc,n,sum=1; char s[200010]; void work() { n=read(); scanf("%s",s); for(int i=0;i<n;i++) { if(s[i]=='a') a=(a+sum)%mod; else if(s[i]=='b') ab=(ab+a)%mod; else if(s[i]=='c') abc=(abc+ab)%mod; else { abc=(abc*3+ab)%mod; ab=(ab*3+a)%mod; a=(a*3+sum)%mod; sum=sum*3%mod; } } cout<<abc; } int main() { // freopen("1.in","r",stdin); // for(int t=read();t;t--) work(); }

首选两个点为直径的端点 第三个点从直径上的点出发bfs,选择距离最远的那个 答案即为直径长度+第三个点到直径的最短距离 int maxx,vis[200010],pre[200010],n,l,r,ans,d[200010]; vector<int>e[200010]; queue<int>q; void dfs(int x,int d) { if(d>maxx) maxx=d,l=x; vis[x]=1; for(auto y:e[x]) { if(!vis[y]){ pre[y]=x; dfs(y,d+1); } } vis[x]=0; } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<n;i++) { int x=read(),y=read(); e[x].push_back(y); e[y].push_back(x); } maxx=0; dfs(1,1); maxx=0; r=l; dfs(r,1); if(maxx==n) for(int i=1;i<=n;i++) { if(i!=l&&r!=i) { cout<<n-1<<' '<<l<<' '<<r<<' '<<i<<endl; return 0; } } else { memset(d,-1,sizeof(d)); int x=l; while(x!=r) { q.push(x); d[x]=0; x=pre[x]; } ans=q.size(); d[r]=0; q.push(r); while(q.size()) { x=q.front();q.pop(); for(auto y:e[x]) if(d[y]==-1) { d[y]=d[x]+1; q.push(y); } } x=1; for(int i=1;i<=n;i++) if(d[i]>d[x]) x=i; cout<<ans+d[x]<<endl<<l<<' '<<r<<' '<<x; } }

考虑spfa跑最短路 最坏情况下也就跑到2n再拐回来 所以设立一个上界即可 spfa真牛 int n; long long x,y,d[20000010]; queue<int>q; int vis[20000010]; int main() { n=read();x=read();y=read(); for(int i=1;i<=2*n;i++) d[i]=x*i+1; q.push(0); while(q.size()) { int tx=q.front(); q.pop(); vis[tx]=0; if(tx!=2*n&&d[tx]+x<d[tx+1]) { d[tx+1]=d[tx]+x; if(vis[tx+1]==0) { vis[tx+1]=1; q.push(tx+1); } } if(tx!=0&&d[tx]+x<d[tx-1]) { d[tx-1]=d[tx]+x; if(vis[tx-1]==0) { vis[tx-1]=1; q.push(tx-1); } } if(tx<=n&&d[tx]+y<d[tx*2]) { d[tx*2]=d[tx]+y; if(vis[tx*2]==0) { vis[tx*2]=1; q.push(tx*2); } } } cout<<d[n]; }

能够被逼到L当且仅当只有一个出路且这个出路能够被逼到L,或者只有两个出路,并且其中一个能够被逼到L 所以大胆bfs,类似拓扑排序 int n,m,sum,dx[]={0,0,1,-1},dy[]={1,-1,0,0}; string s[1000010]; queue<pair<int,int>>q; int check(int tx,int ty) { if(tx*ty!=0&&tx<=n&&ty<=m&&s[tx][ty]=='.') { sum=0; for(int kk=0;kk<4;kk++) if((tx+dx[kk])*(ty+dy[kk])!=0&&tx+dx[kk]<=n&&ty+dy[kk]<=m) sum=sum+(s[tx+dx[kk]][ty+dy[kk]]=='.'); if(sum<=1) return 1; } return 0; } void work() { n=read();m=read(); for(int i=1;i<=n;i++){ cin>>s[i]; s[i]='0'+s[i]; } for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { if(s[i][j]=='L') { for(int k=0;k<4;k++) { int tx=i+dx[k]; int ty=j+dy[k]; if(check(tx,ty)) { q.push({tx,ty}); s[tx][ty]='+'; } } } } } while(q.size()) { int tx=q.front().first; int ty=q.front().second; q.pop(); for(int i=0;i<4;i++) if(check(tx+dx[i],ty+dy[i])) { s[tx+dx[i]][ty+dy[i]]='+'; q.push({tx+dx[i],ty+dy[i]}); } } for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) printf("%c",s[i][j]); printf("\n"); } } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

考虑最短路有哪几种情况 要么a走树边走到b 要么a走树边到x,再走新加的边走到y,再走树边走到b 要么a走树边到y,再走新加的边走到x,再走树边走到b 检查这三个方案的最短路是否小于等于k且奇偶性相同即可 vector<int>e[100010]; int n,d[100010],f[100010][30]; void dfs(int x) { for(auto y:e[x]) { if(y==f[x][0])continue; d[y]=d[x]+1; f[y][0]=x; dfs(y); } } int lca(int x,int y) { int ttt=d[x]+d[y]; if(d[x]>d[y]) swap(x,y); for(int i=20;i>=0;i--) if(d[f[y][i]]>=d[x]) y=f[y][i]; if(x==y) return ttt-2*d[x]; for(int i=20;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; return ttt-2*d[f[x][0]]; } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<n;i++) { int x=read();int y=read(); e[x].push_back(y); e[y].push_back(x); } d[1]=1; dfs(1); for(int i=1;i<=20;i++) { for(int x=1;x<=n;x++) f[x][i]=f[f[x][i-1]][i-1]; } for(int q=read();q;q--) { int x=read(),y=read(),a=read(),b=read(); int k=read(); int Dab=lca(a,b),Daxyb=lca(a,x)+1+lca(b,y),Dayxb=lca(a,y)+1+lca(x,b); if(Dab<=k&&Dab%2==k%2||Daxyb<=k&&Daxyb%2==k%2||Dayxb<=k&&Dayxb%2==k%2) printf("YES\n"); else printf("NO\n"); } }

考虑二分长度,然后枚举所有该长度的子串,如果满足要求就返回1,否则返回0 那么对于l,r,如何判断是否存在aj使得所有数字整除aj呢 只需要看看区间gcd是否整除最小的aj即可。区间gcd和区间最小值都可以线段树搞一搞 复杂度nlog^2 int minn[1200010],gcd[1200010],a[300010]; int n; void build(int x,int l,int r) { if(l==r) { minn[x]=a[l]; gcd[x]=a[l]; return ; } int mid=(l+r)/2; build(x*2,l,mid); build(x*2+1,mid+1,r); minn[x]=min(minn[x*2],minn[x*2+1]); gcd[x]=__gcd(gcd[x*2],gcd[x*2+1]); } pair<int,int>ask(int x,int l,int r,int tl,int tr) { if(tl<=l&&r<=tr) return {minn[x],gcd[x]}; int mid=(l+r)/2; pair<int,int>lll,rrr; if(tr<=mid) return ask(x*2,l,mid,tl,tr); else if(tl>mid) return ask(x*2+1,mid+1,r,tl,tr); else { lll=ask(x*2,l,mid,tl,tr); rrr=ask(x*2+1,mid+1,r,tl,tr); return {min(lll.first,rrr.first),__gcd(lll.second,rrr.second)}; } } int check(int len) { for(int l=1,r=len+1;r<=n;l++,r++) { pair<int,int> t =ask(1,1,n,l,r); if(t.second%t.first==0) return 1; } return 0; } void print(int len) { queue<int>q; for(int l=1,r=len+1;r<=n;l++,r++) { pair<int,int> t =ask(1,1,n,l,r); if(t.second%t.first==0) q.push(l); } printf("%d %d\n",q.size(),len); while(q.size()) { printf("%d ",q.front()); q.pop(); } } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) a[i]=read(); build(1,1,n); int l=0,r=n-1,mid; while(l+1<r) { mid=(l+r)/2; if(check(mid)) l=mid; else r=mid; } if(check(r)) print(r); else print(l); }

可以发现只要是左右端点相同的子串都是满足要求的”回文串“ 那么就看如何统计答案了 长为偶数的串的数量为位于奇数位置上的'a'的数量*位于偶数位置上的'a'的数量+奇数位置上的'b'的数量*位于偶数位置上的'b'的数量 长为奇数的串的数量与之类似 char s[100010]; int n; ll ans,sum[300][2]; int main() { scanf("%s",s); n=strlen(s); for(int i=0;i<n;i++) sum[s[i]][i&1]++; ans+=sum['a'][0]*sum['a'][1]; ans+=sum['b'][0]*sum['b'][1]; printf("%lld ",ans); ans=0; ans+=(sum['a'][0]+1)*sum['a'][0]; ans+=(sum['a'][1]+1)*sum['a'][1]; ans+=(sum['b'][0]+1)*sum['b'][0]; ans+=(sum['b'][1]+1)*sum['b'][1]; ans=ans/2; printf("%lld",ans); }

首先跑一个动态规划,f[i]表示要删掉i个数字,能用操作1也能用操作2所需要的最少花费(注意这里有可能只用操作1或者只用操作2 那么考虑如果只能用操作2,当且仅当要删的区间最大值小于区间两个端点的最大值 如果既用操作1也用操作2,那么需要区间长度大于等于k 理清逻辑后可以发现: 1、如果区间最大值小于端点最大值,那么随意怎么用操作12,所以直接使用预处理出来的最小花费即可 2、如果区间最大值大于端点最大值且长度大于等于k,那么只需确保最后一次操作使用的是操作1(也就是要求至少使用一次操作1),这个要求可以使用x+f[len-k]来得到 3、如果区间最大值大于端点最大值且长度小于k,那么只能使用操作2,并且删不完,所以输出-1 int n,m,x,y,k,l,r,v[200010],pos[200010],b[200010]; ll f[200010],maxx,ans,a[200010]; queue<int>q; void print() { printf("-1"); exit(0); } int main() { // freopen("1.in","r",stdin); n=read();m=read(); x=read();k=read();y=read(); memset(f,0x3f,sizeof(f)); f[0]=0; for(int i=1;i<=n;i++) { if(i>=k) f[i]=min(f[i-1]+y,f[i-k]+x); else f[i]=y*i; } for(int i=1;i<=n;i++) a[i]=read(); for(int i=1;i<=m;i++) b[i]=read(),q.push(b[i]); for(int i=1;i<=n;i++) { if(q.size()&&a[i]==q.front()) q.pop(),v[i]=m-q.size(); } if(q.size()) print(); for(int i=1;i<=n;i++) pos[v[i]]=i; if(pos[1]>1) { maxx=0; for(int i=1;i<pos[1];i++) maxx=max(maxx,a[i]); if(b[1]>maxx) ans=ans+f[pos[1]-1]; else if(pos[1]-1>=k) ans=ans+f[pos[1]-1-k]+x; else print(); } if(pos[m]<n) { maxx=0; for(int i=pos[m]+1;i<=n;i++) maxx=max(maxx,a[i]); if(b[m]>maxx) ans=ans+f[n-pos[m]]; else if(n-pos[m]>=k) ans=ans+f[n-pos[m]-k]+x; else print(); } for(int i=1;i<m;i++) { l=pos[i],r=pos[i+1]; maxx=0; for(int j=l+1;j<r;j++) maxx=max(maxx,a[j]); if(maxx<max(a[l],a[r])) ans+=f[r-l-1]; else if(r-l-1>=k) ans+=f[r-l-1-k]+x; else print(); } printf("%lld",ans); }

首先观察样例大胆猜测答案是单调递减子序列长度 然后进行dp int n,f[200010],maxf[300],ans; char s[200010]; int main() { n=read(); scanf("%s",s); for(int i=0;i<n;i++) { f[i]=1; for(int j='z';j>s[i];j--) f[i]=max(f[i],maxf[j]+1); maxf[s[i]]=max(maxf[s[i]],f[i]); } for(int i=0;i<n;i++) ans=max(ans,f[i]); printf("%d\n",ans); for(int i=0;i<n;i++) printf("%d ",f[i]); }

考虑优雅的暴力 如果刚开始ab都大于sqrt(6n) 那么答案的ab不会改变 否则答案里ab至少有一个数字小于等于sqrt(6n)(有可能两个都等于) 那么枚举这个答案即可 ll n,a,b,ans,aa,bb; void ask(ll a1,ll b1) { if(a1*b1<ans) ans=a1*b1,aa=a1,bb=b1; } int main() { n=read()*6ll;a=read();b=read(); ans=2e18; for(ll x=1;x*x<=n;x++) { ask(max(a,x),max(b,(n+max(a,x)-1)/max(a,x))); ask(max(a,(n+max(b,x)-1)/max(b,x)),max(b,x)); } printf("%lld\n%lld %lld",ans,aa,bb); }

今天重新认识了一下dij,T了半天发现我dij的写法一直有错 考虑建立一个超级源点0,0->x连边长为ai的边 然后对于原图的x->y长度为w,连x->y长度为2w 那么跑出来的0到达x的最短路,假如第一步走的是y,就等于原图里x去y看演出花费最小,花费等于0到x的最短路 int n; struct edge { int y,next; ll w; }e[600010]; int head[200010],tot,v[200010]; ll d[200010]; priority_queue<pair<ll,int>>q; void add(int x,int y,ll w) { tot++; e[tot].y=y; e[tot].next=head[x]; e[tot].w=w; head[x]=tot; } int main() { // freopen("1.in","r",stdin); n=read(); for(int m=read();m;m--) { int x=read();int y=read(); ll tw=read()*2; add(x,y,tw); add(y,x,tw); } for(int i=1;i<=n;i++) add(0,i,read()); for(int i=1;i<=n;i++) d[i]=1e18; d[0]=0; q.push({0,0}); while(q.size()) { int x=q.top().second; q.pop(); if(v[x]) continue; v[x]=1; for(int i=head[x];i;i=e[i].next) { if(d[e[i].y]>d[x]+e[i].w) { d[e[i].y]=d[x]+e[i].w; q.push({-d[e[i].y],e[i].y}); } } } for(int i=1;i<=n;i++) printf("%lld ",d[i]); }

克鲁斯卡尔 枚举当前边权最小的”边“,看看最远能扩展到哪 然后并查集 int n,p,a[200010],fa[200010],l,r; ll ans; priority_queue<pair<int,int>>q; int get(int x) { return fa[x]==x?x:fa[x]=get(fa[x]); } void work() { n=read();p=read();ans=0; for(int i=1;i<=n;i++) { a[i]=read(); q.push({-a[i],i}); fa[i]=i; } fa[n+1]=0; while(q.size()&&-q.top().first<p) { int pos=q.top().second,l,r;q.pop(); l=r=pos; while(l!=1&&get(l-1)!=get(pos)&&a[l-1]%a[pos]==0) { l--; fa[fa[l]]=fa[pos]; ans=ans+a[pos]; } while(r!=n&&get(r+1)!=get(pos)&&a[r+1]%a[pos]==0) { r++; fa[fa[r]]=fa[pos]; ans=ans+a[pos]; } } for(int i=2;i<=n;i++) if(get(i)!=get(i-1)) { ans=ans+p; fa[fa[i]]=fa[i-1]; } printf("%lld\n",ans); while(q.size()) q.pop(); } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

一眼二分答案 那么统计答案时 考虑最终数字所在的区间,假设左端点位于a[l]和a[l+1]之间,右端点位于a[r]和a[r+1]之间,如果需要减小的数字的数量等于需要增大的数字的数量,那么这个区间可以在有限的范围里平移。如果一边多,那么一定是左端点位于某个ai或者右端点位于某个ai上的 综上,二分答案v,枚举左端点位于ai和右端点位于ai的情况,计算最小花费,return 最小花费<=k即可 ll k,a[100010],c[100010],n; int check(int v) { ll sum=1e16; for(int l=1,r=1;l<=n;l++)//以a[l]为左端点,a[l]+v为右端点 { while(r!=n+1&&a[r]<=a[l]+v) r++;//r表示第一个需要变小的值 sum=min(sum,a[l]*l-c[l]+c[n]-c[r-1]-(a[l]+v)*(n+1-r)); } for(int r=n,l=n;r;r--)//以a[r]-v为左端点,a[r]为右端点 { while(l!=0&&a[l]>=a[r]-v) l--; sum=min(sum,(a[r]-v)*l-c[l]+c[n]-c[r-1]-a[r]*(n+1-r)); } return sum<=k; } int main() { n=read();k=read(); for(int i=1;i<=n;i++) a[i]=read(); sort(a+1,a+1+n); for(int i=1;i<=n;i++) c[i]=c[i-1]+a[i]; int l=0,r=a[n]-a[1],mid; while(l+1<r) { mid=(l+r)/2; if(check(mid)) r=mid; else l=mid; } if(check(l)) printf("%d",l); else printf("%d",r); }

模拟 首先显然应该判断一下n是否%k==0 其次检查一下原串是否满足条件 如果不行就要考虑严格大于原串的最小字典序 可以从后往前枚举把这一位变成多少,那么O(26)地检查一下能否得到满足条件的串,如果可以,就O(nlogn)地构造出答案串(这里可以写成On的) 一套想下来很顺 char s[100010]; int n,k,c[300]; priority_queue<char,vector<char>,greater<char>>q; int check(int x) { if(x==0) { for(int i='a';i<='z';i++) if(c[i]%k!=0) return 0; return 1; } else { int nn=n; for(int i='a';i<='z';i++) { if(c[i]%k!=0) nn=nn-k+c[i]%k; nn=nn-c[i]; } return nn>=0; } } void print(int pos) { for(int i=0;i<=pos;i++) printf("%c",s[i]); for(int i='a';i<='z';i++) while(c[i]%k!=0) { q.push(i); c[i]++; } while(q.size()<n-pos-1) q.push('a'); for(int i=pos+1;i<n;i++) { printf("%c",q.top()); q.pop(); } printf("\n"); } void work() { scanf("%d%d%s",&n,&k,s); if(n%k!=0) { printf("-1\n"); return ; } for(int i='a';i<='z';i++) c[i]=0; for(int i=0;i<n;i++) c[s[i]]++; if(check(0)) { printf("%s\n",s); return ; } for(int i=n-1;i>=0;i--) { c[s[i]]--;//先把本位-- for(s[i]++;s[i]<='z';s[i]++)//枚举新的本位 { c[s[i]]++; if(check(1)) { print(i); return ; } c[s[i]]--; } } printf("-1\n"); return ; } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

首先可以想到的是,任意长为2的相邻元素之和应该大于等于2x 这并不充分,应为x=3,2 4 2 满足长为2的和大于等于2x,但是长为3的和并不大于等于3x 那么进一步考虑,如果任意长为2的满足且长为3的满足,那么就可以满足所有的区间平均数大于等于x 然后考虑贪心地选即可 int n,a[50010],x,f[50010],ans; void work() { n=read();ans=0; for(int i=1;i<=n;i++) a[i]=read(); x=read(); for(int i=1;i<=n;i++) { if(i>=3&&f[i-1]&&f[i-2]&&a[i]+a[i-1]+a[i-2]<3*x||i>=2&&f[i-1]&&a[i]+a[i-1]<2*x) f[i]=0; else f[i]=1,ans++; } printf("%d\n",ans); } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

大胆谈心 首先,如果当前存在数字每一位之和大于1也就是不为10^k,可以考虑把它拆分成两个数字而不改变十一进制下的和 如果全是10^k,例如有1,10,100,1000,可以发现1拆不了,可以把非1的最小的10^k拆成10^(k-1)和9*10^(k-1),例如上个例子中,10拆成1和9是最优秀的 vector<int>o; int n; void work() { for(int i=0;i<o.size();i++) { int x=log10(o[i]); if(pow(10,x)==o[i]) continue; else for(int j=1;j<=o[i];j=j*10) { if((o[i]/j)%10!=0){ o.push_back(j); o[i]-=j; return ; } } } sort(o.begin(),o.end()); for(int i=0;i<o.size();i++) { if(o[i]!=1) { o.push_back(o[i]/10); o[i]=o.back()*9; break; } } } void solve() { o.clear(); o.push_back(read());n=read(); for(int i=2;i<=n;i++) work(); for(auto x:o) printf("%d ",x); printf("\n"); } int main() { for(int t=read();t;t--) solve(); }

状压DP 考虑bi最多跑到59,再大就不如直接跑到1了 并且一定有解,因为可以都变成1 那么预处理出质数,然后预处理出每个数字含有质数的情况(用状态压缩) 然后开始dp,f[i][j]记录前i个数字,用质因数的情况是j的最小花费。pre[i][j]记录该情况下bi等于几。 最后逆着还原现场 int prime[]={2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53}; int sum=sizeof(prime)/4; int v[100],a[110];//记录含有质因数的情况和原数组 int f[110][100000],n,pre[110][100000],ans;/ stack<int>q; int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) a[i]=read(); for(int i=1;i<=60;i++) for(int j=0;j<sum;j++) if(i%prime[j]==0) v[i]|=(1<<j); memset(f,0x3f,sizeof(f)); f[0][0]=0; for(int i=1;i<=n;i++) { for(int x=1;x<=60;x++) { for(int k=0;k<(1<<sum);k++) if(((k&v[x])==0)&&f[i][k|v[x]]>f[i-1][k]+abs(a[i]-x)) { f[i][k|v[x]]=f[i-1][k]+abs(a[i]-x); pre[i][k|v[x]]=x; } } } ans=0; for(int i=0;i<(1<<sum);i++) if(f[n][i]<f[n][ans]) ans=i; for(int i=n;i>=1;i--) { q.push(pre[i][ans]); ans=ans^(v[pre[i][ans]]); } while(q.size()) { printf("%d ",q.top()); q.pop(); } }

唉我真疯了一个傻逼错误查半天就差跪下来求求cf告诉我错哪了 考虑如果存在i到j等于j到i,那么直接在ij之间来回跑就行 如果不存在,证明任意ij,i到j不等于j到i 那么如果m是奇数,也可以任意找一对ij来回跑 现在面临着m是偶数且任意ij,i到j不等于j到i 那么如果n等于2的话,就只能构造出abab或者baba,就寄了 否则考虑1 2 3 这个三角形,顺着1 2 3 的方向看 如果三条边一样,那么顺着这个三角形跑即可 如果不一样,那么一定是两个一样的+一个不同的 不妨假设是aab 那么如果m%4==0 可以构造出abba abba abba循环 如果m%4==2 可以构造出aa后面bbaa 循环 int n,m,beg; char s[1010][1010]; void work() { n=read();m=read(); for(int i=1;i<=n;i++) scanf("%s",s[i]+1); for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) if(s[i][j]==s[j][i])//存在aa或者bb的情况,直接输出 { printf("YES\n"); for(int k=1;k<=m+1;k++) { if(k&1) printf("%d ",i); else printf("%d ",j); } printf("\n"); return ; } //接下来就是全是ab的情况 if(m&1) { printf("YES\n"); for(int i=1;i<=m+1;i++) if(i&1) printf("1 "); else printf("2 "); printf("\n"); return ; } if(n==2)//只有一条ab { printf("NO\n"); return ; } printf("YES\n"); if(s[1][2]==s[2][3]&&s[2][3]==s[3][1])//aaa或者bbb { for(int i=1;i<=m+1;i++) printf("%d ",i%3+1); printf("\n"); return ; } if(s[1][2]==s[3][1]) beg=1; else if(s[2][3]==s[1][2]) beg=2; else beg=3; if(m%4==0) { for(int i=1;i<=m/4;i++) printf("%d %d %d %d ",beg,beg%3+1,beg,(beg+1)%3+1); printf("%d\n",beg); } else if(m%4==2) { for(int i=1;i<=m/4;i++) printf("%d %d %d %d ",(beg+1)%3+1,beg,beg%3+1,beg); printf("%d %d %d\n",(beg+1)%3+1,beg,beg%3+1); } } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

我本来想的是每两个元素用三次得到他们的值,试了半天不太会 那么看了一篇题解https://blog.csdn.net/Gh0st_Lx/article/details/116510824 题解说,先用n/2+2次操作2找到1的位置 然后用n-1次操作1得到剩下每个元素的值 又学到了 int n,pos,a[10010],x; void work() { n=read();pos=0; for(int i=1;i+1<=n;i+=2) { cout<<"? 2 "<<i<<' '<<i+1<<" 1"<<endl; cin>>x; if(x==1) { pos=i; a[i]=1; break; } else if(x==2) { cout<<"? 2 "<<i+1<<' '<<i<<" 1"<<endl; cin>>x; if(x==1) { pos=i+1; a[i+1]=1; break; } } } if(pos==0) a[pos=n]=1; for(int i=1;i<=n;i++) { if(i==pos)continue; cout<<"? 1 "<<pos<<' '<<i<<' '<<n-1<<endl; cin>>a[i]; } cout<<"! "; for(int i=1;i<=n;i++) cout<<a[i]<<' '; cout<<endl; } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

考虑如果一个点,但凡位于一个数量大于1的联通块里,那么就会跟着这个联通块开始变动 如果刚开始不存在大连通块,那么以后就都不会出现大连通块了,并且以后都不会变 如果有,那么会逐渐吞并那些大小为1的连通块 令d[x][y]表示距离x,y最近的连通块的距离 那么如果p是小于等于d[x][y]的,那么他仍然没变动 否则,会变动p-d[x][y]次 ll d[1010][1010]; int a[1010][1010],n,m,t; int dx[]={1,-1,0,0},dy[]={0,0,1,-1}; char s[1010]; queue<pair<int,int>>q; int main() { // freopen("1.in","r",stdin); n=read();m=read();t=read(); for(int i=1;i<=n;i++) { scanf("%s",s+1); for(int j=1;j<=m;j++) a[i][j]=s[j]-'0'; } memset(d,0x3f,sizeof(d)); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) for(int k=0;k<4;k++) if(i+dx[k]>=1&&i+dx[k]<=n&&j+dy[k]>=1&&j+dy[k]<=m&&a[i][j]==a[i+dx[k]][j+dy[k]]) { d[i][j]=0; q.push({i,j}); break; } while(q.size()) { int x=q.front().first; int y=q.front().second; q.pop(); for(int k=0;k<4;k++) if(x+dx[k]>=1&&x+dx[k]<=n&&y+dy[k]>=1&&y+dy[k]<=m) if(a[x+dx[k]][y+dy[k]]==a[x][y]&&d[x+dx[k]][y+dy[k]]>d[x][y]) { d[x+dx[k]][y+dy[k]]=d[x][y]; q.push({x+dx[k],y+dy[k]}); } else if(d[x+dx[k]][y+dy[k]]>d[x][y]+1) { d[x+dx[k]][y+dy[k]]=d[x][y]+1; q.push({x+dx[k],y+dy[k]}); } } for(;t;t--) { int x=read();int y=read();ll p=read(); if(p<=d[x][y]) printf("%d\n",a[x][y]); else printf("%d\n",(a[x][y]^(p-d[x][y]))&1); } }

大胆暴力 考虑每次把前k长的不同的串按序放在vector中 把这些串取出来,后面连上a[i],看看是否重复了。如果重复了就扔掉,否则扔到vector里 然后暴力sort,扔掉k个之后的 进入下一循环 最后看看vector的size是否等于k,如果等于k就统计答案输出,否则输出-1 vector<pair<int,string>>o; char s[110]; string t; int n,k,ans; int main() { // freopen("1.in","r",stdin); n=read(); k=read(); scanf("%s",s); o.push_back({0,""}); for(int i=0;i<n;i++) { int ttt=o.size()-1; for(int j=ttt;j>=0;j--) { if(o[j].first-1>=o[ttt].first) continue; t=o[j].second+s[i]; if(*lower_bound(o.begin(),o.begin()+ttt+1,make_pair(o[j].first-1,t))!=make_pair(o[j].first-1,t)) { o.push_back({o[j].first-1,t}); } } sort(o.begin(),o.end()); while(o.size()>k) o.pop_back(); } if(o.size()==k) { for(auto x:o) ans=ans+n+x.first; printf("%d",ans); } else printf("-1"); }

和上一个题类似 先把全选ci的放进堆里 然后开始循环: 如果状态为1则输出 否则开始枚举这次让哪个ai-- 如果得到的新状态是没在堆里呆过的 那么把他扔到堆里 //-1 不可用但是没在堆里待过 //-2 不可用但是没在堆里待过 //0 可用且没在堆里 //1 可用且在堆里 struct node { vector<int>a; ll sum,hash; friend bool operator <(node a,node b) { return a.sum==b.sum?a.hash<b.hash:a.sum<b.sum; } }t; ll mod=1e9+7,hash,p=200003; priority_queue<node>q; map<ll,int>o; int n,c[10],a[10][200010]; int main() { // freopen("1.in","r",stdin); n=read(); for(int i=0;i<n;i++) { c[i]=read(); for(int j=1;j<=c[i];j++) a[i][j]=read(); } t.a.resize(n); for(int m=read();m;m--) { t.sum=0;t.hash=0; for(int i=0;i<n;i++) { int x=read(); t.a[i]=x; t.hash=(t.hash*p+x)%mod; t.sum+=a[i][x]; } o[t.hash]=-1; } t.sum=0;t.hash=0; for(int i=0;i<n;i++) { t.a[i]=c[i]; t.sum+=a[i][c[i]]; t.hash=(t.hash*p+c[i])%mod; } q.push(t); if(o[t.hash]) o[t.hash]=-2; else o[t.hash]=1; while(q.size()) { t=q.top();q.pop(); if(o[t.hash]==1) { for(int i=0;i<n;i++) printf("%d ",t.a[i]); return 0; } for(int i=0;i<n;i++) { if(t.a[i]!=1) { t.sum=t.sum-a[i][t.a[i]]+a[i][t.a[i]-1]; t.a[i]--; t.hash=0; for(int j=0;j<n;j++) t.hash=(t.hash*p+t.a[j])%mod; if(o[t.hash]==-1) { q.push(t); o[t.hash]=-2; } else if(o[t.hash]==0) { q.push(t); o[t.hash]=1; } t.a[i]++; t.sum=t.sum+a[i][t.a[i]]-a[i][t.a[i]-1]; } } } }

考虑动态规划 f[i][j]表示第i个菜用的是第j款 那么f[i][j]=min(f[i-1][k])+a[i][j] | k,j被允许 所以需要一个单点修改,询问全局最小值的数据结构 他就是set(实测set比线段树慢)#include<bits/stdc++.h> using namespace std; typedef long long ll; int read() { int x;scanf("%d",&x);return x; } int n,c[5],a[5][150010],f[5][150010]; vector<int>no[150010]; multiset<int>minn; int main() { // freopen("1.in","r",stdin); for(int i=1;i<=4;i++) c[i]=read(); for(int i=1;i<=4;i++) for(int j=1;j<=c[i];j++) a[i][j]=read(); for(int i=1;i<=c[1];i++) f[1][i]=a[1][i]; for(int now=2;now<=4;now++) { minn.clear(); for(int i=1;i<=c[now-1];i++) minn.insert(f[now-1][i]); for(int i=1;i<=c[now];i++) no[i].clear();//清空不合法vector for(int m=read();m;m--) { int x=read(); no[read()].push_back(x); } for(int i=1;i<=c[now];i++) { for(auto x:no[i]) minn.erase(minn.find(f[now-1][x])); if(minn.empty()) f[now][i]=1e9; else f[now][i]=a[now][i]+*minn.begin(); for(auto x:no[i]) minn.insert(f[now-1][x]); } } int ans=f[4][1]; for(int i=1;i<=c[4];i++) ans=min(ans,f[4][i]); if(ans>=1e9) printf("-1"); else printf("%d",ans); }

算错复杂度了,纠结半天 但实际上就是f[i][j]表示只用1到i,质数用的状态是j的方案数 j&(1<<k)为1就是说用了奇数个第k个质数 为0就是说用了偶数个第k个质数 那么最后答案是f[70][0]表示用了1到70,状态为0也就是平方数的方案数 -1是删去全都不用的这一方案 如果sum[i]==0也就是没有数字i,那么f[i][j]=f[i-1][j]继承 否则考虑得到数字i的状态v,f[i][j]=(f[i-1][j^v]+f[i-1][j])*(1<<(sum-1)) 因为空间太多了,需要用滚动数组 int pri[]={0,2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67}; int n; int f[2][1<<20],sum[80],p[100010],mod=1e9+7; int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) sum[read()]++; p[0]=1; for(int i=1;i<=n;i++) p[i]=p[i-1]*2%mod; f[0][0]=1; for(int i=1;i<=70;i++) { if(sum[i]==0) { for(int k=0;k<(1<<20);k++) f[i&1][k]=f[(i-1)&1][k]; continue; } int v=0,ttt=i; for(int j=1;j<=19;j++) while(ttt%pri[j]==0) { ttt=ttt/pri[j]; v=v^(1<<j); } for(int k=0;k<(1<<20);k++) f[i&1][k]=1ll*(f[(i-1)&1][k^v]+f[(i-1)&1][k])*p[sum[i]-1]%mod; } cout<<(f[0][0]-1+mod)%mod; }

考虑枚举每一对劫匪和灯 如果a[i]>c[j]||b[i]>d[j]当然不影响 否则,这一对灯传递给我们一个信息:当x方向移动小于等于cj-ai时,y方向至少要移动d[j]-b[i]+1 把这些规定用区间修改搞一搞,最后枚举x方向移动大小,计算至少y方向要移动多少,计算答案 因为先修改,最后计算答案,所以可以倒着更新一下 int n,m,a[2010],b[2010],c[2010],d[2010]; int f[1000010],ans; int main() { // freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++) a[i]=read(),b[i]=read(); for(int i=1;i<=m;i++) c[i]=read(),d[i]=read(); for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { if(a[i]>c[j]||b[i]>d[j])continue; f[c[j]-a[i]]=max(f[c[j]-a[i]],d[j]-b[i]+1); } } ans=3e6; for(int i=1000000;i>=0;i--) { f[i]=max(f[i],f[i+1]); ans=min(ans,f[i]+i); } cout<<ans; }

首先注意到,如果两个机器人刚开始时,所处位置奇偶不同,那么他们一辈子也遇不到 所以一个性质是只有初始位置在奇数的才能和奇数的碰撞,偶数的才能和偶数的碰撞,最多有两个-1 然后考虑从左到右地看每个机器人 如果上一个没死的机器人是向左的或者向右的,我也是向左的,那么一定我俩撞上 如果我是向右的,那么就说不定了,所以扔到堆里 这样操作一遍下来,可以发现栈里还剩一堆右,最多就是最开始会有一个左 如果剩下来的是奇数个,那么第一个一定-1,其他的互相撞。否则大家互相撞,两个两个匹配 是一个乱搞的题 vector<int>q[2]; int n,m,ans[300010]; struct node { int x,i; char c; friend bool operator <(node a,node b) { return a.x<b.x; } }o[300010]; void work() { n=read();m=read(); for(int i=1;i<=n;i++) { o[i].x=read(); o[i].i=i; } q[0].clear();q[1].clear(); for(int i=1;i<=n;i++) cin>>o[i].c; sort(o+1,o+1+n); for(int i=1;i<=n;i++) { int t=o[i].x&1; if(q[t].empty()) q[t].push_back(i); else { int pre=q[t].back(); if(o[pre].c=='L'&&o[i].c=='L') { ans[o[i].i]=ans[o[pre].i]=(o[i].x-o[pre].x)/2+o[pre].x; q[t].pop_back(); } else if(o[pre].c=='R'&&o[i].c=='R') q[t].push_back(i); else if(o[pre].c=='L'&&o[i].c=='R') q[t].push_back(i); else if(o[pre].c=='R'&&o[i].c=='L') { ans[o[i].i]=ans[o[pre].i]=(o[i].x-o[pre].x)/2; q[t].pop_back(); } } } for(int t=0;t<2;t++) { for(int j=q[t].size()-1;j-1>=0;j-=2) { int i=q[t][j],pre=q[t][j-1]; if(o[pre].c=='R'&&o[i].c=='R') ans[o[i].i]=ans[o[pre].i]=(o[i].x-o[pre].x)/2+m-o[i].x; else if(o[pre].c=='L'&&o[i].c=='R') ans[o[i].i]=ans[o[pre].i]=(2*m-o[i].x+o[pre].x)/2; } if(q[t].size()&1) ans[o[q[t][0]].i]=-1; } for(int i=1;i<=n;i++) printf("%d ",ans[i]); printf("\n"); } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

经典最小最短路树 考虑跑一跑经典最短路,记录每个点是谁更新的。这还不够,如果pre有更优的选择,就需要更新pre int n,m,tot,head[300010],v[300010],fa[300010]; struct edge { int x,y,v,i,next; friend bool operator <(edge a,edge b) { return a.v<b.v; } }e[600010]; void add(int x,int y,int v,int i) { tot++; e[tot]={x,y,v,i,head[x]}; head[x]=tot; } int get(int x) { return fa[x]==x?x:fa[x]=get(fa[x]); } ll d[300010],sum,pre[300010],u; priority_queue<pair<ll,int>>q; priority_queue<int>ans; int main() { // freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++) fa[i]=i; for(int i=1;i<=m;i++) { int x=read(),y=read(),v=read(); add(x,y,v,i); add(y,x,v,i); } memset(d,0x3f,sizeof(d)); u=read(); d[u]=0; q.push({0,u}); while(q.size()) { int x=q.top().second; q.pop(); if(v[x])continue; v[x]=1; for(int i=head[x];i;i=e[i].next) { int y=e[i].y; if(d[y]>d[x]+e[i].v) { d[y]=d[x]+e[i].v; q.push({-d[y],y}); pre[y]=i; } else if(d[y]==d[x]+e[i].v&&e[pre[y]].v>e[i].v) pre[y]=i; } } for(int i=1;i<=n;i++){ if(i==u)continue; sum=sum+e[pre[i]].v; ans.push(-e[pre[i]].i); } printf("%lld\n",sum); while(ans.size()) { printf("%d ",-ans.top()); ans.pop(); } }

先把块内排个序 答案是n-最长子序列长度 int k1,k2,k3,n; int a[200010]; vector<int>o; int main() { // freopen("1.in","r",stdin); k1=read();k2=read();k3=read(); n=k1+k2+k3; for(int i=1;i<=n;i++) a[i]=read(); sort(a+1,a+1+k1); sort(a+k1+1,a+1+k1+k2); sort(a+k1+k2+1,a+1+n); for(int i=1;i<=n;i++) { if(o.empty()||a[i]>o.back()) o.push_back(a[i]); else o[lower_bound(o.begin(),o.end(),a[i])-o.begin()]=a[i]; } cout<<n-o.size(); }

考虑假如知道了a[1]的值 那么询问n-1次a[1]^a[i]就可以得知全部ai的值 感觉有点接近,那么先询问一下 然后注意到值域大小=n 1、如果存在两个数字相等,也就是a[1]^a[x]=a[1]^a[y] 那么询问一下a[x]&a[y]就可以得知a[x] 进而得到a[1] 2、如果全都不等,那么a[1]^a[i]一定是[1,n-1] 这个时候考虑把a[1]^a[x]=2和a[1]^a[y]=3的下标拿出来, a[x]&a[y]和a[i]的关系是:前k-2位都相同,倒数第二位取反,倒数第一位没啥关系 就剩一位了,那好说,考虑问一下a[1]&a[x],他俩的最后一位是相同的 综上,可以用最多n+1次得到ai int n,a[70000]; int v[70000]; void print() { for(int i=2;i<=n;i++) a[i]=a[i]^a[1]; cout<<"!"; for(int i=1;i<=n;i++) cout<<' '<<a[i]; cout<<endl; exit(0); } int main() { n=read(); for(int i=2;i<=n;i++) { cout<<"XOR 1 "<<i<<endl; a[i]=read(); } for(int i=1;i<=n;i++) { if(v[a[i]]) { cout<<"AND "<<i<<' '<<v[a[i]]<<endl; a[1]=a[i]^read(); print(); } v[a[i]]=i; } cout<<"AND "<<v[2]<<' '<<v[3]<<endl; a[1]=((read()/2)^1)*2; cout<<"AND "<<1<<' '<<v[2]<<endl; a[1]=a[1]+(read()&1); print(); }

考虑三分 问题转化成已知x,求序列bi=ai-x的最大{子段和的绝对值} 可以跑两遍,第一遍求最大子段和,第二遍求最小子段和 int n; double l,r,lmid,rmid,b[200010],a[200010]; double ask(double x) { double t=0,sum=0; for(int i=1;i<=n;i++) b[i]=a[i]-x; for(int i=1;i<=n;i++) { if(sum<0) sum=b[i]; else sum=sum+b[i]; t=max(sum,t); } sum=0; for(int i=1;i<=n;i++) { if(sum>0) sum=b[i]; else sum=sum+b[i]; t=max(-sum,t); } return t; } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) a[i]=read(),r=max(r,fabs(a[i])); l=-r; for(int i=1;i<=100;i++) { lmid=l+(r-l)/3; rmid=r-(r-l)/3; if(ask(lmid)>=ask(rmid)) l=lmid; else r=rmid; } printf("%.8lf",ask(l)); }

也太简单了。。 f[i][j][k]表示在i*j的矩形里得到k个的最小花费 然后枚举划的最后一刀,枚举在一边获得kk个,另一边获得k-kk个,进行转移 复杂度30*30*50*50*30 int f[40][40][60]; int main() { // freopen("1.in","r",stdin); memset(f,0x3f,sizeof(f)); for(int i=1;i<=30;i++) for(int j=1;j<=30;j++) { if(i*j<=50) f[i][j][i*j]=0; f[i][j][0]=0; for(int k=1;k<=min(i*j,50);k++) for(int kk=0;kk<=k;kk++) { for(int ii=1;ii<i;ii++) f[i][j][k]=min(f[ii][j][kk]+f[i-ii][j][k-kk]+j*j,f[i][j][k]); for(int jj=1;jj<j;jj++) f[i][j][k]=min(f[i][jj][kk]+f[i][j-jj][k-kk]+i*i,f[i][j][k]); } } for(int t=read();t;t--) { int n=read(),m=read(),k=read(); printf("%d\n",f[n][m][k]); } }

首先注意到假如有m种不同数字,那么答案最大是m 如果数字x要提到前面,那么所有小于x的数字也要被提一次(在他之后 如果x要提到后面,那么所有大于x的数字也要被提一次 考虑枚举往前提l个 到这里我发现好像需要离散化,所以搞一搞 那么如果要往前提1到l 那么考虑除了这些数字,剩下来的数字至少要提到几 考虑剩下的数字,如果存在逆序对a[i]>a[j]且i<j,就要提ai与大于他的数字 所以预处理一个maxmin[x]数组表示在x后面的,比x小的数字的最大值,这一块可以用线段树。他表示这,当且仅当,至少已经往前提了1到maxmin[x]后,就不需要往后提x了 那么就可以开始双指针了。枚举要往前提1到l,往后提r到m+1 每次l++,r有可能可以增大 更新答案 int n,m,a[300010],b[300010],maxx[1200010],lazy[1200010],maxmin[300010]; vector<int>pos[300010]; void pushdown(int x) { maxx[x*2]=max(maxx[x*2],lazy[x]); maxx[x*2+1]=max(maxx[x*2+1],lazy[x]); lazy[x*2]=max(lazy[x],lazy[x*2]); lazy[x*2+1]=max(lazy[x],lazy[x*2+1]); } int askmax(int x,int l,int r,int pos)//pos,n { if(pos<=l) return maxx[x]; int mid=(l+r)/2; pushdown(x); if(pos<=mid) return max(maxx[x*2+1],askmax(x*2,l,mid,pos)); return askmax(x*2+1,mid+1,r,pos); } void add(int x,int l,int r,int pos,int v)//1,pos { maxx[x]=v; if(pos>=r) { lazy[x]=v; return ; } int mid=(l+r)/2; pushdown(x); if(pos>mid) add(x*2+1,mid+1,r,pos,v); add(x*2,l,mid,pos,v); } void work() { n=read(); for(int i=1;i<=4*n;i++) maxx[i]=lazy[i]=0; for(int i=1;i<=n;i++) b[i]=a[i]=read(); sort(b+1,b+1+n); m=unique(b+1,b+1+n)-b-1; for(int i=1;i<=m;i++) pos[i].clear(); for(int i=1;i<=n;i++) { a[i]=lower_bound(b+1,b+1+m,a[i])-b; pos[a[i]].push_back(i); } for(int i=1;i<=m;i++) { maxmin[i]=0; for(auto j:pos[i]) maxmin[i]=max(maxmin[i],askmax(1,1,n,j)); for(auto j:pos[i]) add(1,1,n,j,i); } int l=0,r=m+1,ans=m; for(int i=1;i<=m;i++) if(maxmin[i]!=0) { r=i; break; } for(;l<=m;l++) { while(r<=m&&maxmin[r]<=l) r++; ans=min(ans,l+m-r+1); } printf("%d\n",ans); } int main() { // freopen("1.in","r",stdin); for(int q=read();q;q--) work(); }

如果n<=4,那么一定有解 否则考虑1 2 3 这仨点,要么共线,要么是三角形也就是一条直线过两个点,另一条直线过另外一个点。所以考虑枚举这个锅两个点的直线过的是哪两个点,只有1 2 ,2 3 ,1 3 这三种情况 work函数内部,如果这个点和X1X2共线就continue 否则如果X3和X4还没确定下来,就占据一个位子 如果X3X4已经确定下来了,就必须和X3X4共线 如果确定下来但是一个也不共线的话就可以return了 int n; ll x[100010],y[100010]; void work(int X1,int X2) { int X3=0,X4=0; for(int i=1;i<=n;i++) { if(i==X1||i==X2) continue; if(X3&&X4) { if((y[i]-y[X2])*(x[X2]-x[X1])!=(y[X2]-y[X1])*(x[i]-x[X2])&&(y[i]-y[X4])*(x[X4]-x[X3])!=(y[X4]-y[X3])*(x[i]-x[X4])) return ; } else if((y[i]-y[X2])*(x[X2]-x[X1])!=(y[X2]-y[X1])*(x[i]-x[X2])) { if(X3) X4=i; else X3=i; } } printf("YES"); exit(0); } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) x[i]=read(),y[i]=read(); work(1,2); work(2,3); work(1,3); printf("NO"); }

写了半天dp,然后感觉好难写,因为最后要还原现场 那么考虑大胆贪心 注意到%3==0的数字删不删都不影响和%3,那么关键就在于%3=1和%3=2了 如果1的数量大于等于3且2的数量大于等于3,那么可以贪心地删最后几个1或者最后几个2使得%3==0 如果都小于3的话,比如现在%3==1 那么要么1的数量是1,要么2的数量是2,贪心地删了他们即可 想是这么想,写代码的时候可以if2的数量小于2,那么一定1个1导致了%3=1,if 1的数量小于1,那么一定2个2导致了%3=1,如果都挺多的,那可以删最后俩2或者删最后一个1 本来写了个work函数返回一个string的,但是会超时。就把vector改成了数组,子函数写成了两个,一个是询问长度的,一个是确定了答案后输出的 char s[100010]; int n,flag[100010],len[4]; int pos[4][100010]; void print(int x,int y) { for(int i=1;i<=n;i++) flag[i]=1;//可以保留 for(int i=len[1];i>len[1]-x;i--) flag[pos[1][i]]=0; for(int i=len[2];i>len[2]-y;i--) flag[pos[2][i]]=0; int l=1; while(l<=n&&(flag[l]==0||s[l]=='0')) l++; if(l==n+1) { if(len[0]) cout<<"0"; else cout<<"-1"; } else for(;l<=n;l++) if(flag[l]) cout<<s[l]; } int work(int x,int y)//删去最后x个1,y个2 { string t=""; int sum=0; for(int i=1;i<=n;i++) flag[i]=1;//可以保留 for(int i=len[1];i>len[1]-x;i--) flag[pos[1][i]]=0; for(int i=len[2];i>len[2]-y;i--) flag[pos[2][i]]=0; int l=1; while(l<=n&&(flag[l]==0||s[l]=='0')) l++; if(l==n+1) { if(len[0]) return 1; } else for(;l<=n;l++) sum+=flag[l]; return sum; } int main() { // freopen("1.in","r",stdin); std::ios::sync_with_stdio(0); cin.tie(NULL); cout.tie(NULL); cin>>(s+1); n=strlen(s+1); for(int i=1;i<=n;i++) { int x=(s[i]-'0')%3; len[x]++; pos[x][len[x]]=i; } if((len[1]+len[2]*2)%3==0) cout<<(s+1); else if((len[1]+len[2]*2)%3==2) { if(len[1]<2) print(0,1); else if(len[2]<1) print(2,0); else { if(work(0,1)>work(2,0)) print(0,1); else print(2,0); } } else if((len[1]+len[2]*2)%3==1) { if(len[2]<2) print(1,0); else if(len[1]<1) print(0,2); else { if(work(0,2)>work(1,0)) print(0,2); else print(1,0); } } }

就试了试没想到过了 考虑贪心地每次从叶子节点拿出来芽,然后重构树,把芽拼起来 那么每次拼会多sum个叶子少一个叶子 dfs搜一下即可 flag[x]=1表示我交给我父亲带走,=0表示我作为芽带走还没走的儿子 int ans,n,flag[200010]; vector<int>e[200010]; void dfs(int x,int fa) { int sumboy=0; for(auto y:e[x]) { if(y==fa)continue; dfs(y,x); if(flag[y]) sumboy++; } if(sumboy==0) flag[x]=1; else { flag[x]=0; ans=ans+sumboy-1; } } void work() { n=read();ans=0; for(int i=1;i<=n;i++) e[i].clear(); for(int i=1;i<n;i++) { int x=read(),y=read(); e[x].push_back(y); e[y].push_back(x); } dfs(1,0); cout<<ans+1<<endl; } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

考虑如果众数出现了x次,一定可以把区间划分为2*x-len个合法 如果没有众数那就是1 所以考虑线段树求众数,在合并时再用一个log求数字在区间里出现的次数即可。 复杂度(n+q)log^2n vector<int>pos[300010]; int a[300010],v[1200010],n,q; int ask(int v1,int v2,int l,int r) { int sum1=upper_bound(pos[v1].begin(),pos[v1].end(),r)-lower_bound(pos[v1].begin(),pos[v1].end(),l); int sum2=upper_bound(pos[v2].begin(),pos[v2].end(),r)-lower_bound(pos[v2].begin(),pos[v2].end(),l); if(sum1>sum2) return v1; return v2; } int asksum(int v,int l,int r) { return upper_bound(pos[v].begin(),pos[v].end(),r)-lower_bound(pos[v].begin(),pos[v].end(),l); } void build(int x,int l,int r) { if(l==r) { v[x]=a[l]; return ; } int mid=(l+r)/2; build(x*2,l,mid); build(x*2+1,mid+1,r); v[x]=ask(v[x*2],v[x*2+1],l,r); } int work(int x,int l,int r,int tl,int tr) { if(tl<=l&&r<=tr) return v[x]; int mid=(l+r)/2; if(tr<=mid) return work(x*2,l,mid,tl,tr); else if(mid<tl) return work(x*2+1,mid+1,r,tl,tr); else return ask(work(x*2,l,mid,tl,tr),work(x*2+1,mid+1,r,tl,tr),tl,tr); } int main() { // freopen("1.in","r",stdin); n=read();q=read(); for(int i=1;i<=n;i++) { a[i]=read(); pos[a[i]].push_back(i); } build(1,1,n); for(;q;q--) { int tl=read(),tr=read(); printf("%d\n",max(1,asksum(work(1,1,n,tl,tr),tl,tr)*2-(tr-tl+1))); } }

考虑枚举左端点,右端点向右移动时,gcd单调不增,而减小的次数最多为log(a[i])次。所以考虑暴力地枚举左端点,把所有可能的gcd都求出来并丢给map 然后输出 用st表复杂度为O(nlog^3(n)),一个log是减小的次数,一个log是二分,一个log是__gcd的。不过实际跑起来却挺快。(可能我算错了?) int st[100010][20],n,a[100010]; map<int,ll>o; int ask(int l,int r) { int k = log2(r-l+1); return __gcd(st[l][k],st[r-(1<<k)+1][k]); } int work(int lpos,int rpos) { int val=ask(lpos,rpos); if(ask(lpos,n)==val)//等于val的最后一个 return n; int l=rpos,r=n,mid; while(l+1<r) { mid=(l+r)/2; if(ask(lpos,mid)==val) l=mid; else r=mid; } if(ask(lpos,r)==val) return r; return l; } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) a[i]=read(); for(int i=1;i<=n;i++) st[i][0]=a[i]; for(int i=1;i<=20;i++) { int len=1<<(i-1); for(int j=1;j+(1<<i)-1<=n;j++) st[j][i]=__gcd(st[j][i-1],st[j+len][i-1]); } for(int i=1;i<=n;i++) { int r1=i,r2=work(i,i); while(1) { o[ask(i,r1)]+=r2-r1+1; r1=r2+1; if(r1<=n) r2=work(i,r1); else break; } } for(int i=read();i;i--) printf("%lld\n",o[read()]); }

为什么这么水的背包也能2000分 考虑开一个100*2000的背包计算最大值 对于每个状态f[i][j],记录g[i][j]若为1则表示我是通过选i号物品得到的f[i][j]=f[i-1][j-o[i].t]+o[i].p,否则是不选i好物品得到的f[i][j]=f[i-1][j]。找到最大值后回溯即可。 int n,f[110][2010],g[110][2010]; struct node { int t,d,p,i; friend bool operator <(node a,node b) { return a.d<b.d; } }o[110]; stack<int>ans; void work(int x,int sum) { if(x==0) return ; if(g[x][sum]) { ans.push(o[x].i); work(x-1,sum-o[x].t); } else work(x-1,sum); } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) { o[i].t=read();o[i].d=read(); o[i].p=read();o[i].i=i; } sort(o+1,o+1+n); for(int i=1;i<=n;i++) { for(int j=0;j<o[i].t;j++) f[i][j]=f[i-1][j]; for(int j=o[i].t;j<=2000;j++) { if(o[i].d>j&&f[i-1][j]<f[i-1][j-o[i].t]+o[i].p) { f[i][j]=f[i-1][j-o[i].t]+o[i].p; g[i][j]=1; } else f[i][j]=f[i-1][j]; } } int t=0; for(int i=1;i<=2000;i++) if(f[n][i]>f[n][t]) t=i; printf("%d\n",f[n][t]); work(n,t); printf("%d\n",ans.size()); while(ans.size()) { printf("%d ",ans.top()); ans.pop(); } }

考虑首先跑一个dfs序,记录pos[i]表示i的dfs序,lp[i]和rp[i]为i的子树的dfs序的区间。 那么子树翻转和子树亮灯的点的数量可以使用线段树完成,子树翻转变为区间翻转,打懒标记即可。子树亮灯的点的数量为区间求和。 int tot,n,lp[200010],rp[200010],b[200010][2],lazy[800010],sum[800010][2]; int pos[200010]; vector<int>e[200010]; char s[10]; void add(int x,int l,int r,int v0,int v1,int d) { sum[x][0]+=v0; sum[x][1]+=v1; if(l==r) { return ; } int mid=(l+r)/2; if(d<=mid) add(x*2,l,mid,v0,v1,d); else add(x*2+1,mid+1,r,v0,v1,d); } void dfs(int x) { tot++; lp[x]=pos[x]=tot; for(auto y:e[x]) dfs(y); rp[x]=tot; } void pushdown(int x) { if(!lazy[x])return ; lazy[x]=0; lazy[x*2]^=1; lazy[x*2+1]^=1; swap(sum[x*2][0],sum[x*2][1]); swap(sum[x*2+1][0],sum[x*2+1][1]); } int ask(int x,int l,int r,int tl,int tr) { if(tl<=l&&r<=tr) return sum[x][1]; int mid=(l+r)/2; pushdown(x); int tsum=0; if(tl<=mid) tsum+=ask(x*2,l,mid,tl,tr); if(tr>mid) tsum+=ask(x*2+1,mid+1,r,tl,tr); return tsum; } void swapp(int x,int l,int r,int tl,int tr) { if(tl<=l&&r<=tr){ lazy[x]^=1; swap(sum[x][0],sum[x][1]); return ; } pushdown(x); int mid=(l+r)/2; if(tl<=mid) swapp(x*2,l,mid,tl,tr); if(tr>mid) swapp(x*2+1,mid+1,r,tl,tr); sum[x][0]=sum[x*2][0]+sum[x*2+1][0]; sum[x][1]=sum[x*2][1]+sum[x*2+1][1]; } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=2;i<=n;i++) e[read()].push_back(i); dfs(1); for(int i=1;i<=n;i++) if(read()&1) add(1,1,n,0,1,pos[i]); else add(1,1,n,1,0,pos[i]); for(int q=read();q;q--) { int x; scanf("%s%d",s,&x); if(s[0]=='g') printf("%d\n",ask(1,1,n,lp[x],rp[x])); else swapp(1,1,n,lp[x],rp[x]); } }

考虑乱搞 因为答案串最多26个字母,所以枚举这o.size()位,寻找最大的可用的字母,找到后令en[]=-1表示已经被用过了。同时注意如果s[j]==en[s[j]]证明该字母为最后一个了,不能被跳过去,所以要break char s[200010]; int n,m,en[300]; map<int,int>o; void work() { scanf("%s",s); n=strlen(s); o.clear(); for(int i='a';i<='z';i++) en[i]=0; for(int i=0;i<n;i++) { o[s[i]]=1; en[s[i]]=i; } m=o.size(); int now=0; for(int i=1;i<=m;i++) { char maxx=0; for(int j=now;j<n;j++) { if(en[s[j]]==-1)//已经被用过了 continue; if(s[j]>maxx) { now=j; maxx=s[j]; } if(j==en[s[j]])//是最后一个,无法删除 break; } printf("%c",maxx); en[maxx]=-1; } printf("\n"); } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

注意到a string of moves s of length at most 4,而如果为3或4的话不容易控制,可以猜到他是为了一拐一拐地前进。 然后开始构造,斜着一列一列地过去再回来,发现有三种情况并且需要预先跑一半边界跑到对角,从对角开始运行。 构造一下后发现恰好需要大概3000步,所以应该就是正解了。 然后先实现一下全都跑一遍的,再实现只要前k步的。 草,看了一下题解发现题解简单的多的多得多 唉,自闭了 int n,m,k; queue<pair<string,int>>q; void add(string s,int x) { if(s.length()*x<k) { q.push({s,x}); k=k-s.length()*x; return ; } if(s.length()==1) q.push({s,k}); else { if(k!=1) q.push({s,k/2}); if(k&1) { s=s.substr(0,1); q.push({s,1}); } } printf("%d\n",q.size()); while(q.size()) { cout<<q.front().second<<' '<<q.front().first<<endl; q.pop(); } exit(0); } int main() { n=read();m=read();k=read(); if(4*n*m-2*n-2*m<k) { printf("NO"); return 0; } printf("YES\n"); if(m!=1) add("R",m-1); if(n!=1) add("D",n-1); for(int i=1;i<=min(n,m)-1;i++) { add("L",1); if(i!=1) add("DL",i-1); add("RU",i); } for(int i=1;i<=max(n,m)-min(n,m);i++) { if(min(n,m)!=1) add("LD",min(n,m)-1); if(n<m) add("L",1); else add("U",1); if(min(n,m)!=1) add("RU",min(n,m)-1); } for(int j=min(n,m)-1;j;j--) { add("LD",j); add("U",1); if(j!=1) add("RU",j-1); } }

之前写的,忘了 struct node { ll v,x,y; friend bool operator <(node a,node b) { return a.v<b.v; } }; priority_queue<node>q; ll a[200010][3],n,ans,now; void work() { n=read(); for(int i=1;i<=2;i++) for(int j=1;j<=n;j++) a[j][i]=read(); for(int i=1;i<=n;i++) { q.push({a[i][1]+2*n-i+1,i,1}); q.push({a[i][2]+i,i,2}); } if(q.top().x==1&&q.top().y==1) q.pop(); now=0; ans=q.top().v; for(int i=1;i<=n;i+=2) { while(q.size()&&q.top().x<i) q.pop(); ans=min(ans,max(now+2*(n-i+1),q.top().v-i+1)); if(i!=1) now=max(now,a[i][1])+1; now=max(now,a[i][2])+1; now=max(now,a[i+1][2])+1; now=max(now,a[i+1][1])+1; } while(q.size())q.pop(); for(int i=1;i<=n;i++) { q.push({a[i][2]+2*n-i+1,i,2}); q.push({a[i][1]+i,i,1}); } now=0; now=max(now,a[1][2])+1; for(int i=2;i<=n;i+=2) { while(q.size()&&q.top().x<i)q.pop(); ans=min(ans,max(now+2*(n-i+1),q.top().v-i+1)); now=max(now,a[i][2])+1; now=max(now,a[i][1])+1; now=max(now,a[i+1][1])+1; now=max(now,a[i+1][2])+1; } while(q.size())q.pop(); printf("%lld\n",ans); } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

简单dfs 首要条件是sum%3==0 然后考虑如何找到分割点 维护一个当前子树和t[x],答案要么是t[x]=sum/3,t[y]=sum/3,x和y不是祖先关系。要么t[x]=sum/3,t[y]=sum/3*2,y是x的祖先,并且y不是根。用dfs维护一下即可 int n,sum,t[1000010]; vector<int>e[1000010]; int dfs(int x) { int flag=0,tt; for(auto y:e[x]) { tt=dfs(y); t[x]+=t[y]; if(tt&&flag) { printf("%d %d",tt,flag); exit(0); } if(tt) flag=tt; } if(flag&&t[x]==sum*2&&x!=e[0][0]) { printf("%d %d",flag,x); exit(0); } if(t[x]==sum) return x; if(flag) return flag; return 0; } int main() { n=read(); for(int i=1;i<=n;i++) { e[read()].push_back(i); t[i]=read(); sum=sum+t[i]; } if(sum%3==0) { sum=sum/3; dfs(e[0][0]); } printf("-1"); }

大胆暴力 考虑答案要么是原串前后加1,要么是翻转前后加一,要么是删掉后缀0前后加一,要么是删掉后缀0前后加一,枚举一下然后判断暴力判断。注意细节 ll x,y; string s,s1,t; int fl[1000],fr[1000]; int main() { // freopen("1.in","r",stdin); x=read(); y=read(); while(x) { s=char('0'+(x&1))+s; x=x/2; } s1=s; while(s1[s1.length()-1]=='0') s1=s1.erase(s1.length()-1,1); while(y) { t=char('0'+(y&1))+t; y=y/2; } if(s==t) { printf("YES"); return 0; } for(int i=0;i<t.length();i++) { if(t[i]=='0') break; fl[i]=1; } fr[t.length()]=1; for(int i=t.length()-1;i>=0;i--) { if(t[i]=='0') break; fr[i]=1; } for(int l=0,r=s.length()-1;r<t.length();l++,r++) { if(s==t.substr(l,s.length())&&(l==0||fl[l-1])&&fr[r+1]) { if(r!=t.length()-1||s[s.length()-1]=='1') { cout<<"YES"; return 0; } } } for(int l=0,r=s1.length()-1;r<t.length();l++,r++) { if(s1==t.substr(l,s1.length())&&(l==0||fl[l-1])&&fr[r+1]) { cout<<"YES"; return 0; } } reverse(s1.begin(),s1.end()); for(int l=0,r=s1.length()-1;r<t.length();l++,r++) { if(s1==t.substr(l,s1.length())&&(l==0||fl[l-1])&&fr[r+1]) { cout<<"YES"; return 0; } } reverse(s.begin(),s.end()); for(int l=0,r=s.length()-1;r<t.length();l++,r++) { if(s==t.substr(l,s.length())&&(s[0]!='0'&&l==0||fl[l-1])&&fr[r+1]) { cout<<"YES"; return 0; } } cout<<"NO"; }

又是经典的dp然后逆着跑一遍输出方案的题 首先考虑应该把ai排序后进行配队,然后每个队最多选五个人,但凡有六个人以上一定可以拆成两个队伍使得答案更小。 答案并不是贪心,选n/3个队伍,而是进行dp。我写的是f[i][j]表示当i为队伍里的第j个人时的最小代价之和。j取1到5。实际上是在对于b[i]=ai-a[i-1]数组选若干个数删掉,使得总和最小。 输出方案时是普通的循环或者dfs跑一跑。 int n,cnt; ll f[200010][10]; struct node { int v,i,ans; }o[200010]; bool v_(node a,node b) { return a.v<b.v; } bool i_(node a,node b) { return a.i<b.i; } void work(int x,int now) { if(x==0)return ; o[x].ans=cnt; if(now==1) { cnt++; if(f[x][1]==f[x-1][3]) work(x-1,3); else if(f[x][1]==f[x-1][4]) work(x-1,4); else work(x-1,5); } else work(x-1,now-1); } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) { o[i].v=read(); o[i].i=i; } sort(o+1,o+1+n,v_); memset(f,0x3f,sizeof(f)); f[1][1]=0; for(int i=2;i<=n;i++) { f[i][1]=min(f[i-1][3],min(f[i-1][4],f[i-1][5])); for(int j=2;j<=5;j++) f[i][j]=f[i-1][j-1]+o[i].v-o[i-1].v; } cnt++; if(f[n][3]<=f[n][4]&&f[n][3]<=f[n][5]) work(n,3); else if(f[n][4]<=f[n][3]&&f[n][4]<=f[n][5]) work(n,4); else work(n,5); printf("%lld %d\n",min(f[n][3],min(f[n][4],f[n][5])),cnt-1); sort(o+1,o+1+n,i_); for(int i=1;i<=n;i++) printf("%d ",o[i].ans); }

考虑线段树维护区间最值,将蛋糕记录下标i并按体积排序后,每次使用线段树求区间最大值并更新。 int n; ll maxx[400010]; struct node { ll v,ans; int i; friend bool operator <(node a,node b) { return a.v<b.v; } }o[100010]; ll ask(int x,int l,int r,int d) { if(r<=d) return maxx[x]; int mid=(l+r)/2; if(d<=mid) return ask(x*2,l,mid,d); else return max(maxx[x*2],ask(x*2+1,mid+1,r,d)); } void add(int x,int l,int r,int d,ll v) { maxx[x]=max(maxx[x],v); if(l==r) return ; int mid=(l+r)/2; if(d<=mid) add(x*2,l,mid,d,v); else add(x*2+1,mid+1,r,d,v); } int main() { // freopen("1.in","r",stdin); n=read(); ll tr,th; for(int i=1;i<=n;i++) { tr=read();th=read(); o[i].v=tr*tr*th; o[i].i=i; } sort(o+1,o+1+n); for(int i=1;i<=n;) { int l=i,r=i; while(o[r+1].v==o[i].v) r++; for(int j=l;j<=r;j++) o[j].ans=ask(1,1,n,o[j].i)+o[j].v; for(int j=l;j<=r;j++) add(1,1,n,o[j].i,o[j].ans); i=r+1; } printf("%.8lf",acos(-1)*maxx[1]); }

考虑记录一下全体最小值minn,最大值maxx 若maxx<=minn*2,则全输出-1 否则对于每个位置,最多听n-1首也就结束了 考虑对于每个位置,如果是>minn*2的,就去找最少听几首,最小值可以使自己停下来,记录一下 例如第三个位置听三个就可以停下来,那么第二个位置最多听四个可以停下来,第一个位置最多五个,第n个最多六个,以此类推。当然,可能更小 所以用p[i]给全体更新答案,为了让大家都跑n次,应该至少跑2*n次,更新答案。 int f[200010][20],n,a[200010],p[200010],ans[100010]; int askmin(int l,int r) { int k=log2(r-l+1); return min(f[l][k],f[r-(1<<k)+1][k]); } int ask(int x) { int l=x+1,r=x+n,mid; while(l+1<r) { mid=(l+r)/2; if(a[x]>askmin(x,mid)*2) r=mid; else l=mid; } if(a[x]>askmin(x,l)*2) return l-x; else return r-x; } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) a[i+n]=a[i]=read(); int minn,maxx; minn=maxx=a[1]; for(int i=1;i<=n;i++) { minn=min(minn,a[i]); maxx=max(maxx,a[i]); } if(maxx<=minn*2) { for(int i=1;i<=n;i++) printf("-1 "); return 0; } for(int i=1;i<=2*n;i++) f[i][0]=a[i]; for(int j=1;j<20;j++) for(int i=1;i+(1<<(j-1))<=2*n;i++) f[i][j]=min(f[i][j-1],f[i+(1<<(j-1))][j-1]); memset(ans,0x3f,sizeof(ans)); for(int i=1;i<=n;i++) if(a[i]>minn*2) p[i]=ask(i); else p[i]=2*n; int now=10*n; for(int i=n,j=0;j<=3*n;i=(i+n-2)%n+1,j++) { now=min(now+1,p[i]); ans[i]=min(ans[i],now); } for(int i=1;i<=n;i++) printf("%d ",ans[i]); }

考虑dp f[i][j]表示位置使用的状态为i,%m=j的方案数 对于每个数字,暴力地枚举状态,从1的数量等于now的状态推到1的数量等于now+1的状态 枚举数字再枚举状态复杂度为len*(1<<len),每个状态往外递推len次,总的复杂度为O(len*(1<<len)) ll f[500000][110],sum[20],jie[20]; ll n,m,len,now,po[20],ask[500000]; void add(ll x) { for(int i=0;i<(1<<len);i++) if(ask[i]==now) for(int j=0;j<len;j++) if((i&(1ll<<j))==0) for(int k=0;k<m;k++) f[i+(1<<j)][(k+x*po[j])%m]+=f[i][k]; now++; } int main() { // freopen("1.in","r",stdin); n=read();m=read(); while(n) { sum[n%10]++; len++; n=n/10; } jie[0]=po[0]=1; for(int i=1;i<=18;i++) jie[i]=jie[i-1]*i,po[i]=po[i-1]*10; for(int i=0;i<(1<<len);i++) ask[i]=ask[i/2]+(i&1); now=sum[0]; for(int i=0;i<(1<<len);i++) if((i&(1<<(len-1)))==0 &&ask[i]==sum[0]) f[i][0]=1;//位置状态为i,%m=0 的方案数 for(int i=1;i<=9;i++) { for(int j=1;j<=sum[i];j++) add(i); for(int j=0;j<(1<<len);j++) { if(ask[j]==now) for(int k=0;k<m;k++) f[j][k]/=jie[sum[i]]; } } printf("%lld",f[(1<<len)-1][0]); }
完结撒花✿✿ヽ(°▽°)ノ✿。
虽然好像题解没够100,但是确实第一页刷完了。











【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】