树的dfs序,p1539,p1651,,2018/11/08模拟赛T3
树的欧拉序指从根节点进行dfs(先序遍历),每次到达某个点的时间和离开这个点的时间.它可以将树上的问题转换成序列问题进行处理.
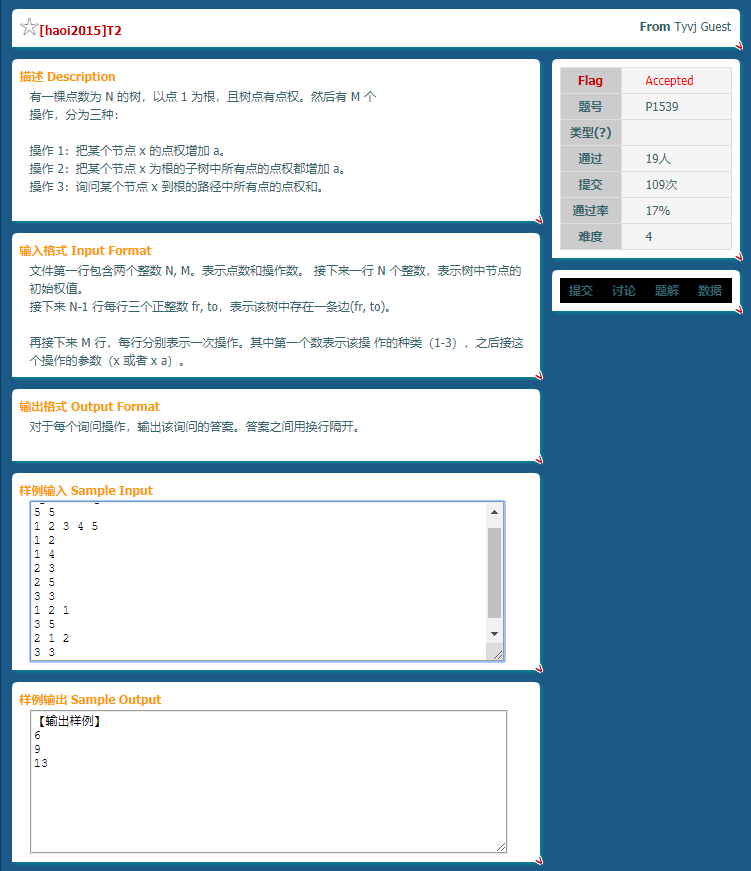
比如对于p1539的样例可以这样解释.
每个点的左边数字表示进入该点的"时间",右边的数字表示离开该点的"时间".对欧拉序的介绍就到这里.
然后来看一个例题:
先读入边,跑一遍dfs确定欧拉序.
对于操作1,把点x的进入的"时间"+=a,把x出去的"时间"-=a
这样操作3询问根节点到y的路径点权和时,我们询问y的进入的时间的前缀和.如果这个路径经过点x,即x是y的祖先,由于x的进入的时间早于y进入的时间,x出去的时间晚于y进入的时间,贡献会正确的加上去,否则1.如果欧拉序本来就在y之后当然不会影响.2.如果x的欧拉序在y之前,一定进入的时间和出去的时间都早于y进入的时间,对y没有贡献.
如果只有操作1,3,只需要一个树状数组即可.那来看一下操作2.将x的子树所有节点点权都+v,这个就有些难了吧.
考虑区间修改,用一个线段树维护区间点权和与区间内"进入的数量-出去的数量",每次修改的时候将x进入的时间和出去的时间这个区间打上标记v.下传标记的时候可以使得区间和+=v*"进去的数量-出去的数量".
至此,本题已经A掉了.很久没写区间修改的线段树了,竟然不知道区间修改需要懒标记...写代码20分钟,找错误30分钟,发现懒标记的问题后5分钟修改完毕.
并且提交的时候出现了上述四种情况:数组开小(欧拉序需要2n,那么线段树需要8n),没关freopen,没开long long,A掉.真是菜的真实.
long long i,tx,ty,t[100010],tv,tl,tr,flag,ttt,T,jia[800010]; long long n,m,head[100010],tot; struct edge { long long x,y,next; }e[200010]; struct node { long long l,r; }o[100010]; long long c[800010],sum[800010]; void bian(long long x,long long y) { tot++; e[tot].x=x; e[tot].y=y; e[tot].next=head[x]; head[x]=tot; } void dfs(long long x) { tot++; o[x].l=tot; for(long long j=head[x];j;j=e[j].next) { if(!o[e[j].y].l) { dfs(e[j].y); } } tot++; o[x].r=tot; } void build(long long now,long long l,long long r) { if(flag) sum[now]++; else sum[now]--; if(l==r) return; long long mid=(l+r)>>1; if(tx<=mid)build(now<<1,l,mid); else build(now<<1|1,mid+1,r); } void pushdown(long long now) { jia[now<<1]+=jia[now]; jia[now<<1|1]+=jia[now]; c[now<<1]+=sum[now<<1]*jia[now]; c[now<<1|1]+=sum[now<<1|1]*jia[now]; jia[now]=0; } void add(long long now,long long l,long long r) { c[now]+=tv; if(l==r) return ; if(jia[now]) pushdown(now); long long mid=(l+r)>>1; if(ttt<=mid)add(now<<1,l,mid); else add(now<<1|1,mid+1,r); } void qujian(long long now,long long l,long long r) { if(tl<=l&&r<=tr) { c[now]+=sum[now]*tv; jia[now]+=tv; return ; } long long mid=(l+r)/2; if(jia[now]) pushdown(now); if(tl<=mid)qujian(now<<1,l,mid); if(tr>mid)qujian(now<<1|1,mid+1,r); c[now]=c[now<<1]+c[now<<1|1]; } long long ask(long long now,long long l,long long r) { if(1<=l&&r<=tx) return c[now]; long long mid=(l+r)/2; long long tsum=0; if(jia[now]) pushdown(now); if(1<=mid)tsum+=ask(now<<1,l,mid); if(tx>mid)tsum+=ask(now<<1|1,mid+1,r); return tsum; } void check(long long now,long long l,long long r) { cout<<l<<' '<<r<<' '<<sum[now]<<' '<<c[now]<<endl; if(l==r) return ; check(now<<1,l,(l+r)/2); check(now<<1|1,(l+r)/2+1,r); } int main() { int __size__ = 20 << 20; // 20MB char *__p__ = (char*)malloc(__size__) + __size__; __asm__("movl %0, %%esp\n" :: "r"(__p__)); n=read();m=read(); for(i=1;i<=n;i++) t[i]=read(); for(i=1;i<n;i++) { tx=read();ty=read(); bian(tx,ty); bian(ty,tx); } tot=0; dfs(1); for(i=1;i<=n;i++) { tx=o[i].l; flag=1; build(1,1,tot); tx=o[i].r; flag=0; build(1,1,tot); tv=t[i]; ttt=o[i].l; add(1,1,tot); ttt=o[i].r;tv=-t[i]; add(1,1,tot); } for(i=1;i<=m;i++) { T=read(); if(T==1) { tx=read();tv=read(); ttt=o[tx].l; add(1,1,tot); ttt=o[tx].r;tv=-tv; add(1,1,tot); } else if(T==2) { tx=read();tv=read(); tl=o[tx].l;tr=o[tx].r; qujian(1,1,tot); } else //if(t==3) { tx=o[read()].l; write(ask(1,1,tot)); putchar(10); } } //check(1,1,tot); }
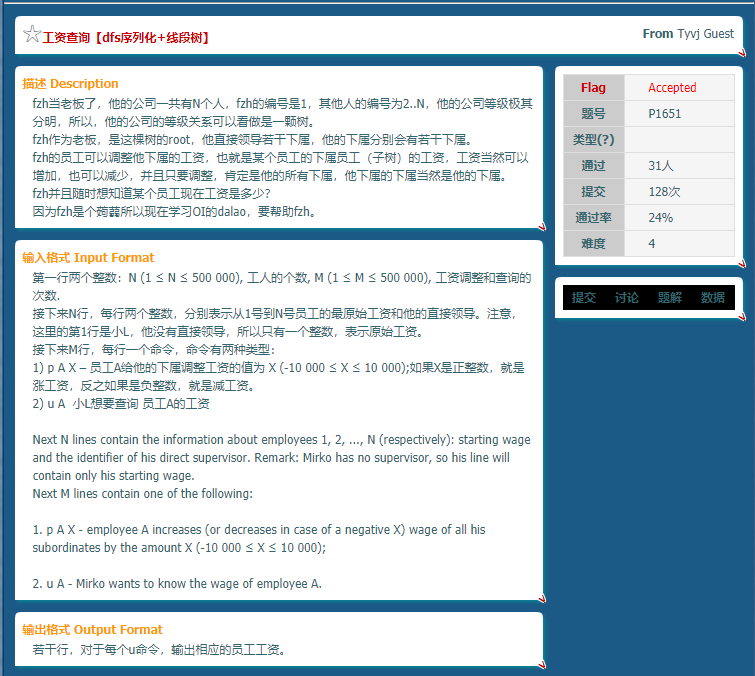
你需要支持子树修改,单点查询.我们又可以上欧拉序.那个"初始工资"看似要写一个单点修改,但是只要事先记下来,以后装作不存在,询问的时候加上去即可.
仔细思考一下后想到区间修改单点查询完全可以上一个树状数组嘛.于是一个好想好实现的代码就完成了.
long long t[500010],head[500010],tot,c[1000010]; struct edge { long long x,y,next; }e[2000010]; struct node { long long l,r; }o[500010]; inline void dfs(long long x) { tot++; o[x].l=tot; for(long long j=head[x];j;j=e[j].next) if(!o[e[j].y].l) dfs(e[j].y); tot++; o[x].r=tot; } inline long long lowbit(long long x) { return x&(-x); } inline void add(long long x,long long v) { for(;x<=tot;x+=lowbit(x)) c[x]+=v; } inline long long ask(long long x) { long long sum=0; for(;x;x-=lowbit(x)) sum+=c[x]; return sum; } int main() { long long n=read(),m=read(); t[1]=read(); for(int i=2;i<=n;i++) { t[i]=read(); long long ty=read(); e[++tot]=(edge){i,ty,head[i]}; head[i]=tot; e[++tot]=(edge){ty,i,head[ty]}; head[ty]=tot; } tot=0; dfs(1); for(;m;m--) { char op=getc(); while(op!='p'&&op!='u') op=getc(); if(op=='p') { long long tx=read();long long tv=read(); if(o[tx].l+1!=o[tx].r) { add(o[tx].l+1,tv); add(o[tx].r-1,-tv); } } else { long long xx=read(); write(ask(o[xx].l)+t[xx]); putchar(10); } } }
再看一道题:
2018年11月8号NOIP前的最后一场模拟赛T3.
输入样例 5 1 2 2 3 3 4 4 5 4 1 3 5 2 2 1 5 0 输出样例 Yes 1 2 3 5 Yes 1 5
理解题意后,脑补一下可以得到一定可以构造出<=n的解.因为我们把所有点按dfs序排一下序,第一次a1a2,a3a4,a5a6...an-1an分配,第二次按a2a3,a4a5...ana1分配,最坏也不过是覆盖树上所有边,总的距离<=2(n-1),又有抽屉原理,更短的那一个总是要<=n-1的.
我们dfs跑出dfs序,按dfs序sort一下,两次分配用lca算一下总的距离,输出小的即可.
庆祝AK啦啦啦(～￣▽￣)～
