CDQ分治,二维数点与三维数点,p1357与p2026与p2027与p2028与p2029

　　多方查找找到了2008年陈丹琪引入CDQ分治的 从《Cash》谈一类分治算法的应用.doc ,CDQ分治的名字由来也是她.

　　什么叫CDQ分治呢?来看一道二维数点题p1357.

　　

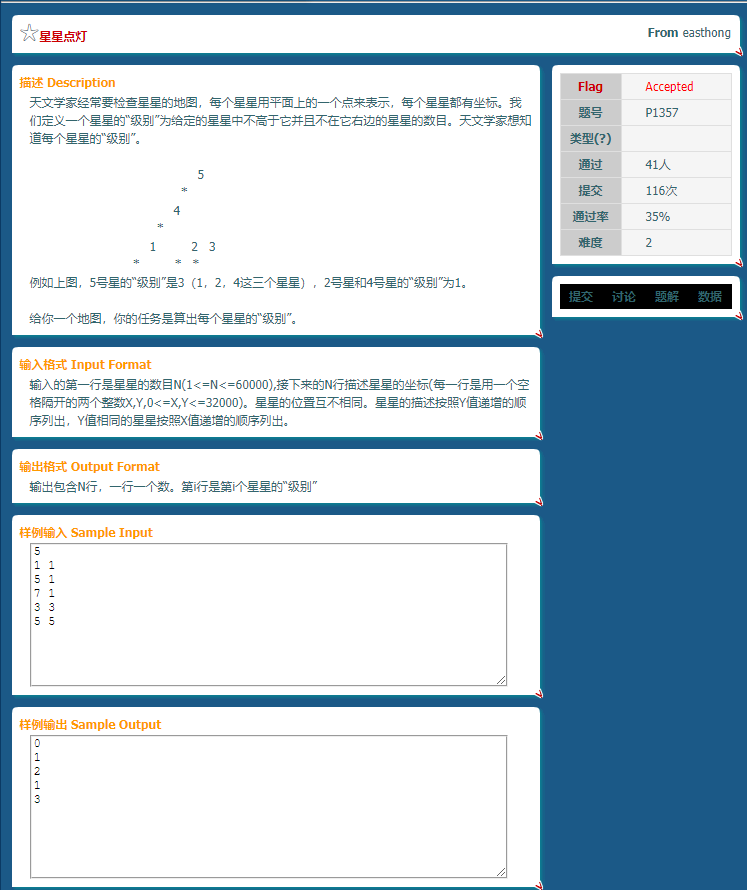
　　看了一眼题,我会树状数组!

　　现在拿它来引入CDQ分治.先全部按照x排序,由于区间[mid+1,r]不会再对区间[l,mid]有贡献,对于区间[l,r]内的贡献都可以分三步进行.

　　1.算区间[l,mid]内部相互的贡献

　　2.算区间[mid+1,r]内部相互的贡献

　　3.算[l,mid]对于[mid+1,r]的贡献

　　现在考虑如何更快的计算第3步?假设1,2步后,两个小区间内部变成了按y排序的,我们像归并一样的把两个小区间按y合并成一个大区间并得到[l,mid]对于[mid+1,r]的贡献.

　　先放一个nlog^2n的算法

bool Orz(node a,node b)
{
    return a.x<b.x;
}
void CDQ(int l,int r)
{
    if(l==r)
        return ;//自己对自己当然没贡献了
    int mid=(l+r)/2;
    CDQ(l,mid);
    CDQ(mid+1,r);
    //简陋的树状数组实现贡献统计
    for(int i=l;i<=mid;i++)//怎么还用树状数组啊?
        add(o[i].y,1);
    for(int i=mid+1;i<=r;i++)
        ans[o[i].i]+=ask(o[i].y);//算贡献
    for(int i=l;i<=mid;i++)//怎么又减回去了啊?
        add(o[i].y,-1);
    sort(o+l,o+r+1);//简陋的sort排序
}
int main()
{
    freopen("123.in","r",stdin);
    n=read();
    for(i=1;i<=n;i++)
    {
        o[i].x=read();
        o[i].y=read();
        o[i].i=i;//记录原始位置
    }
    sort(o+1,o+1+n,Orz);
    CDQ(1,n);//调用分治
    for(i=1;i<=n;i++)
        cout<<ans[i]<<endl;
}

　　再放一个好看的

struct node
{
    int x,y;
    int i;
}o[60010],temp[60010];
int ans[60010];
int i,n;
inline bool Orz(node a,node b)
{
    return a.x==b.x?a.y<b.y:a.x<b.x;
}
inline void CDQ(int l,int r)
{
    if(l==r)
        return ;//自己对自己当然没贡献了
    int mid=(l+r)/2;
    CDQ(l,mid);
    CDQ(mid+1,r);
    int a=l,b=mid+1,tot=l;
    for(;a<=mid||b<=r;tot++)//合并区间并统计答案
    {
        if(a<=mid&&o[a].y<=o[b].y||b>r)
        {
            temp[tot]=o[a];
            a++;
        }
        else 
        {
            ans[o[b].i]+=a-l;//统计答案
            temp[tot]=o[b];
            b++;
        }
    }
    for(int i=l;i<=r;i++)
        o[i]=temp[i];
}
int main()
{
    n=read();
    for(i=1;i<=n;i++)
    {
        o[i].x=read();
        o[i].y=read();
        o[i].i=i;//记录原始位置
    }
    sort(o+1,o+1+n,Orz);
    CDQ(1,n);//调用分治
    for(i=1;i<=n;i++)
    {
        write(ans[i]);
        putchar(10);
    }
}

 

　　用CDQ A掉后可以去p2026交一下.可以看到两道题几乎一样,区别在于aibi的范围.但是离散化也能写啊QAQ

 

　　

---

 

　　然后来看一个三位数点问题.

　　首先题目有些不一样了,假设随从i可以完爆f(i)个随从,本题询问的是f()=i的数量.

　　然后来做题.

　　为了继续套用CDQ的模板,我们可先按照x,y,z为第一,二,三关键字从小到大进行排序,这样可以保证任意区间[l,r]内的右区间不会对左区间产生贡献.为了O(r-l)的决策贡献,我们可以使得CDQ()两个子区间后,每个区间内部都是以y为第一关键字进行排序,然后继续按照归并排序的方法合并两个区间并计算贡献,具体计算方法也不一样了,并且y的单调性并不能保证z的单调性,我们需要树状数组了.

int i;
int n,c[200010],ans[100010],cnt[100010];
struct node
{
    int x,y,z;
    int i;
}o[100010],temp[100010];
inline int lowbit(int x)
{
    return x&(-x);
}
inline void add(int x,int k)
{
    while(x<=200000)
    {
        c[x]+=k;
        x+=lowbit(x);
    }
}
inline int ask(int x)
{
    int sum=0;
    while(x)
    {
        sum+=c[x];
        x-=lowbit(x);
    }
    return sum;
}
inline bool Orz(node a,node b)
{
    return a.x==b.x?(a.y==b.y?(a.z==b.z?a.i<b.i:a.z<b.z):a.y<b.y):a.x<b.x;
}
void CDQ(int l,int r)
{
    if(l==r)
        return ;
    int mid=(l+r)/2;
    CDQ(l,mid);
    CDQ(mid+1,r);
    int a=l,b=mid+1,tot=l; 
    for(;a<=mid||b<=r;tot++)
    {
        if(a<=mid&&(o[a].y<o[b].y||(o[a].y==o[b].y&&o[a].z<o[b].z)||(o[a].y==o[b].y&&o[a].z==o[b].z&&o[a].x<o[b].x))||b>r)
        {
            temp[tot]=o[a];
            add(o[a].z,1);
            a++;
        }
        else
        {
            ans[o[b].i]+=ask(o[b].z);
            temp[tot]=o[b];
            b++;
        }
    }
    while(a>l)
    {
        a--;
        add(o[a].z,-1);
    }
    for(tot=l;tot<=r;tot++)
        o[tot]=temp[tot];
}

int main()
{
    n=read();i=read();
    for(i=1;i<=n;i++)
    {
        o[i].x=read();
        o[i].y=read();
        o[i].z=read();
        o[i].i=i;
    }
    sort(o+1,o+1+n,Orz);
    CDQ(1,n);
    for(i=1;i<=n;i++)
        cnt[ans[i]]++;
    for(i=0;i<n;i++)
    {
        write(cnt[i]);
        putchar(10);
    }
}

　　这个代码在洛谷上仍然过不了,在本校oj上倒是跑的很好.这说明我的代码还是很糙...//2019 2 20 14:37

　　

　　不管了我们继续.

---

 

 

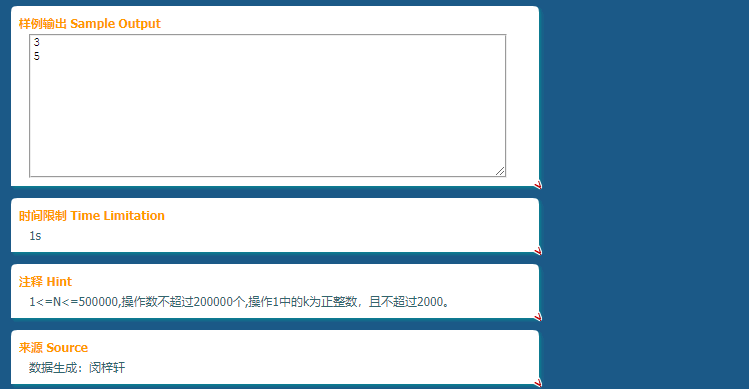
　　又有了一道CDQ.看一眼题目,是带修改的离线二维数点,如何来做呢?

　　先考虑如何读入.

　　当然是仁者见仁智者见智了.反正修改和询问是要平等的放在同一个数组(结构体)里的.我的方法是存在结构体里,并把询问拆成四个(假设x2>=x1,y2>=y1)sum(x2,y2)+sum(x1-1,y1-1)-sum(x2,y1-1)-sum(x1-1,y2).存一个i表示时间戳.并把询问的flag设为1,修改的flag设为0.

　　然后可以发现,一个区间查询sum(x,y)等价于 "查询所有时间戳小于它且x小于等于它且y小于等于它的flag=0的点的权和".这个和三维偏序好像啊,CDQ+树状数组A掉.

int i,T,tx1,tx2,ty1,ty2;
int n,tot,c[500010];
struct node
{
    int x,y;
    int i,sum;
    int flag;
}o[800010],temp[800010];//操作数*4
int lowbit(int x)
{
    return x&(-x);
}
inline void add(int x,int k)
{
    while(x<=n)
    {
        c[x]+=k;
        x+=lowbit(x);
    }
}
inline int ask(int x)
{
    int sum=0;
    while(x)
    {
        sum+=c[x];
        x-=lowbit(x);
    }
    return sum;
}
void CDQ(int l,int r)
{
    if(l==r)
        return ;
    int mid=(l+r)/2,t=l,a=l,b=mid+1;
    CDQ(l,mid);
    CDQ(mid+1,r);
    for(;a<=mid||b<=r;t++)
    {
        if(a<=mid&&o[a].x<=o[b].x||b>r)//如果a可以用且a的x小于等于b的x或b不能用
        {
            temp[t]=o[a];
            if(!o[a].flag)
                add(o[a].y,o[a].sum);
            a++;
        }
        //else if(b<=r&&o[a].x>o[b].x||a>mid)
        else//如果b的x小于a的x或a不能用
        {
            if(o[b].flag)
                o[b].sum+=ask(o[b].y);
            temp[t]=o[b];
            b++;
        }
    }
    //从上面的if可以发现y的大小不会影响答案
    for(a=l;a<=mid;a++)
        if(!o[a].flag)
            add(o[a].y,-o[a].sum);
    for(t=l;t<=r;t++)
        o[t]=temp[t];
    return ;
}
inline bool Orz(node a,node b)
{
    return a.i<b.i;
}
int main()
{
    n=read();
    for(T=read();T!=3;T=read())
    {
        tot++;
        if(T==1)
        {
            o[tot].x=read();
            o[tot].y=read();
            o[tot].sum=read();
            o[tot].i=tot;
          //o[tot].flag=0;
        }
        else
        {
            tx1=read();ty1=read();tx2=read();ty2=read();
            //下面的min,max是为了防止不合法数据..
            o[tot].x=min(tx1,tx2)-1;
            o[tot].y=min(ty1,ty2)-1;
            o[tot].i=tot;
            o[tot].flag=1;
            tot++;
            o[tot].x=max(tx1,tx2);
            o[tot].y=max(ty1,ty2);
            o[tot].i=tot;
            o[tot].flag=1;
            tot++;
            o[tot].x=max(tx1,tx2);
            o[tot].y=min(ty1,ty2)-1;
            o[tot].i=tot;
            o[tot].flag=1;
            tot++;
            o[tot].x=min(tx1,tx2)-1;
            o[tot].y=max(ty1,ty2);
            o[tot].i=tot;
            o[tot].flag=1;
        }
    }
    //这道"三维偏序"不需要事先sort了,因为有一维i有序了
    CDQ(1,tot);
    //这里的o一定是以x为第一关键字排列的,第二关键字不太清楚也不太重要
    sort(o+1,o+1+tot,Orz);//恢复原排列
    for(i=1;i<=tot;)
        if(o[i].flag)
        {
            write(o[i].sum+o[i+1].sum-o[i+2].sum-o[i+3].sum);//
            putchar(10);
            i+=4;
        }
        else
            i++;
    return 0;
}

　　

---

　　继续继续.

　　

　　

 

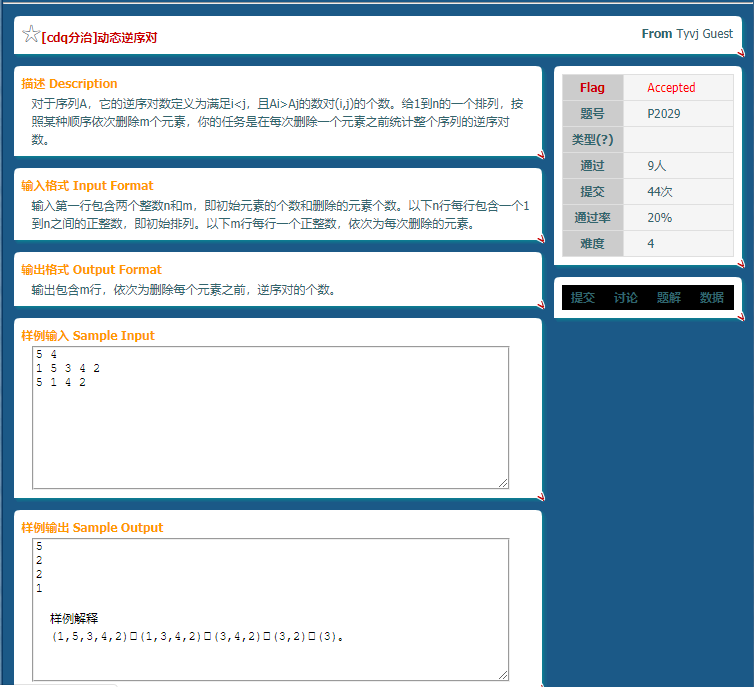
　　看到题目,逆序对?我会树状数组!

　　动态的?n^2logn!

　　我瞎说的.

　　读入的时候进行一番操作,可以继续记录每个点的权值为x,位置为i,被删除的时间戳t(最后也没被删去的设为n+1好了).那么可以算每个点的答案为.x1>x&&i1<i&&t1<=t和x1<x&&i1>i&&t1<=t的数量.可以发现t1=t的那部分重复了.我们需要一个简单容斥.这样一处理就又是三维偏序了?我们可以自豪的说出:我会CDQ!

　　具体来说,大家可以先写个n^2的暴力,过样例后再调用CDQ写个暴力,再用CDQ写个更好的算法.

　　我也会用一晚上的时间搞出多个版本放在下面.

int i,tx;
int n,m,c[100010];
inline int lowbit(int x)
{
    return x&(-x);
}
inline void add(int x,int k)
{
    while(x<=n)
    {
        c[x]+=k;
        x+=lowbit(x);
    }
}
inline int ask(int x)
{
    int sum=0;
    while(x)
    {
        sum+=c[x];
        x-=lowbit(x);
    }
    return sum;
}
struct node
{
    int x,i,t;//权值,位置,时间
    int ans;
}o[100010],temp[100010];
bool x_(node a,node b)
{
    return a.x<b.x;
}
bool t_(node a,node b)
{
    return a.t<b.t;
}
int main()
{
    freopen("123.in","r",stdin);
    n=read();m=read();
    for(i=1;i<=n;i++)
    {
        o[i].x=read();
        o[i].i=i;
        o[i].t=m+1;
    }
    sort(o+1,o+1+n,x_);
    for(i=1;i<=m;i++)
    {
        tx=read();
        o[tx].t=i;
    }
    sort(o+1,o+1+n,t_);
    for(int a=1;a<=m;a++)
    {
        for(int b=a+1;b<=n;b++)
        {
            if(o[a].x>o[b].x&&o[a].i<o[b].i||o[a].x<o[b].x&&o[a].i>o[b].i)
            {
                o[a].ans++;
            }
        }
        //cout<<o[a].ans<<endl;
    }
    for(int a=m+1;a<=n;a++)
    {
        for(int b=a+1;b<=n;b++)
        {
            if(o[a].x>o[b].x&&o[a].i<o[b].i||o[a].x<o[b].x&&o[a].i>o[b].i)
            {
                o[m+1].ans++;
            }
        }
    }
    for(i=m;i;i--)
    {
        o[i].ans+=o[i+1].ans;
    }
    for(i=1;i<=m;i++)
    {
        cout<<o[i].ans<<endl;
    }
}

int i,tx;
int n,m,c[100010];
inline int lowbit(int x)
{
    return x&(-x);
}
inline void add(int x,int k)
{
    while(x<=n)
    {
        c[x]+=k;
        x+=lowbit(x);
    }
}
inline int ask(int x)
{
    int sum=0;
    while(x)
    {
        sum+=c[x];
        x-=lowbit(x);
    }
    return sum;
}
struct node
{
    int x,i,t;//权值,位置,时间
    int ans;
}o[100010],temp[100010];
int sum;
bool x_(node a,node b)
{
    return a.x<b.x;
}
bool t_(node a,node b)
{
    return a.t<b.t;
}
void three()
{
    for(int a=1;a<=m;a++)
        for(int b=a+1;b<=n;b++)
            if(o[a].x>o[b].x&&o[a].i<o[b].i)
                o[a].ans++;
    for(int a=1;a<=m;a++)
        for(int b=a+1;b<=n;b++)
            if(o[a].x<o[b].x&&o[a].i>o[b].i)
                o[a].ans++;
  
}
void two(int l,int r)
{
    sort(o+1,o+1+n,t_);
    sort(o+l,o+r+1,x_);
    for(int a=l;a<=r;a++)
    {
        sum+=a-l-ask(o[a].i);
        add(o[a].i,1);
    }
    memset(c,0,sizeof(c));
}
int main()
{
   // freopen("123.in","r",stdin);
    n=read();m=read();
    for(i=1;i<=n;i++)
    {
        o[i].x=read();
        o[i].i=i;
        o[i].t=m+1;
    }
    sort(o+1,o+1+n,x_);
    for(i=1;i<=m;i++)
    {
        tx=read();
        o[tx].t=i;
    }
    two(m+1,n);
    sort(o+1,o+1+n,t_);
    three();
    sort(o+1,o+1+n,t_);
    o[m+1].ans=sum;
    for(i=m;i;i--)
        o[i].ans+=o[i+1].ans;
    for(i=1;i<=m;i++)
        cout<<o[i].ans<<endl;
}

int sum;
bool x_(node a,node b)
{
    return a.x<b.x;
}
bool _x(node a,node b)
{
    return a.x>b.x;
}

bool t_(node a,node b)
{
    return a.t<b.t;
}
void CDQ1(int l,int r)
{
    if(l==r)
        return ;
    int mid=(l+r)/2,a=l,b=mid+1,tot=l;
    CDQ1(l,mid);
    CDQ1(mid+1,r);
    for(;a<=mid||b<=r;tot++)
        if(a<=mid&&o[a].x<o[b].x||b>r)
        {
            o[a].ans+=b-mid-1-ask(o[a].i);
            temp[tot]=o[a];
            a++;
        }
        else
        {
            add(o[b].i,1);
            temp[tot]=o[b];
            b++;
        }
    for(b=mid+1;b<=r;b++)
        add(o[b].i,-1);
    for(tot=l;tot<=r;tot++)
        o[tot]=temp[tot];
}
void CDQ2(int l,int r)
{
    if(l==r)
        return ;
    int mid=(l+r)/2,a=l,b=mid+1,tot=l;
    CDQ2(l,mid);
    CDQ2(mid+1,r);
    for(;a<=mid||b<=r;tot++)
        if(a<=mid&&o[a].x>o[b].x||b>r)
        {
            o[a].ans+=ask(o[a].i);
            temp[tot]=o[a];
            a++;
        }
        else
        {
            add(o[b].i,1);
            temp[tot]=o[b];
            b++;
        }
    for(b=mid+1;b<=r;b++)
        add(o[b].i,-1);
    for(tot=l;tot<=r;tot++)
        o[tot]=temp[tot];
}
void three()
{
    CDQ1(1,m);
    /*for(int a=1;a<=m;a++)
        for(int b=a+1;b<=m;b++)
            if(o[a].x>o[b].x&&o[a].i<o[b].i)
                o[a].ans++;*/
    sort(o+1,o+1+n,t_);
    CDQ2(1,m);
     sort(o+1,o+1+n,t_);
   for(int a=1;a<=m;a++)
        for(int b=m+1;b<=n;b++)
            if(o[a].x>o[b].x&&o[a].i<o[b].i)
                o[a].ans++;
            
    for(int a=1;a<=m;a++)
        for(int b=m+1;b<=n;b++)
            if(o[a].x<o[b].x&&o[a].i>o[b].i)
                o[a].ans++;
}
void two(int l,int r)
{
    sort(o+1,o+1+n,t_);
    sort(o+l,o+r+1,x_);
    for(int a=l;a<=r;a++)
    {
        sum+=a-l-ask(o[a].i);
        add(o[a].i,1);
    }
    memset(c,0,sizeof(c));
}
int main()
{
    freopen("123.in","r",stdin);
    n=read();m=read();
    for(i=1;i<=n;i++)
    {
        o[i].x=read();
        o[i].i=i;
        o[i].t=m+1;
    }
    sort(o+1,o+1+n,x_);
    for(i=1;i<=m;i++)
    {
        tx=read();
        o[tx].t=i;
    }
    two(m+1,n);
    sort(o+1,o+1+n,t_);
    three();
    sort(o+1,o+1+n,t_);
    o[m+1].ans=sum;
    for(i=m;i;i--)
        o[i].ans+=o[i+1].ans;
    for(i=1;i<=m;i++)
        cout<<o[i].ans<<endl;
}

#include<iostream>
#include<iomanip>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<string>
#include<algorithm>
#include<vector>
#include<map>
#include<stack>
#include<queue>
#include<deque>
#include<set>
using namespace std;

char buf[1<<15],*fs,*ft;
inline char getc(){
  return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:* fs++;
}
inline int read(){
    int This=0,F=1; char ch=getc();
    while(ch<'0'||ch>'9'){
        if(ch=='-') F=-1;
        ch=getc();
    }
    while(ch>='0'&&ch<='9'){
        This=(This<<1)+(This<<3)+ch-'0';
        ch=getc();
    }
    return This*F;
}

inline void write(int x)
{
    if(x==0)
    {
        putchar('0');
        
        return;
    }
    if(x<0)
    {
        putchar('-');
        x=-x;
    }
    int num=0;char ch[16];
    while(x) ch[++num]=x%10+'0',x/=10;
    while(num) putchar(ch[num--]);
}
int i,tx;
int n,m,c[100010];
inline int lowbit(int x)
{
    return x&(-x);
}
inline void add(int x,int k)
{
    while(x<=n)
    {
        c[x]+=k;
        x+=lowbit(x);
    }
}
inline int ask(int x)
{
    int sum=0;
    while(x)
    {
        sum+=c[x];
        x-=lowbit(x);
    }
    return sum;
}
struct node
{
    int x,i,t;//权值,位置,时间
    int ans;
}o[100010],temp[100010];
int sum;
bool x_(node a,node b)
{
    return a.x<b.x;
}
bool _x(node a,node b)
{
    return a.x>b.x;
}

bool t_(node a,node b)
{
    return a.t<b.t;
}
void CDQ1(int l,int r)
{
    if(l==r)
        return ;
    int mid=(l+r)/2,a=l,b=mid+1,tot=l;
    CDQ1(l,mid);
    CDQ1(mid+1,r);
    for(;a<=mid||b<=r;tot++)
        if(a<=mid&&o[a].x<o[b].x||b>r)
        {
            o[a].ans+=b-mid-1-ask(o[a].i);
            temp[tot]=o[a];
            a++;
        }
        else
        {
            add(o[b].i,1);
            temp[tot]=o[b];
            b++;
        }
    for(b=mid+1;b<=r;b++)
        add(o[b].i,-1);
    for(tot=l;tot<=r;tot++)
        o[tot]=temp[tot];
}
void CDQ2(int l,int r)
{
    if(l==r)
        return ;
    int mid=(l+r)/2,a=l,b=mid+1,tot=l;
    CDQ2(l,mid);
    CDQ2(mid+1,r);
    for(;a<=mid||b<=r;tot++)
        if(a<=mid&&o[a].x>o[b].x||b>r)
        {
            o[a].ans+=ask(o[a].i);
            temp[tot]=o[a];
            a++;
        }
        else
        {
            add(o[b].i,1);
            temp[tot]=o[b];
            b++;
        }
    for(b=mid+1;b<=r;b++)
        add(o[b].i,-1);
    for(tot=l;tot<=r;tot++)
        o[tot]=temp[tot];
}
void three()
{
    CDQ1(1,m);
    /*for(int a=1;a<=m;a++)
        for(int b=a+1;b<=m;b++)
            if(o[a].x>o[b].x&&o[a].i<o[b].i)
                o[a].ans++;*/
    sort(o+1,o+1+n,t_);
    CDQ2(1,m);
     sort(o+1,o+1+n,t_);
    
    sort(o+1,o+1+m,x_);
    sort(o+1+m,o+n+1,x_);
    int a=1,b=m+1;
    for(;a<=m||b<=n;)
    {
        if(a<=m&&o[a].x<o[b].x||b>n)
        {
            o[a].ans+=b-m-1-ask(o[a].i);
            a++;
        }
        else
        {
            add(o[b].i,1);
            b++;
        }
    }
    memset(c,0,sizeof(c));
    sort(o+1,o+1+m,_x);
    sort(o+1+m,o+1+n,_x);/*
    sort(o+1,o+1+n,t_);
    for(int a=1;a<=m;a++)
        for(int b=m+1;b<=n;b++)
            if(o[a].x<o[b].x&&o[a].i>o[b].i)
                o[a].ans++;*/
    for(a=1,b=m+1;a<=m||b<=n;)
    {
        if(a<=m&&o[a].x>o[b].x||b>n)
        {
            o[a].ans+=ask(o[a].i);
            a++;
        }
        else
        {
            add(o[b].i,1);
            b++;
        }
    }
    sort(o+1,o+1+n,t_);
}
void two(int l,int r)
{
    sort(o+1,o+1+n,t_);
    sort(o+l,o+r+1,x_);
    for(int a=l;a<=r;a++)
    {
        sum+=a-l-ask(o[a].i);
        add(o[a].i,1);
    }
    memset(c,0,sizeof(c));
}
int main()
{
   // freopen("123.in","r",stdin);
    n=read();m=read();
    for(i=1;i<=n;i++)
    {
        o[i].x=read();
        o[i].i=i;
        o[i].t=m+1;
    }
    sort(o+1,o+1+n,x_);
    for(i=1;i<=m;i++)
    {
        tx=read();
        o[tx].t=i;
    }
    two(m+1,n);
    sort(o+1,o+1+n,t_);
    three();
    sort(o+1,o+1+n,t_);
    o[m+1].ans=sum;
    for(i=m;i;i--)
        o[i].ans+=o[i+1].ans;
    for(i=1;i<=m;i++)
    {
        write(o[i].ans);
        putchar(10);
    }
}

long long i,tx;
long long n,m,c[100010];
inline long long lowbit(long long x)
{
    return x&(-x);
}
inline void add(long long x,long long k)
{
    while(x<=n)
    {
        c[x]+=k;
        x+=lowbit(x);
    }
}
inline long long ask(long long x)
{
    long long sum=0;
    while(x)
    {
        sum+=c[x];
        x-=lowbit(x);
    }
    return sum;
}
struct node
{
    long long x,i,t;//权值,位置,时间
    long long ans;
}o[100010],temp[100010];
long long sum;
inline bool x_(node a,node b)
{
    return a.x<b.x;
}
inline bool _x(node a,node b)
{
    return a.x>b.x;
}
inline bool t_(node a,node b)
{
    return a.t<b.t;
}
void CDQ1(long long l,long long r)
{
    if(l==r)
        return ;
    long long mid=(l+r)/2,a=l,b=mid+1,tot=l;
    CDQ1(l,mid);
    CDQ1(mid+1,r);
    for(;a<=mid||b<=r;tot++)
        if(a<=mid&&o[a].x<o[b].x||b>r)
        {
            o[a].ans+=b-mid-1-ask(o[a].i);
            temp[tot]=o[a];
            a++;
        }
        else
        {
            add(o[b].i,1);
            temp[tot]=o[b];
            b++;
        }
    for(b=mid+1;b<=r;b++)
        add(o[b].i,-1);
    for(tot=l;tot<=r;tot++)
        o[tot]=temp[tot];
}
void CDQ2(long long l,long long r)
{
    if(l==r)
        return ;
    long long mid=(l+r)/2,a=l,b=mid+1,tot=l;
    CDQ2(l,mid);
    CDQ2(mid+1,r);
    for(;a<=mid||b<=r;tot++)
        if(a<=mid&&o[a].x>o[b].x||b>r)
        {
            o[a].ans+=ask(o[a].i);
            temp[tot]=o[a];
            a++;
        }
        else
        {
            add(o[b].i,1);
            temp[tot]=o[b];
            b++;
        }
    for(b=mid+1;b<=r;b++)
        add(o[b].i,-1);
    for(tot=l;tot<=r;tot++)
        o[tot]=temp[tot];
}
void three()
{
    CDQ1(1,m);
    sort(o+1,o+1+n,t_);
    CDQ2(1,m);
     sort(o+1,o+1+n,t_);
    sort(o+1,o+1+m,x_);
    sort(o+1+m,o+n+1,x_);
    long long a=1,b=m+1;
    for(;a<=m||b<=n;)
        if(a<=m&&o[a].x<o[b].x||b>n)
        {
            o[a].ans+=b-m-1-ask(o[a].i);
            a++;
        }
        else
        {
            add(o[b].i,1);
            b++;
        }
    memset(c,0,sizeof(c));
    sort(o+1,o+1+m,_x);
    sort(o+1+m,o+1+n,_x);
    for(a=1,b=m+1;a<=m||b<=n;)
        if(a<=m&&o[a].x>o[b].x||b>n)
        {
            o[a].ans+=ask(o[a].i);
            a++;
        }
        else
        {
            add(o[b].i,1);
            b++;
        }
    sort(o+1,o+1+n,t_);
}
void two(long long l,long long r)
{
    sort(o+1,o+1+n,t_);
    sort(o+l,o+r+1,x_);
    for(long long a=l;a<=r;a++)
    {
        sum+=a-l-ask(o[a].i);
        add(o[a].i,1);
    }
    memset(c,0,sizeof(c));
}
int main()
{
    n=read();m=read();
    for(i=1;i<=n;i++)
    {
        o[i].x=read();
        o[i].i=i;
        o[i].t=m+1;
    }
    sort(o+1,o+1+n,x_);
    for(i=1;i<=m;i++)
    {
        tx=read();
        o[tx].t=i;
    }
    two(m+1,n);
    sort(o+1,o+1+n,t_);
    three();
    sort(o+1,o+1+n,t_);
    o[m+1].ans=sum;
    for(i=m;i;i--)
        o[i].ans+=o[i+1].ans;
    for(i=1;i<=m;i++)
    {
        write(o[i].ans);
        putchar(10);
    }
}

　　最终的版本实现方式:先二维偏序sort+树状数组解决(m,n]内的贡献记在sum里 ,最后给o[m+1].ans,并用两次三维偏序解决[1,n]内部的贡献,再跑一边归并计算出(m,n]对[1,n]的贡献.逆序跑一遍后缀和后正序输出.