平衡二叉树之treap,手动随机,几次旋转,p1999与p1997
 (转自澜神PPT)
(转自澜神PPT)
普通的BST会卡,主要是由于仰仗于随机数据,如果"用心"构造数据就会被卡掉.考虑如何不被卡掉呢?我们可以"随机构建二叉树.算法导论第三版第169页-第171页有关于"一课有n个不同关键字的随机构建二叉搜索树的期望高度为lg(n)"的具体证明,有兴趣的可以看一看..所以对于离线的题,可以先随机排列这些元素,然后按照排列的顺序将他们插入树中.
如果没法同时得到所有元素,应该怎样处理呢?
treap是一课更改了节点排序方式的BST,除了键值v外,每个节点都指定一个随机数作为优先级.假设所有的优先级都不同,一个合法的treap树上键值满足BST的性质,优先级遵循堆性质.可以证明对于特定的有键值和优先级的一些数有唯一的treap与之对应.可以证明所有的操作期望运行时间是log(n).可以证明每次插入新节点时执行旋转的期望次数小于2..
treap的具体实现怎么做呢?这里用一个例题做介绍.
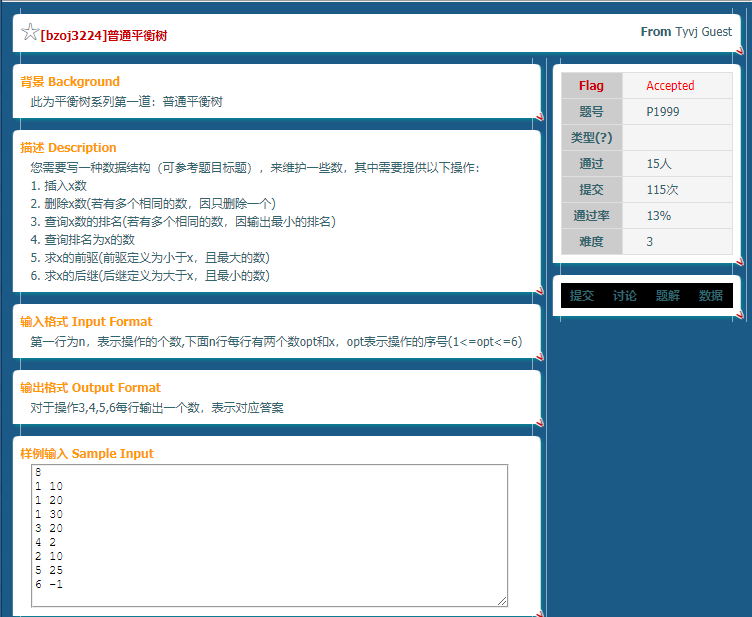
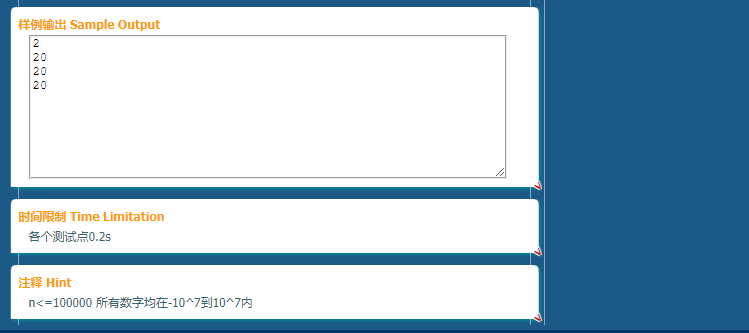
每个测试点0.2s还是丧心病狂啊.摆明了要卡快读(╯‵□′)╯︵┻━┻.也不知道普通BST能不能A.也可以发现通过率极低.
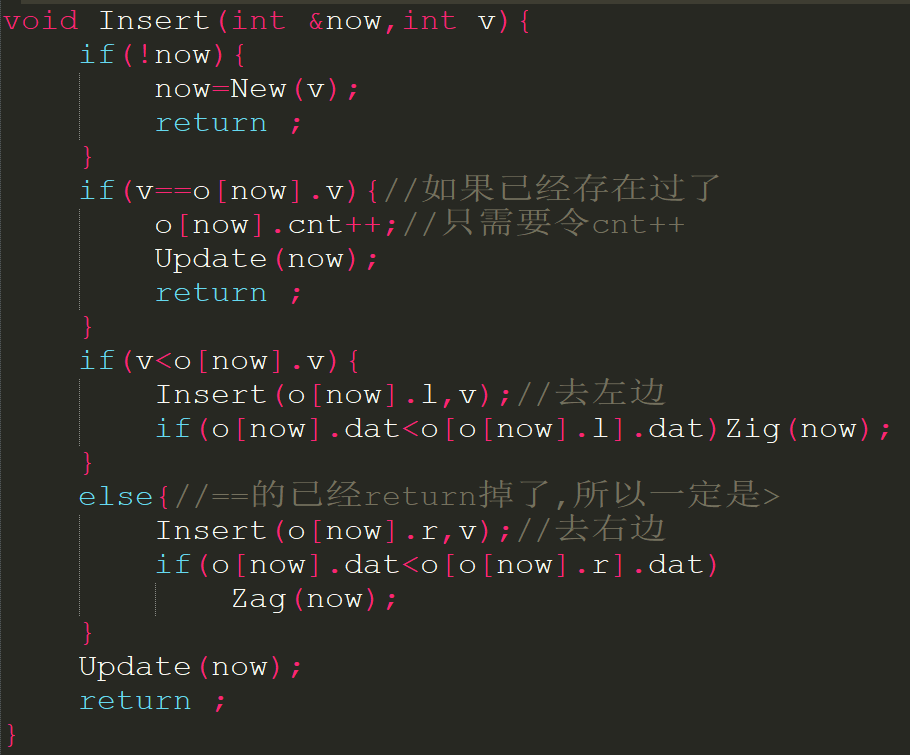
如果看了上一篇博客来直接写应该还行吧...插入删除,求前驱求后继都可写.考虑如何用键值求排名和用排名求键值?如果看了当年主席树第k大的朋友应该也能应付:维护子树的大小,如果在左子树就拐到左子树,否则拐到右子树这样子递归查询即可.但是我们想用treap写这道题,如何实现呢?
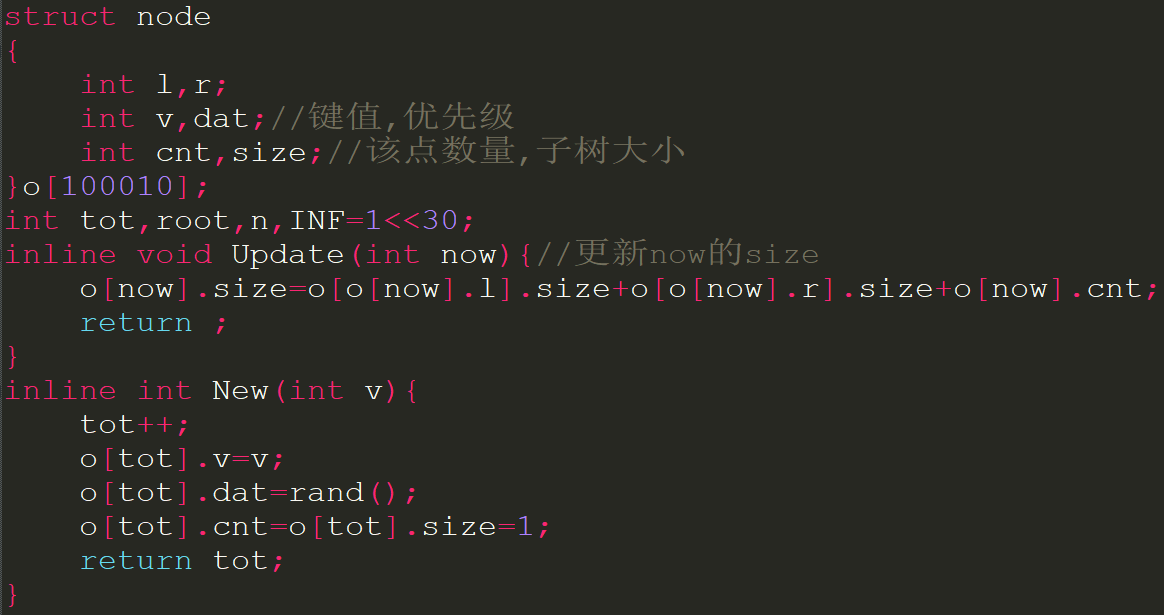
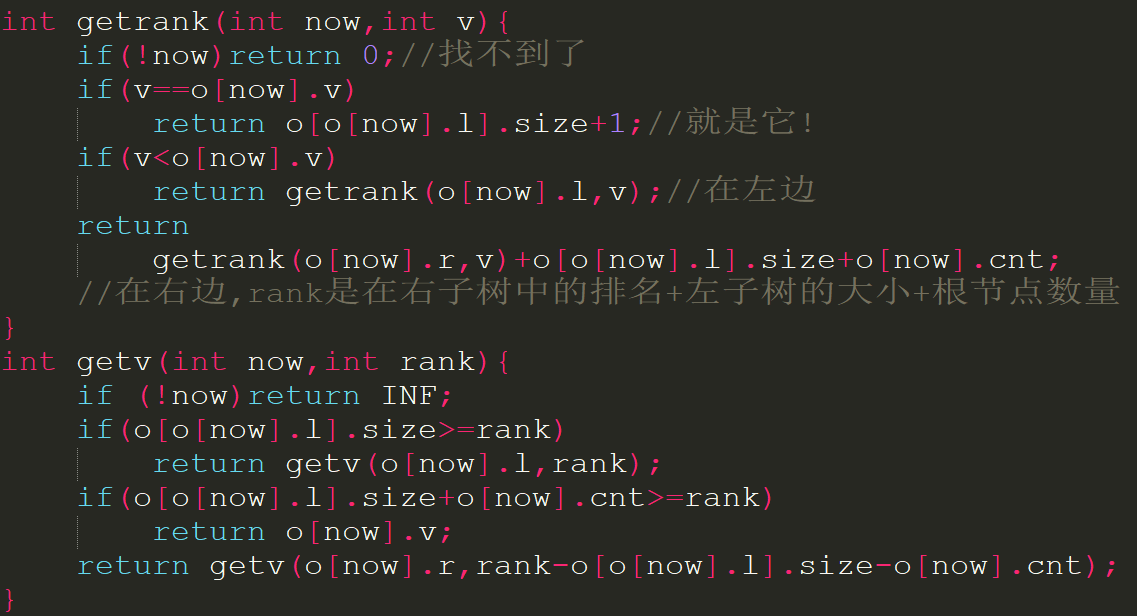
getrank()和getv()大致和主席树求第k大相似:
为了同时维护键值的二分查找树的性质与优先级的堆性质,我们引入左旋与右旋的概念.
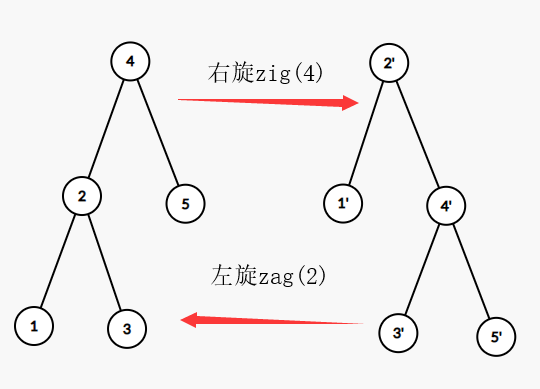
给出左右旋的作用:调用右旋zig(x)时,把x的左儿子提为自己的父亲,x做它的右儿子.同时接管它的右儿子作为自己的左儿子.左旋时把x的右儿子提为自己的父亲,做它的左儿子.同时接管左儿子作为自己的右儿子.
这样做一下之后,BST的性质没有改变.对于堆性质来说,只有2,4的上下相对位置改变.可以用来维护堆性质.
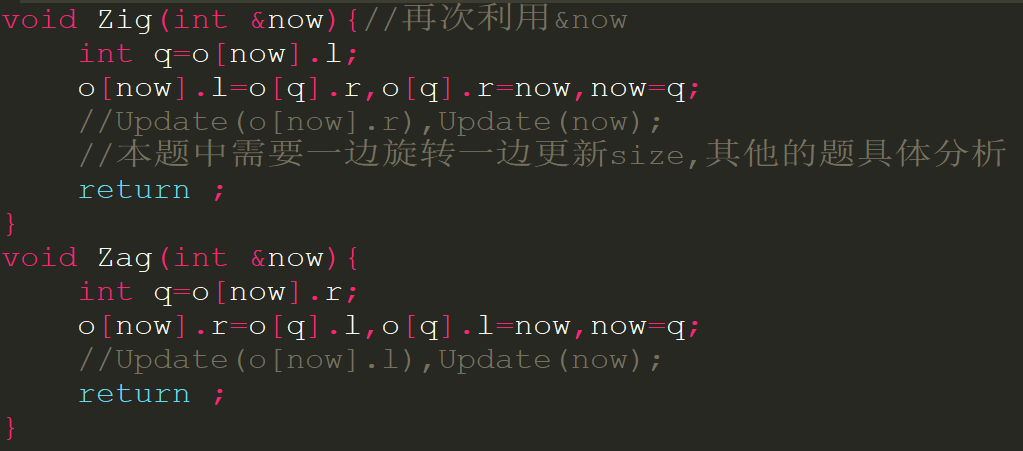
然后就可以开心的进行插入操作了.每次对于一个v,rand一个随机数作为优先级,先插入,如果优先级有问题就转一下~
然后就又来到了删除的环节...这回我们可以利用旋转,找到后直接向下旋转直到把它弄到树的叶子层,然后用&now把自己弄成0,它的父亲记录自己位置的l或r也为0了,就相当于已经被扔掉了每次都觉得好悲伤.具体实现能否用get下标()函数呢?考虑到删除后还要更新祖先的size,不如写递归函数.好像用while也可以写,主要是因为懒. 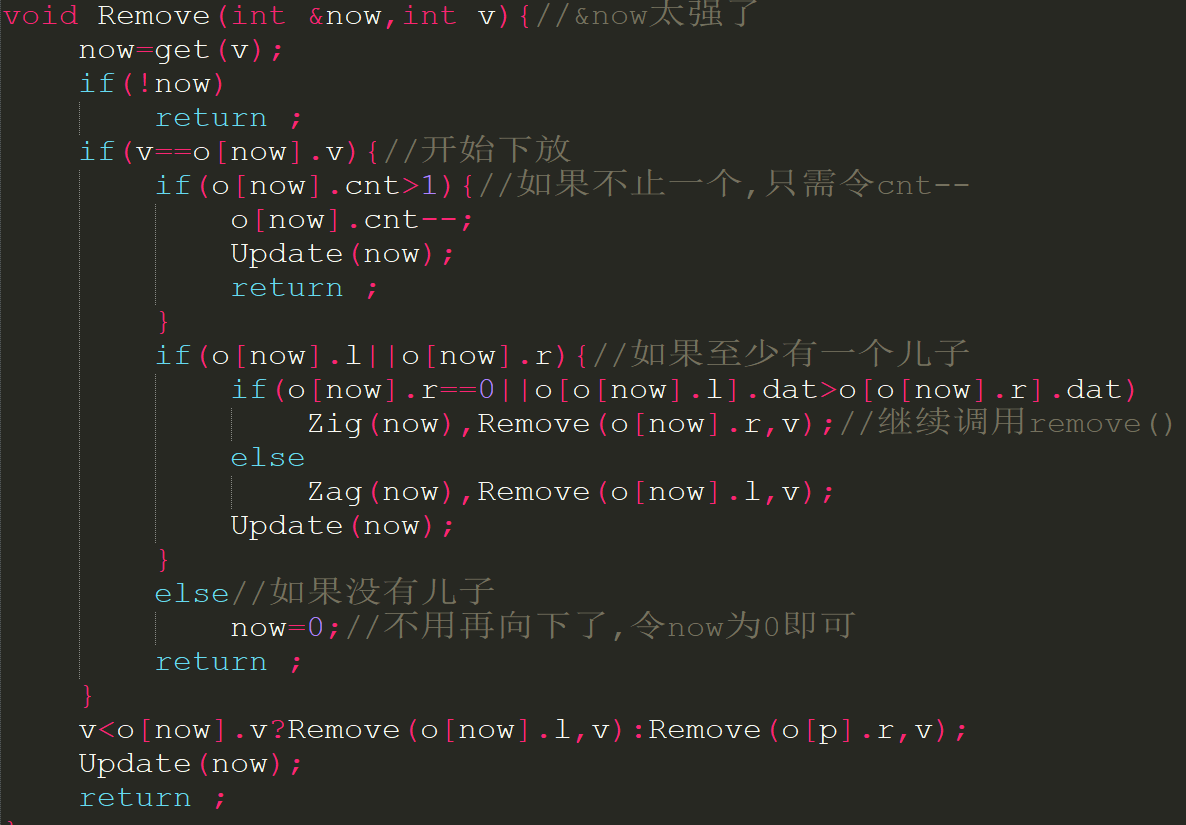
求前驱后继什么的都与之前类似了,也不涉及树的更新.这里不给代码.

struct node { int l,r; int v,dat; int cnt,size; }a[100010]; int tot,root,n,INF=1<<30; inline int New(int v) { a[++tot].v=v; a[tot].dat=rand(); a[tot].cnt=a[tot].size=1; return tot; } inline void Update(int now) { a[now].size=a[a[now].l].size+a[a[now].r].size+a[now].cnt; return ; } void Build() { New(-INF),New(INF); root=1;a[1].r=2; Update(root); return ; } int Getrank(int now,int v) { if(now==0)return 0; if(v==a[now].v) return a[a[now].l].size+1; if(v<a[now].v)return Getrank(a[now].l,v); return Getrank(a[now].r,v)+a[a[now].l].size+a[now].cnt; } int Getv(int now,int rank) { if (now==0)return INF; if(a[a[now].l].size>=rank)return Getv(a[now].l,rank); if(a[a[now].l].size+a[now].cnt>=rank)return a[now].v; return Getv(a[now].r,rank-a[a[now].l].size-a[now].cnt); } void Zig(int &now) { int q=a[now].l; a[now].l=a[q].r,a[q].r=now,now=q; Update(a[now].r),Update(now); return ; } void Zag(int &now) { int q=a[now].r; a[now].r=a[q].l,a[q].l=now,now=q; Update(a[now].l),Update(now); return ; } void Insert(int &now,int v) { if(now==0) { now=New(v); return ; } if(v==a[now].v) { a[now].cnt++;Update(now); return ; } if(v<a[now].v) { Insert(a[now].l,v); if(a[now].dat<a[a[now].l].dat)Zig(now); } else { Insert(a[now].r,v); if(a[now].dat<a[a[now].r].dat)Zag(now); } Update(now); return ; } int Getpre(int v) { int ans=1;int now=root; while(now) { if(v==a[now].v) { if(a[now].l>0) { now=a[now].l; while(a[now].r>0)now=a[now].r; ans=now; } break; } if(a[now].v<v&&a[now].v>a[ans].v)ans=now; now=v<a[now].v?a[now].l:a[now].r; } return a[ans].v; } int Getnext(int v) { int ans=2,now=root; while(now) { if(v==a[now].v) { if(a[now].r>0) { now=a[now].r; while(a[now].l>0) now=a[now].l; ans=now; } break; } if(a[now].v>v&&a[now].v<a[ans].v)ans=now; now=v<a[now].v?a[now].l:a[now].r; } return a[ans].v; } void Remove(int &now,int v) { if(now==0) return ; if(v==a[now].v) { if(a[now].cnt>1) { a[now].cnt--,Update(now); return ; } if(a[now].l||a[now].r) { if(a[now].r==0||a[a[now].l].dat>a[a[now].r].dat) Zig(now),Remove(a[now].r,v); else Zag(now),Remove(a[now].l,v); Update(now); } else now=0; return ; } v<a[now].v?Remove(a[now].l,v):Remove(a[now].r,v); Update(now); return ; } int topt,tx; int main() { //freopen("123.in","r",stdin); Build(); for(n=read();n;n--) { topt=read();tx=read(); switch(topt) { case 1: Insert(root,tx); break; case 2: Remove(root,tx); break; case 3: write(Getrank(root,tx)-1); break; case 4: write(Getv(root,tx+1)); break; case 5: write(Getpre(tx)); break; case 6: write(Getnext(tx)); break; } } return 0; }


再来看一道题~
看一眼操作,好像都很熟悉但是又都不会.好像可以上主席树.但是这里强行让你上平衡树该怎么做呢?假如所有询问更改区间都是[1,n]你会不会呢?正是上一题.考虑如何做这道题呢?我们需要线段树套平衡树
先开一个线段树,每个区间都是一个treap. 建树的时候枚举所有的数一个个插入线段树中.而且真正存线段树的数组是没有的,因为它只维护该区间的treap的根节点而已. 对于操作1,k的排名等价于小于k的数+1,可以用线段树在整块的区间内求出小于k的个数求和后输出+1,复杂度期望log(n)^2. 对于操作2,我们可以利用操作1进行二分求解.即二分答案x,每个x都log(n)^2求解区间内的排名,如果离散化是可以做到log(n)^3.(当时没想到离散化,log(n)变log(1e8)). 对于操作3,可以删除后insert,和相当于普通平衡树操作1+操作2. 对于操作4,求前驱显然可以在区间内求出前驱并取max. 对于操作5,求后继可以在区间内求出后继并取min.
我的代码常数很大,但是n,m都不太大,评测机还开了2s,所以才A掉.
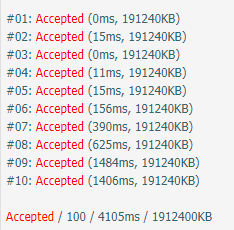
所以说树套树并没有那么恐怖了,不就是两百多行代码么.

#define inf 2000000007 using namespace std; int n,m,ans,tot; struct node{ int l,r; int dat,v; int size,cnt; }o[4000010]; int root[200010],a[200010]; void Update(int now){ o[now].size=o[o[now].l].size+o[o[now].r].size+o[now].cnt; return; } void Zig(int &now){ int p=o[now].l; o[now].l=o[p].r; o[p].r=now; o[p].size=o[now].size; Update(now); now=p; return; } void Zag(int &now){ int p=o[now].r; o[now].r=o[p].l; o[p].l=now; o[p].size=o[now].size; Update(now); now=p; return; } void Insert(int &now,int v){ if(!now){ tot++; now=tot; o[now].size=o[now].cnt=1; o[now].v=v; o[now].dat=rand(); return; } o[now].size++; if(v==o[now].v){ o[now].cnt++; return ; } if(v<o[now].v){ Insert(o[now].l,v); if (o[o[now].l].dat<o[now].dat) Zig(now); } else{ Insert(o[now].r,v); if(o[o[now].r].dat<o[now].dat) Zag(now); } return; } void del(int &now,int x){ if(now==0) return; if(o[now].v==x){ if(o[now].cnt>1) o[now].cnt--,o[now].size--; else{ if(o[now].l==0||o[now].r==0) now=o[now].l+o[now].r; else if(o[o[now].l].dat<o[o[now].r].dat) Zig(now),del(now,x); else Zag(now),del(now,x); } return ; } x>o[now].v?del(o[now].r,x):del(o[now].l,x); Update(now); return ; } void add(int now,int l,int r,int x,int v) { Insert(root[now],v);//线段树内只需要存root //在 以root[now]为树根的树中加入v if (l==r) return; int mid=(l+r)>>1;now=now<<1; if(x<=mid) add(now,l,mid,x,v); else add(now+1,mid+1,r,x,v); return; } void rankplus(int now,int v){ if (!now)return; if (v==o[now].v)ans+=o[o[now].l].size; else if(v<o[now].v)rankplus(o[now].l,v); else{ ans+=o[o[now].l].size+o[now].cnt; rankplus(o[now].r,v); } return; } void getrank(int now,int l,int r,int x,int y,int v){ if(l==x&&r==y){//对于整块的 rankplus(root[now],v); return; } int mid=(l+r)>>1;now=now<<1; if (y<=mid) getrank(now,l,mid,x,y,v); else if (x>mid) getrank(now|1,mid+1,r,x,y,v); else getrank(now,l,mid,x,mid,v),getrank(now|1,mid+1,r,mid+1,y,v); return; } void getv(int x,int y,int v){ //二分答案! int l=0,r=1e8,res; while(l<=r){ int mid=(l+r)>>1; ans=1; getrank(1,1,n,x,y,mid); if(ans<=v){ l=mid+1; res=mid; } else r=mid-1; } write(res); return; } void modify(int now,int l,int r,int x,int yl,int xz){ del(root[now],yl); Insert(root[now],xz); if (l==r) return; int mid=(l+r)>>1; if (x<=mid)modify(now<<1,l,mid,x,yl,xz); else modify(now<<1|1,mid+1,r,x,yl,xz); return; } void qianqu(int now,int v){ if (!now) return; if (o[now].v<v){ ans=max(ans,o[now].v); qianqu(o[now].r,v); } else qianqu(o[now].l,v); return; } void getbefore(int now,int l,int r,int x,int y,int v) { if (l==x&&r==y){ qianqu(root[now],v); return; } int mid=(l+r)>>1;now=now<<1; if (y<=mid) getbefore(now,l,mid,x,y,v); else if (x>mid) getbefore(now+1,mid+1,r,x,y,v); else getbefore(now,l,mid,x,mid,v),getbefore(now+1,mid+1,r,mid+1,y,v); return; } void houji(int now,int v) { if(!now)return; if(o[now].v>v){ ans=min(o[now].v,ans); houji(o[now].l,v); } else houji(o[now].r,v); return; } void getafter(int now,int l,int r,int x,int y,int v) { if (l==x&&r==y){ houji(root[now],v); return; } int mid=(l+r)>>1; if (y<=mid) getafter(now<<1,l,mid,x,y,v); else if (x>mid) getafter(now<<1|1,mid+1,r,x,y,v); else getafter(now<<1,l,mid,x,mid,v),getafter(now<<1|1,mid+1,r,mid+1,y,v); return; } int main(){ n=read(),m=read(); for (int i=1;i<=n;i++) a[i]=read(),add(1,1,n,i,a[i]);//在第i个位置加入a[i] while(m--) { int flag=read(),x,y,k; switch(flag) { case 1:x=read(),y=read(),k=read(),ans=1,getrank(1,1,n,x,y,k),write(ans);break; case 2:x=read(),y=read(),k=read(),getv(x,y,k);break; case 3:x=read(),y=read(),modify(1,1,n,x,a[x],y),a[x]=y;break; case 4:x=read(),y=read(),k=read(),ans=0,getbefore(1,1,n,x,y,k),write(ans);break; case 5:x=read(),y=read(),k=read(),ans=inf,getafter(1,1,n,x,y,k),write(ans);break; } } }
说起来,真的有人可以在考场上写出来树套树么...恐怖如斯




