BST 万事开头难

 

　　万事开头难,只要开始做就会比不做会的多.

　　爆零真的不开心.

　　BST,Binary Search Tree,二叉搜索树.它可以做一个类似字典树,支持插入某个键值,询问某个键值的权值,删去某个键值.也可以做一个类似于优先队列的东西,查询区间最大值,区间最小值,一个键值v的前驱(小于v的最大的键值)后继(大于v的最小的键值)等等.开更多数组可以维护更多的信息.这里结合算法导论与算法竞赛进阶指南讲解如何初步完成这些操作.

---

 　　首先它是一个二叉树,并且节点的左子树节点的键值都小于该节点.右子树的节点的键值都大于它.因此可以想象到即使对于相同的信息,可以表现出来的合法的BST也很多,大概是卡塔兰数吧,具体证明略.现在考虑如何用这种数据结构.

　　这里用结构体建树...

 

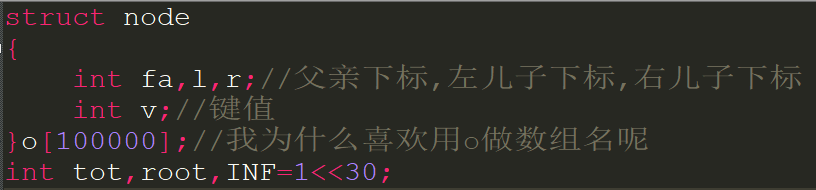
　　root表示根节点下标.虽然大部分时间根节点都应该是1,但是如果根节点被删除或者以后被旋转什么的,就需要把根节点换一下,所以需要记录.

　　为了避免越界,减少边界情况的特殊判断,可以一开始就建立插入两个键值为-∞与+∞的节点.

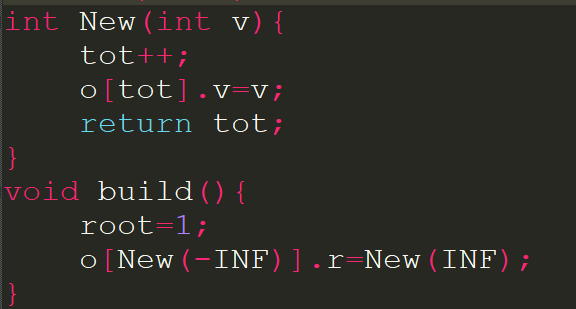
　　调用函数build()后的BST长这个样子

　　这样建树的结果是什么呢?我也不太清楚.

　　先不说插入与删除.假如有了一个合法的BST,如何.查询某个键值是否存在并如果存在返回下标呢?可以考虑用函数递归或者一个循环搞定.

　　

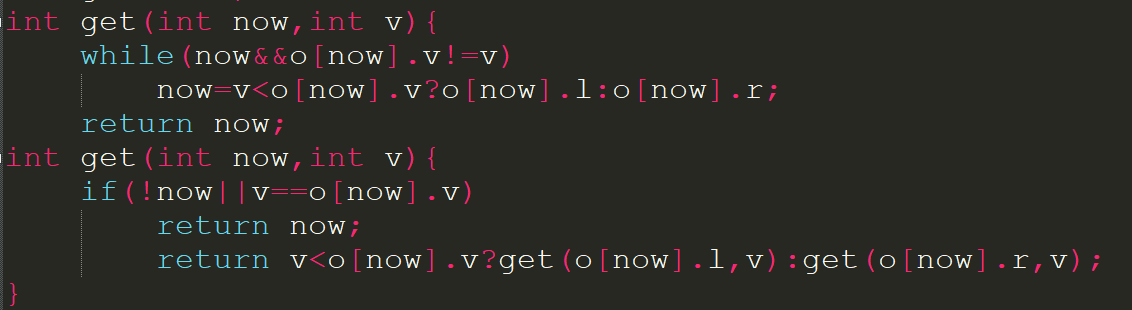
　　主函数内调用get(root,tv)即可.这两个get常常循环比较快,但是递归起来比较好理解...如果想查询以x为下标的节点的子树内是否有tv也可以调用get(x,tv);也可以发现v是一成不变的,实际应用时也可以写全局变量,不传进去v.

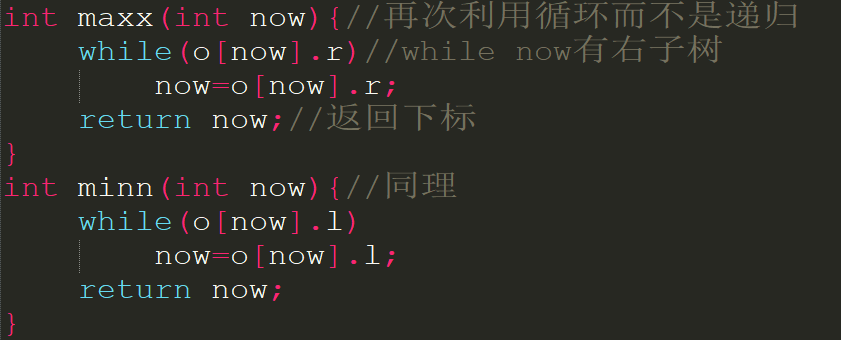
　　如何查询树内键值的最大最小值?如果没有删除操作可以int声明两个个数O(1)修改O(1)查询,但是删除时就需要再次查找.不如写一个函数每次O(h)查询(h表示BST的高度)(这里把复杂度均摊的思想会多次用到.如何把修改O(n)查询O(1)变成修改查询O(logn)是以后经常遇见的).考虑BST的定义,显然每次贪心向下查找即可.比如maxx操作只需贪心的选择当前节点的右子树.

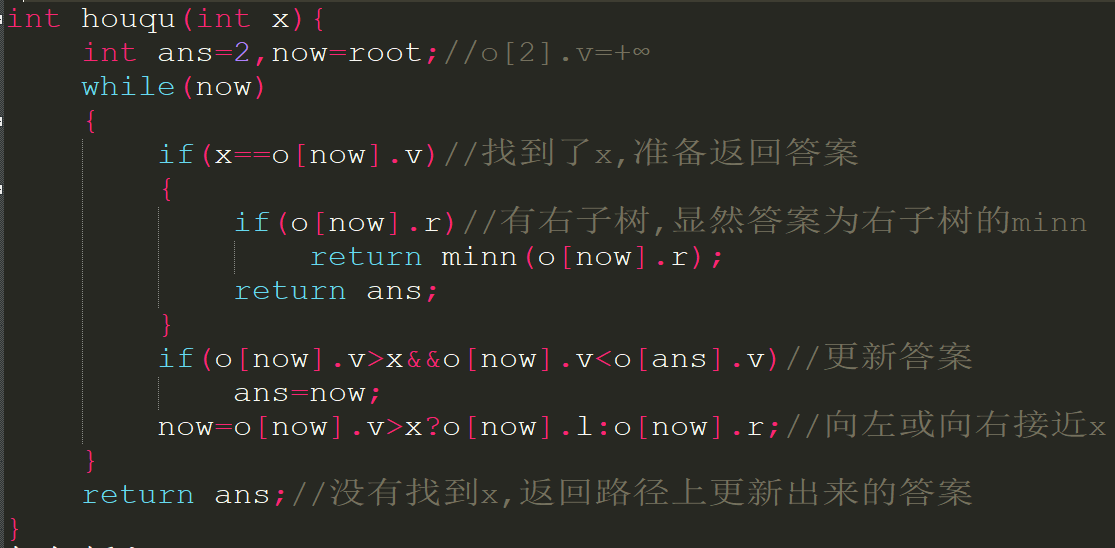
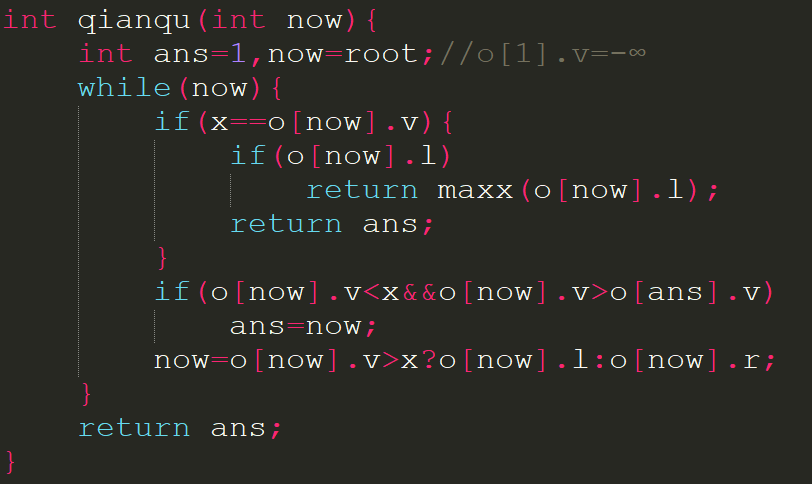
　　如何查询一个数的前驱与后继?(具体定义在上面)还是根据性质,为了求x的后驱,可以从根节点向下走去找键值x,一边走一边更新答案.如果找到了x,答案应该在路上或者是x的右子树的minn.否则就是路上.

　　为什么插入与删除最后说呢?因为删除太麻烦了...

　　考虑如何插入和删除.可以利用get()找到是否存在并在主函数函数插入,但是也可以利用&now进行操作.三目运算符真好用.　　

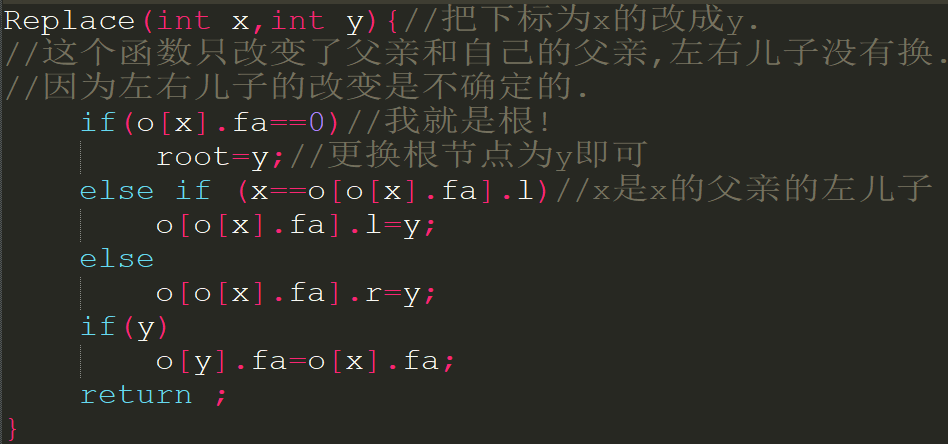
　　为啥删除麻烦呢?因为把一个数删掉还不够,你有可能需要找一个儿子来代替它.一下全部选择让右儿子来代替.

　　突然换行,表示重视如果它没有儿子,单独一人,直接把它的父亲对它的联系切断即可.如果有一个儿子,只需要让这个儿子顶替自己.如果两个儿子呢?希望能让自己的后继顶替自己.因为希望越少变动越好.而后继一定在自己的右子树里且没有左儿子,我们希望后继单独来顶替自己,同时后继的左儿子带着左儿子的子树顶替后继,这样的新树一定是合法的.

　　介绍两种方法:

　　

 　　

　

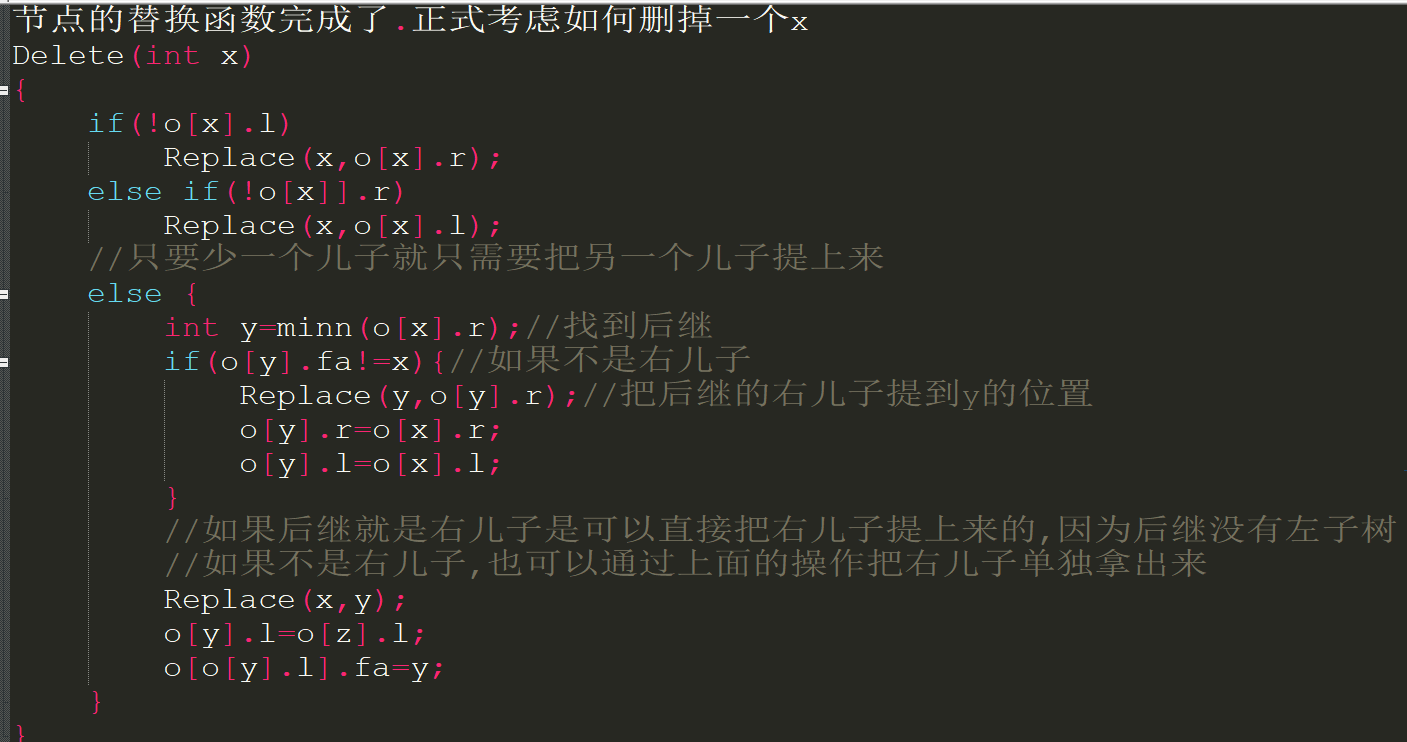
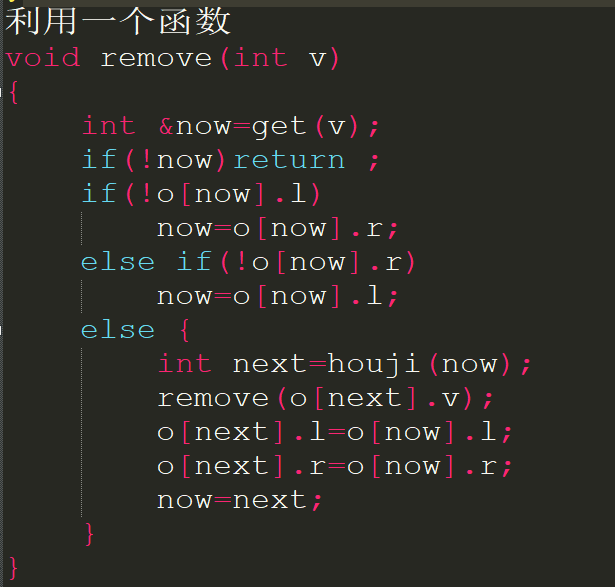
　　如果数据随机,这样生成的BST期望高度为logn,每次查询和修改复杂度是也是logn..但是总有一些凉心出题人构造一些数据卡普通BST,比如从小到大依次插入,所形成的BST深度是n的,操作的复杂度页为n.我们需要学习更高级的BST.但不是今天.