tarjan与无向图连通性----割点割边连通分量

　　noip集训前天天爆零,为了勉励自己,决定如果再爆零我就开始学tarjan,然后第二天果然没爆零.

　　总之tarjan对我来说是很难的.

　　考虑割点割边:割点是一个点,删去后图会分裂成两个以上不相连的子图.割边同理,只删去这个边后图会分裂乘两个以上不相连的子图.这个玩意非常重要,所以经常要用到.如何在线性时间内找到割点与割边呢?Robert Tarjan站了出来.你以后或者已经经常听到这个名字了.很多算法都叫tarjan算法.

　　现在从一个图的任意一点进入对图进行dfs遍历,每个点都访问一次,按照这个搜索的顺序设立"时间戳",设为dfn[i],用到的边和所有的点显然可以构成一个dfs搜索树.然后我们再引入一个追溯值low[i]表示 以i为根的树中的节点和能通过一条不在搜索树上的边到达子树的节点的dfn最小值.如果原来的图就是一个树,那么每个节点的low[i]显然=dfn[i].代码实现的时候我们dfs的同时贪心维护一下就行.

　　有了这两个数组后,我们可以一边跑dfs一边判断割边割点了.一个边e[i]是桥,当且仅当搜索树上存在x的一个子节点y满足dfn[e[i].x]<low[e[i].y].因为当这个子树与外界不连通时x作为一个根节点,它的dfn应该小于大家的low.如果dfn[x]>=low[y]证明y可以通过除了i别的边到达x或者x以前的位置,就不是一个桥了.

　　上面只是简单的无重边的割边...考虑无向图,由于双向建边,每个点都能"看到"自己的父亲,用它来更新自己的low,然后就大家都是桥了.这个时候可以通过记录每个节点的父节点fa来解决,只不允许用自己的父亲更新自己.然而当有重边的时候,有一条仍然不能用父亲更新自己,但其他的边却可以,他们都不是割边.但是只记录一下父亲会导致大家都不能更新,大家都是割边.有什么解决办法呢?可以记录进入每个节点的时候的那个边的下标,然后利用下标^1的操作,使得x不能利用fa更新自己的low.问题解决.

　　

 

 

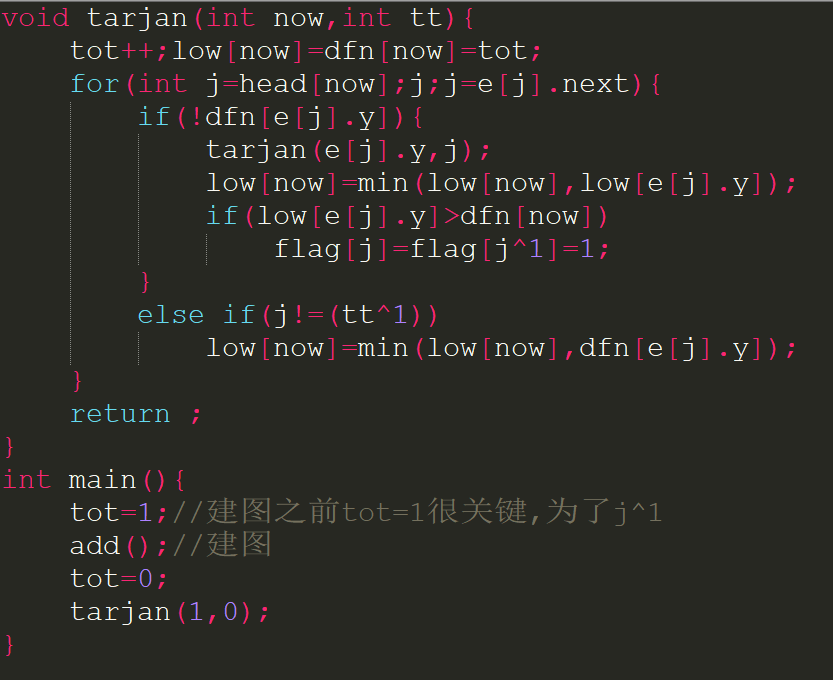
　　考虑割点的判定.点x是割点当且仅当存在x的子节点(树上)y:dfn[x]<=low[y].当x是dfs起点的时候需要存在两个节点满足上式.证明大概和上面一样,感性理解一下即可.考虑到dfn[x]<=low[y],可以不用管重边了.

　　

 

　　

 　　那么联通分量是什么呢?如果一个无向联通图不存在割点,称它是一个点双联通图.如果不存在割边,称它是一个边双联通图.这种情况并不多,我们继续定义:一个图的极大点双联通子图称为点双联通分量,极大边双联通子图被称为边双联通分量.也就是说,这里的联通分量是相对于整体的一个子图.这里的"极大"表示不存在在这个子图的基础上增加点后还是一个双联通子图.比如一个点双联通图只有一个点双联通分量----它自己.

　　一个无向联通图是点双联通图,当且仅当点数<=2或任意两点都同时包含在至少一个环中.

点数<=2很显然吧,就这么些个点,删去也没用.
如果每任意两点x,y都在同一个环内,删去其他节点z,z不在环内就不影响联通性,即使在环内,xy仍可以通过环上的另一条路径相连.既然删去z后任意两点都仍然联通,那么就不会形成两个子图,充分性得证.
如果无向联通图内存在xy不同时处于一个环内,且它是一个点双联通图.来证明它的必要性.考虑这里环的定义:一个不自交的简单环.那么xy联通且不在一个环内,说明要么只有一条路径,要么有>=2的路径有相同的交点.只有一条路径的话,删去路径上的一点会使得xy失去联通性.有相同交点时删去这个交点,xy仍会失去联通性.

　　一个无向联通图是边双联通图,当且仅当任意一条边都存在于一个简单环中.

这回不需要点数小于等于2的了.如果点数为1,没有边代表着没有边不存在于简单环中,也算是了.如果点数为2,只有一条边显然是割边,有重边时大家都可以互相组成简单环,没有一个是重边.总之是都可以用"任意一条边都存在于一个简单环中"来概况一下.
考虑更一般的情况.
若每个边都存在于简单环中,删去它仍不能使任何两个点失去联通性,充分性得证.
如果有环不存在于简单环中,也就是说它的两个端点只有它自己一条边相连.把它删去,至少它的两个端点就失去了联通性,不是一个边双联通图.必要性得证.

 　　证明完后,来考虑如何求联通分量?

　　边联通分量内部一定没有桥,一个无向联通图删去所有桥后剩下的子图都是边联通分量,一个点也是一个边双联通分量.按着这个思想,先跑出来所有的桥,再dfs好多下,不经过桥,标记路过的节点就行了.

　　

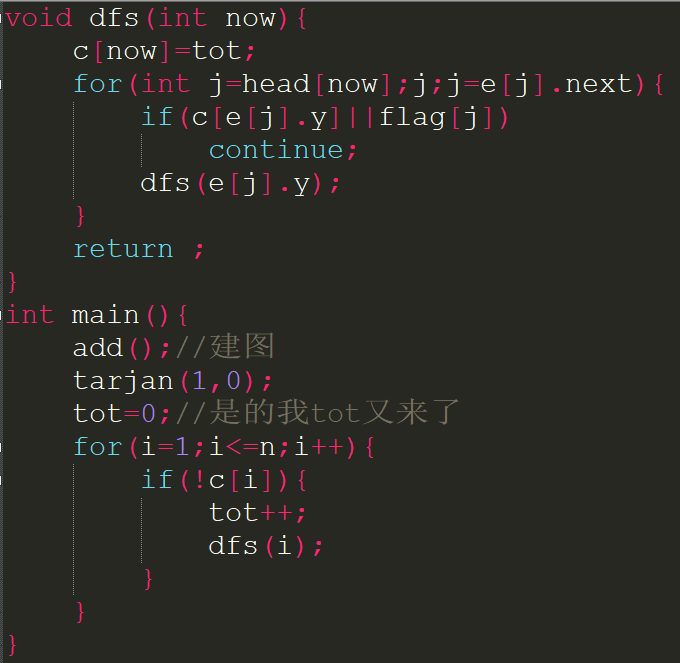
　　做完边联通分量的判定后还可以做一个很重要的事:缩点.把每个边联通分量看作一个节点,枚举每条边,如果两端点的c[]不一样就可以c[x]c[y]之间连边了.

　　

　　点双联通分量又是很难弄.因为割点可以在多个点双联通分量中出现.,就不能直接的不用割点把图拆分.

　　比如

　　

 

　　2是一个割点,但2_3和2_1都是点双联通分量.这个时候就需要vectot了,因为事先不知道每个分量的大小和数量,想开二维数组但是一般不能开n^2的数组.

　　具体的实现方法:

1.当元素第一次被访问时把它入栈.
2.当dfn[x]<=low[y]时,从栈顶不断弹出节点,直到y被弹出来(y一定事先在栈里了.把这些节点作为一个点双联通分量放在vector内.

　　

 

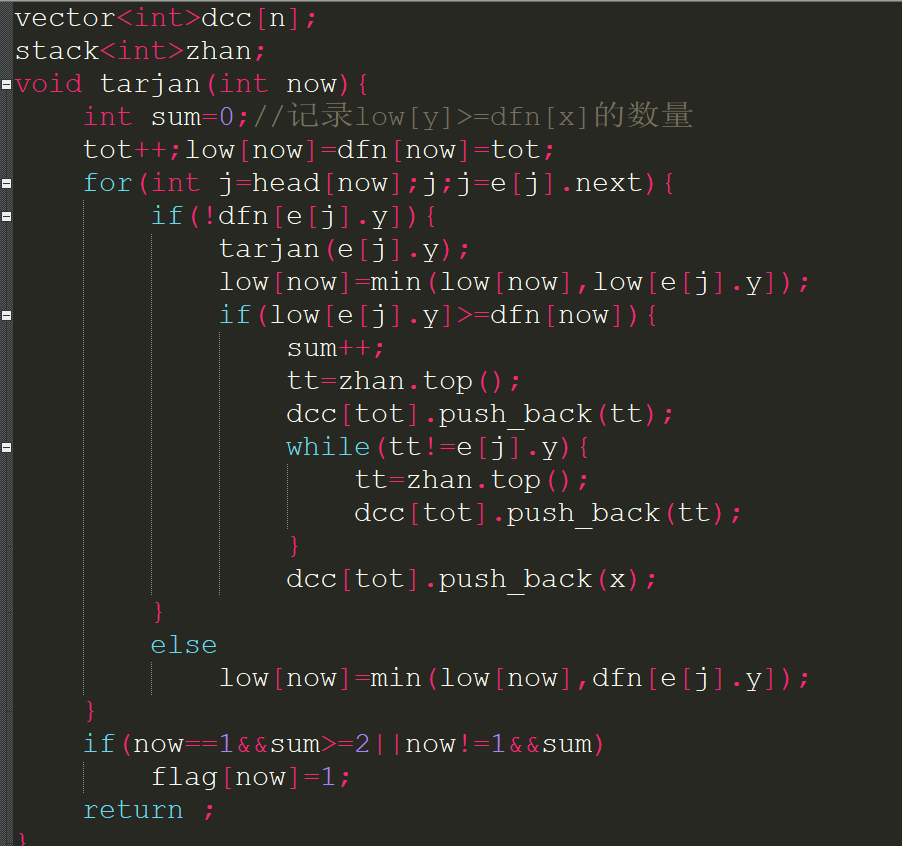
　　点双联通的缩点,需要把所有的点联通分量和割点都给拉出来作为新图的节点.考虑最后形成的图,割点之间一定是没有连边的,也就是说只要对所有点联通分量和割点进行连边即可.

　　

 　　

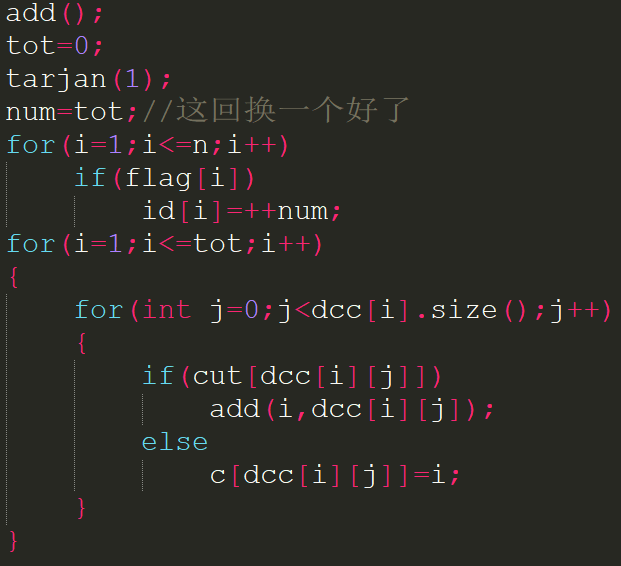
　　tarjan就先这样,以后遇到题了再说.