常见的概率分布

1. 离散型分布

1.1 两点分布（伯努利分布/贝努利分布/0-1分布）

称随机变量 \(X\) 服从参数为 \(p\) 的伯努利分布，如果它分别以概率 \(p\) 和 \(1-p\) 取 1 和 0 为值。​

\[P(X=k)=p^k(1-p)^{1-k}, \quad k=0,1\\ X\sim B(1,p)\\ E(X)=p\\ D(X)=p(1-p) \]

1.2 二项分布

n次独立的伯努利试验。如果事件发生的概率是 \(p\)，n次独立重复试验中发生k次的概率是（有放回抽样）

\[P(X=k)=\mathrm C_n^k p^k(1-p)^{n-k},\quad k=0,1,...,n\\ X\sim B(n,p)\\ E(X)=np\\ D(X)=np(1-p) \]

有 \(n\) 件产品，其中 \(m\) 件次品 (\(m<n\))，从中不放回地任意抽取 \(k\) 件产品和有放回地任意抽取 \(k\) 件产品，在这两种抽取方法中每次抽出次品的概率相同，都为 \(\frac{m}{n}\)，抽得次品数的期望值也相同，都为 \(k\frac{m}{n}\)，但抽到的次品数的分布列不同，方差不同（超几何分布与二项分布）

关于为什么不放回抽样每次抽出次品的概率相同，见文末。

1.3 几何分布

在n次伯努利试验中，试验k次才第一次成功的概率。几何分布是帕斯卡分布当 \(r=1\) 时的特例

\[P(X=k)=(1-p)^{k-1}p,\quad k=1,2,...\\ X \sim GE(p)\\ E(X)=\frac{1}{p}\\ D(X)=\frac{1-p}{p^2} \]

例：某产品的合格率为0.05，则首次查到不合格品的检查次数 \(X\sim GE(0.05)\)

1.4 帕斯卡分布（负二项分布）

在重复独立的伯努利试验中，设每次试验成功的概率为 \(p\)，若将试验进行到出现 \(r\) (\(r\) 为常数) 次成功为止，以随机变量 \(X\) 表示所需试验次数，

\[P(X=k)=\mathrm C_{k-1}^{r-1}p^r(1-p)^{k-r}, \quad k=r,r+1,...\\ E(X)=\frac{r}{p} \]

（当 \(r\) 是整数时，负二项分布又称帕斯卡分布）

1.5 超几何分布

从 N 个物件中抽出 n 个物件，成功抽出指定种类的物件的次数（不放回抽样）。

\(X\sim H(N,M,n)\)

产品抽样检查中，假定在 N 件产品中有 M 件不合格品，即不合格率为 \(\frac{M}{N}\)，在产品中随机抽 n 件进行检查，发现 k 件不合格品的概率为

\[P(X=k)=\frac{\mathrm C_M^k \mathrm C_{N-M}^{n-k}}{\mathrm C_N^n},\quad k=0,1,...,min\{n,M\}\\ E(X)=\frac{nM}{N}\\ D(X)=n\frac{M}{N}(1-\frac{M}{N})\frac{N-m}{N-1} \]

1.6 泊松分布

泊松分布适用于描述单位时间内随机事件发生的次数，泊松分布的参数 \(\lambda\) 是单位时间内随机事件的平均发生次数。

\[P(X=k)=\frac{\lambda^k}{k!}e^{-\lambda}, \quad k=0,1,...\\ E(X)=\lambda\\ D(X)=\lambda \]

特征函数：\(\Psi(t)=\exp\{\lambda(e^{it}-1)\}\)

2. 连续型分布

2.1 均匀分布 \(U(a,b)\)

密度函数：

\[f(x)=\left\{ \begin{aligned} &\frac{1}{b-a}&,&\quad a<x<b \\ &0&,&\quad 其他 \end{aligned} \right. \]

分布函数：

\[F(x)=\left\{ \begin{aligned} &0&,&\quad x<a \\ &\frac{x-a}{b-a}&,&\quad a\leq x < b\\ &1&,&\quad x\geq b \end{aligned} \right. \]

期望和方差：

\[E(X)=\frac{a+b}{2}\\ D(X)=\frac{(b-a)^2}{12} \]

2.2 指数分布 \(E(\lambda)\)

\[f(x)=\left\{ \begin{aligned} &\lambda e^{-\lambda x} &,&\quad x>0 \\ &0&,&\quad 其他 \end{aligned} \right. \]

\[F(x)=\left\{ \begin{aligned} &0&,&\quad x<0\\ &1-e^{-\lambda x} &,&\quad x\geq0 \\ \end{aligned} \right. \]

\[E(X)=\frac 1\lambda\\ D(X)=\frac {1}{\lambda^2} \]

2.3 正态分布 \(N(\mu, \sigma^2)\)

\[f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}},\quad -\infty <x<+\infty\\ F(x)=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^x e^{-\frac{(t-\mu)^2}{2\sigma^2}}dt\\ \]

\[E(X)=\mu\\ D(X)=\sigma^2 \]

一般来说，正态分布的密度曲线是以为中心，在 \(\mu\) 的两侧呈对称的形状，曲线的形状像一个钟的剖面，故称为钟形曲线。 \(\sigma\) 越大，密度曲线的峰度越低； \(\sigma\) 越小，密度曲线的峰度越高。无论参数 \(\mu\) 和 \(\sigma\) 取何值，密度曲线下所覆盖的面积均于 1。 正态分布的密度曲线见图 1.4 。

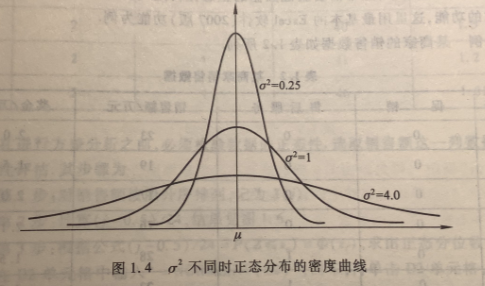
正态分布曲线下，位于\(\mu\pm \sigma, \mu\pm 2\sigma, \mu\pm 3\sigma\) 之间的面积分别约占总面积的 68.26%，95.45%， 99.73%， 如 图 1.5 所示 。

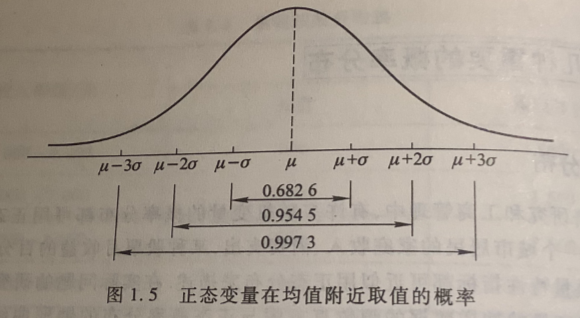
当总体概率分布为正态分布时，作为从中抽出的样本，其统计量的样本概率分布有卡方分布，t分布，F分布等。因此正态分布成为计量经济学乃至统计学中最重要的概念之一。

2.4 \(\chi^2\)分布

如果从标准正态分布 \(N(0,1)\) 的总体中得到 n 个独立的随机变量分别为 \(X_1, X_2, ..., X_n\)，则由 \(\sum_{i=1}^n X_i^2\) 得到的分布称作自由度为 n 的 \(\chi^2\) 分布，记为 \(X\sim \chi^2(n)\).

期望和方差：

\[E(X)=n\\ D(X)=2n \]

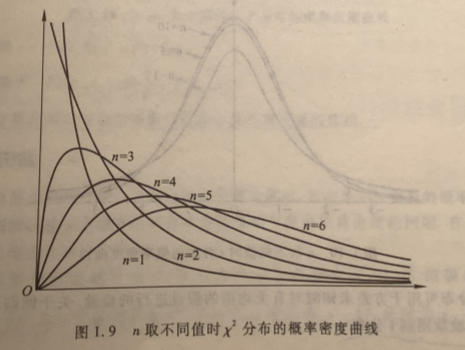
\(\chi^2\) 分布的加法定理. 设 \(X_1, X_2, ..., X_k\) 是相互独立的随机变量，且 \(X_i\sim \chi^2(n_i), i=1,2,...,k\)，则

\[\sum_{i=1}^k X_i \sim \chi^2(n_1+n_2+...+n_k). \]

\(\chi^2\)分布与 \(N(0,1)\) 分布之间有如下关系：

设 \(X_1, X_2, ..., X_n\) 是相互独立的随机变量，并且 \(X_i\sim N(0,1), i=1,2,...,n\)，则

\[\sum_{i=1}^n X_i^2\sim \chi^2(n). \]

2.5 t分布

设随机变量 \(X\sim N(0,1), Y\sim \chi^2(n)\)，X 与 Y 相互独立，则随机变量

\[t=\frac{X}{\sqrt{Y/n}} \]

遵从自由度为n的t分布，记为 \(t=\frac{X}{\sqrt{Y/n}}\sim t(n)\).

期望和方差：

当n>2时，\(E(t)=0, D(t)=\frac{n}{n-2}\).

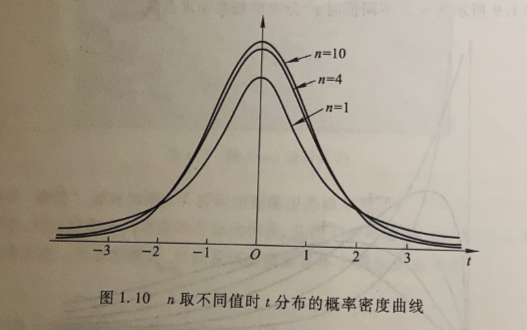
当n<30时，t分布的分散程度比标准正态分布大，密度函数曲线比较平缓，随着n的增大，t分布逐渐接近标准正态分布；当 \(n\rightarrow\infty\)时，t分布渐进标准正态分布

t分布可用于方差未知时对有关均值的假设进行检验。关于回归系数的显著性检验就用到 t分布。

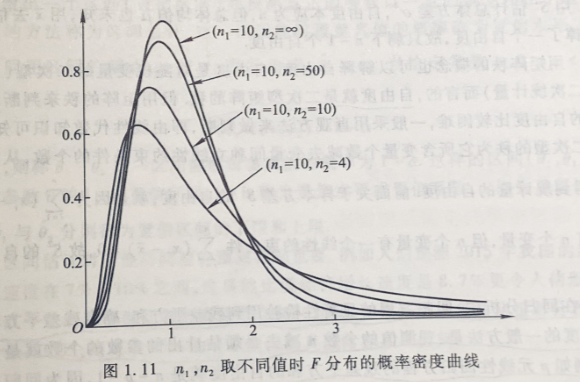
2.6 F分布

设随机变量 \(X\sim \chi^2(n_1), Y\sim \chi^2(n_2)\)，且X与Y相互独立，则称随机变量

\[F=\frac{X/n_1}{Y/n_2} \]

遵从自由度为 \((n_1,n_2)\) 的F分布，记作 \(F\sim F(n_1,n2)\).

F分布的形状为正偏态分布，随着 \(n_1,n_2\) 的增大，其概率密度曲线的偏斜度虽有所减缓却仍保持偏态分布，并不以正态分布为其极限分布形式。

如果 \(t\sim t(n)\)，则 \(t^2\sim F(1,n)\)；
如果 \(F\sim F(n_1,n_2)\)，则 \(\frac1F \sim F(n_2, n_1)\).

F分布在回归方程的显著性检验中具有重要作用

3. 补充：关于不放回抽样

为什么不放回抽样每次抽到次品的概率都是 \(\frac{m}{n}\)，因为不放回抽样，每次抽样，都是与前些次的抽样相关的，从相关性上，前面的人抽中，与抽不中，对后面都有影响，但是这种影响又相互抵消。

例如，有 10 件产品，其中 3 件次品，7件正品，不放回的取，求第3次取得次品的概率。应用全概率公式：

同理计算可得，第一次取得次品的概率与第二次取得次品的概率都是 \(\frac{3}{10}\)
这就叫抽签原理

n个签，其中有m个是“上”签，第一个人抽到“上”签的概率是m/n，第k个人抽到“上”签的概率也是m/n
前提是：每个人都不知道前面人的抽签结果，如果知道的话，就不是这样了
这也就说明了抽签先后顺序是不影响概率的，是公平的

---

参考：
https://blog.csdn.net/IMWTJ123/article/details/79979120
https://blog.csdn.net/holly_Z_P_F/article/details/107556675