关于熵，条件熵，交叉熵等的介绍

参考：
《数学之美》
一文搞懂交叉熵在机器学习中的使用，透彻理解交叉熵背后的直觉
详解机器学习中的熵、条件熵、相对熵和交叉熵
常用的分类问题中的损失函数

1.信息量与信息熵

香农在他著名的论文”通信的数学原理“（A Mathematic Theory of Communication）中提出了”信息熵“的概念，解决了信息的度量问题，并且量化出信息的作用。

一条信息的信息量与其不确定性有着直接的关系。比如说，我们要搞清楚一件非常非常不确定的事，或是我们一无所知的事情，就需要了解大量的信息。相反，如果已对某件事了解较多，则不需要太多的信息就能把它弄清楚。从这个角度来看，可以认为，信息量就等于不确定性的多少（即与事件发生的概率有关）。当越不可能的事件发生了，我们获取到的信息量就越大，越可能发生的事件发生了，我们获取到的信息量就越小。

那么如何量化信息量的度量呢？来看一个例子。2014年举行了世界杯足球赛，大家都很关心谁会是冠军。假如我错过了看世界杯，赛后我问一个知道比赛结果的观众“哪支球队是冠军"？他不愿意直接告诉我，而让我猜，并且我每猜一次，他要收一元钱才肯告诉我是否猜对了，那么我要掏多少钱才能知道谁是冠军呢？我可以把球队编上号，从1到32，然后提问：“冠军球队在1一16号中吗？”假如他告诉我猜对了，我会接着问：“冠军在1一8号中吗？”假如他告诉我猜错了，我自然知道冠军队在9一16号中。这样只需要五次，我就能知道哪支球队是冠军。所以，谁是世界杯冠军这条消息的信息量只值5块钱。

当然，香农不是用钱，而是用“比特”（Bit）这个概念来度量信息量。一个比特是一位二进制数，在计算机中，一个字节就是8比特。在上面的例子中，这条消息的信息量是5比特。（如果有朝一日有64支球队进入决赛阶段的比赛，那么“谁是世界杯冠军"的信息量就是6比特，因为要多猜一次。）读者可能已经发现，信息量的比特数和所有可能情况的对数函数log有关。（\(log_232=5,log_264=6\)）

【信息量的定义】假设 \(X\) 是一个随机变量，其取值集合为\(\chi\)，概率分布函数 \(p(x)=Pr(X=x), x\in\chi\)，则定义事件 \(X=x_0\) 的信息量为：

\[I(x_0)=-log(p(x_0)) \]

对于某随机事件，每一种可能性可以计算出一个信息量，而熵用来表示所有信息量的期望。

有些读者会发现实际上可能不需要猜五次就能猜出谁是冠军，因为像西班牙、巴西、德国、意大利这样的球队夺得冠车的可能性比日本、南非、韩国等球队大得多。因此，第一次猜测时不需要把32支球队等分成两个组，而可以把少数几支最可能的球队分成一组，把其他球队分成另一组。然后猜冠军球队是否在那几支热门队中。重复这样的过程，根据夺冠概率对余下候选球队分组，直至找到冠军队。这样，也许三次或四次就猜出结果。因此，当每支球队夺冠的可能性（概率）不等时，“谁是世界杯冠军”的信息量比5比特少。香农指出，它的准确信息量应该是

\[H=-(p_1logp_1+p_2logp_2+...+p_{32}logp_{32}) \]

其中，\(p_1,p_2,...,p_{32}\)分别是这32支球队夺冠的概率。香农把它称为“信息熵”（Entropy），一般用符号 \(H\) 表示，单位是比特。当32支球队夺冠概率相同时，对应的信息熵等于5比特。可以证明上面公式的值不可能大于5，即

\[0 \leq H \leq logn \]

【熵的定义】对于任意一个随机变量 \(X\)（比如得冠军的球队），它的熵定义如下：

\[\begin{align*} H(X)&=-\sum _{x\in X}p(x)logp(x)\\ &= -\sum_{i=1}^n p(x_i)logp(x_i) \end{align*} \]

对于只有两种取值的0-1分布问题，熵的计算方法可以简化为：

\[H(X)=-p(x)logp(x)-(1-p(x))log(1-p(x)) \]

将一维随机变量分布推广到多维，可以得到联合熵（joint entropy）为：

\[\begin{align*} H(X,Y)&=-\sum_{x,y}p(x,y)logp(x,y)\\ &=-\sum_{i=1}^n\sum_{j=1}^mp(x_i,y_i)logp(x_i,y_i) \end{align*} \]

变量的不确定性越大，熵也就越大，要把它搞清楚，所需信息量也就越大。

2.条件熵

有些时候，在战争中1比特的信息能抵过干军万马。在第二次世界大战中．当纳粹德国兵临前苏联莫斯科城下时，斯大林在欧湖已经无兵可派，他们在西伯利亚的中苏边界却有60万大军不敢使用，因为苏联人不知道德国的轴心国盟友日本当时的军事策略是北上进攻前苏联，还是南下和美国开战。如果是南下，那么苏联人就可以放心大胆地从亚洲撤回60万大军增援莫斯科会战。事实上日本人选择了南下，其直接行动是后来的偷袭珍珠港，但是苏联人并不知骁。斯大林不能猜，因为猜错了后果是很严重的。这个“猜“既是指扔钢镚儿似的卜卦，也包括主观的臆断。最后传奇间谍佐尔格向莫斯科发去了信息量仅1比特却价值无限的情报（信息）：“日本将南下"，于是前苏联就把西伯利亚所有的军队调往了欧洲战场。后面的故事大家都知道了。

如果把这个故事背后的信息论原理抽象化、普遍化，可以总结如下：

一个事物（比如上面讲到的日本内阁的战略决定）内部会存有随机性，也就是不确定性，假定为 \(U\)，而从外部消除这个不确定性唯一的办法是引入信息 \(I\)，而需要引入的信息量取决于这个不确定性的大小，即 \(I>U\) 才行。当 \(I<U\) 时，这些信息可以消除一部分不确定性，也就是说新的不确定性：

\[U'=U-I \]

反之，如果没有信息，任何公式或数字的游戏都无法排除不确定性。几乎所有的自然语言处理、信息与信号处理的应用都是一个消除不确定性的过程。

网页搜索本质上就是要从大量（几十亿个）网页中．找到和用户输入的搜索词最相关的几个网页。几十亿种可能性，当然是很大的不确定性 \(U\)。如果只剩下几个网页，就几平没有了不确定性了（此时 \(U'<<U\)），甚至是完全确定了（对于导航类搜索就是如此，第一条结果通常就是要找的网页）。因此，网页搜索本质上也是利用信息消除不确定性的过程。如果提供的信息不够多，比如搜索词是常用的关键词，诸如“中国”、“经济”之类的，那么会有好多相关的结果，用户可能还是无从选择，这时正确的做法是挖掘新的隐含信息，比如网页本身的质量信息。如果这些信息还是不够消除不确定性，不妨再问问用户。这就是相关搜索的理论基础。不正确的做法是在这个关键词上玩数字和公式的游戏，由于没有额外的信息引入，这种做法没有效果，这就是很多做搜索质量的人非常辛苦却很少有收获的原因。最糟糕的做法是引入人为的假设，这和“蒙“没什么差别。其结果是似平满足了个别用户的口味，但是对大部分用户来讲，搜索结果反而变得更糟。合理利用信息，而非玩弄什么公式和机器学习算法，是做好搜索的关键。

知道的信息越多，随机事件的不确定性就越小。

这些信息，可以是直接针对我们要了解的随机事件，也可以是和我们关心的随机事件相关的其他（事件）的信息一一通过获取这些相关信息也能帮助我们了解所关注的对象。比如自然语言的统计模型，其中的一元模型就是通过某个词本身的概率分布来清除不确定因素；而二元及更高阶的语言模型则还使用了上下文的信息，那就能准确预测一个句子中当前的词汇了。在数学上可以严格地证明为什么这些”相关的“信息也能够消除不确定性，为此，需要引入一个条件熵（Conditional Entropy）的概念。

假定 \(X\) 和 \(Y\) 是两个随机变量， \(X\) 是我们需要了解的。假定我们现在知道了 \(X\) 的随机分布 \(P(X)\)，那么也就知道了 \(X\) 的熵:

\[H(X)=-\sum_{x\in X}P(x)logP(x) \]

那么它的不确定性就是这么大。现在假定我们还知道 \(Y\) 的一些情况，包括它和 \(X\) 一起出现的概率，在数学上称为联合概率分布，以及在 \(Y\) 取不同值的前提下 \(X\) 的概率分布，在数学上称为条件概率分布。

【条件熵的定义】条件熵 \(H(X|Y)\) 定义为\(Y\)给定条件下\(X\)的条件概率的熵对\(Y\)的数学期望：

\[\begin{align*} H(X|Y)&=\sum_yp(y)H(X|Y=y)\\ &=-\sum_up(y)\sum_xp(x|y)logp(x|y)\\ &=-\sum_x\sum_yp(x,y)logp(y|x)\\ &=-\sum_{x,y}p(x,y)logp(y|x) \end{align*} \]

可以证明， \(H(X)\geq H(X|Y)\)，即多了 \(Y\) 的信息之后，关于 \(X\) 的不确定性下降了。在统计语言模型中，如果把 \(Y\) 看成前一个字，那么在数学上就证明了二元模型的不确定性小于一元模型。同理，可以定义有两个条件的条件熵

\[H(X|Y,Z)=-\sum_{x\in X,y\in Y,z\in Z}p(x,y,z)logp(x|y,z) \]

还可以证明， \(H(X|Y)\geq H(X|Y,Z)\)。也就是说，三元模型应该比二元好。

上述的等号什么时候成立？等号成立说明增加了信息，不确定性却没有降低。如果我们获取的信息与要研究的事物毫无关系，等号就成立。（下一节中介绍互信息时也会讲到）

另外，还可以证明条件熵 \(H(X|Y)=H(X,Y)-H(Y)\)。证明如下：

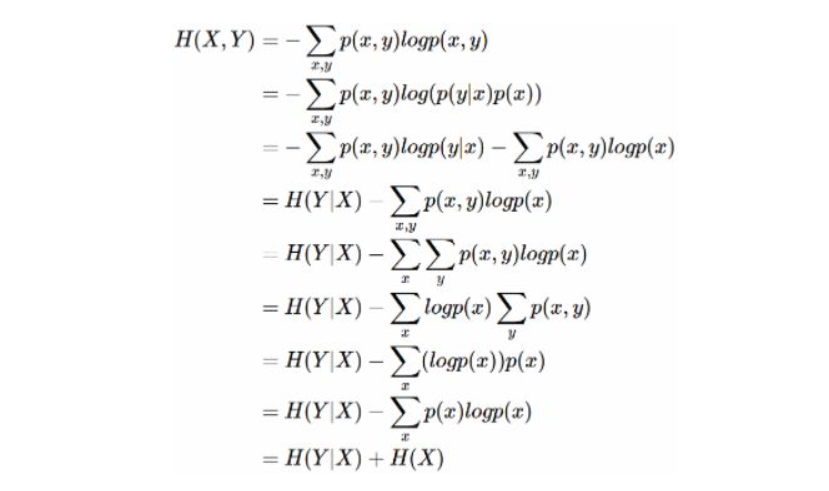
举个例子，比如环境温度是低还是高，和我穿短袖还是外套这两个事件可以组成联合概率分布 \(H(X,Y)\)，因为两个事件加起来的信息量肯定是大于单一事件的信息量的。假设 \(H(X)\) 对应着今天环境温度的信息量，由于今天环境温度和今天我穿什么衣服这两个事件并不是独立分布的，所以在已知今天环境温度的情况下，我穿什么衣服的信息量或者说不确定性是被减少了。当已知 \(H(X)\) 这个信息量的时候，\(H(X,Y)\) 剩下的信息量就是条件熵：\(H(Y|X)=H(X,Y)−H(X)\)

因此，可以这样理解，描述 X 和 Y 所需的信息是描述 X 自己所需的信息,加上给定 X 的条件下具体化 Y 所需的额外信息。

用一句话概括这一节：信息的作用在于消除不确定性，自然语言处理的大量问题就是寻找相关的信息。

3.互信息

在上一节中提到，当获取的信息和要研究的事物“有关系”时，这些信息才能帮助我们消除不确定性。如何量化地度量“相关性”，香农在信息论中提出了一个“互信息”（Mutual Information）的概念作为两个随机事件“相关性”的量化度量。

【互信息的定义】假定有两个随机事件 \(X\) 和 \(Y\)，它们的互信息定义如下：

\[I(X;Y)=\sum_{x\in X,y\in Y}P(x,y)log\frac{P(x,y)}{P(x)P(y)} \]

这个互信息就是上节介绍的随机事件 \(X\) 的不确定性（熵 \(H(X)\)），以及在知道随机事件 \(Y\) 的条件下的不确定性（条件熵 \(H(X|Y)\)）之间的差异，即

\[I(X;Y)=H(X)-H(X|Y) \]

即决策树中的信息增益

所谓两个事件相关的量化度量，就是在了解了其中一个 \(Y\) 的前提下，对消除另一个 \(X\) 的不确定性所提供的信息量。

互信息是一个取值在 \(0\) 到 \(min(H(X),H(Y))\) 之间的函数，

• 当 \(X\) 和 \(Y\) 完全相关时，互信息的取值是 \(H(X)\)，同时 \(H(X)=H(Y)\)；
• 当二者完全无关时，互信息的取值是0。

即互信息越大，两个随机事件越相关。（越相关，越能消除另一个事件的不确定性）。

在自然语言处理中，两个随机事件，或者语言特征的互信息是很容易计算的。只要有足够的语料，就不难估计出互信息公式中的 \(P(X,Y),P(X)\) 和 \(P(Y)\) 三个概率，进而算出互信息。因此，互信息被广泛用于度量一些语言现象的相关性。

机器翻译中，最难的两个问题之一是词义的二义性（又称歧义性，Ambiguation）问题。比如 Bush 可以是美国总统布什的名字，也可以是灌木丛。那么如何正确地翻译这些词呢？

法一：用语法，分析语句，等等。-> 迄今为止没有一种语法能很好地解决这个问题，Bush不论翻译成人名还是灌木丛，都是名词，在语法上没有太大问题。

法二：加规则“总统做宾语时，主语得是一个人”。-> 要是这样，语法规则就多得数不清，而且还有许多例外。

真正简单却非常实用的方法是使用互信息：

首先从大量文本中找出和总统布什一起出现的互信息量最大的一些词，比如总统、美国、国会、华盛顿，等等。再用同样的方法找出和灌木丛一起出现的互信息量最大的词，比如土壤、植物、野生，等等。有了这两组词，再翻译 Bush 时，看看上下文中哪类相关的词多就可以了。

这种方法最初由吉尔（William Gale），丘奇（Kenneth Church）和雅让斯基（David Yarowsky）提出。

4.相对熵（KL散度）

“相对熵”，在英语中是 \(Kullback-Leibler Divergence\)（KL散度）。

相对熵也用来衡量相关性，但和变量的互信息的不同，它用来衡量两个取值为正数的函数的相似性。

【相对熵的定义】设p(x), q(x)是离散型随机变量X的两个概率分布，p对q的相对熵是：

\[D_{KL}(p||q)=\sum_{x\in X} p(x)log\frac{p(x)}{q(x)} \quad\quad(4.1) \]

结论：

1. 对于两个完全相同的函数，它们的相对熵等于零。
2. 相对熵越大，两个函数的差异越大；反之，相对熵越小，两个函数的差异越小。
3. 对于概率分布或概率密度函数，如果取值均大于零，相对熵可以度量两个随机分布的差异性。
4. \(D_{KL}(p||q)>=0\)

小结：相对熵可以用来衡量两个概率分布之间的差异。
如果对于同一个随机变量 \(X\) 有两个单独的概率分布 \(p(x)\) 和 \(q(x)\)，我们可以使用KL散度来衡量这两个分布的差异。

维基百科对相对熵的定义：

In the context of machine learning, DKL(P||Q) is often called the information gain achieved if P is used instead of Q.
使用P来描述目标问题而不是Q，得到的信息增量。

例如，用P来表示样本的真实分布，Q表示模型所预测的分布，那么相对熵可以衡量Q还需要多少信息增量才能达到和P一样完美的描述。

相对熵是不对称的，即

\[D_{KL}(p||q) \neq D_{KL}(q||p) \]

这样使用起来有时不是很方便，为了让它对称，詹森和香农提出一种新的相对熵的计算方法，将上面的不等式两边取平均，即

\[D_{JS}(p||q)=\frac{1}{2}[D_{KL}(p||q)+D_{KL}(q||q)] \]

相对熵最早是用在信号处理上。如果两个随机信号，它们的相对熵越小，说明这两个信号越接近，否则信号的差异越大。后来研究信息处理的学者们也用它来衡量两段信息的相似程度，比如说如果一篇文章是照抄或者改写另一篇，那么这两篇文章中词频分布的相对熵就非常小，接近于零。在Google自动问答系统中，我们采用了上面的詹森-香农度量来衡量两个答案的相似性。

相对熵在自然语言处理中还有很多应用，比如用来衡量两个常用词（在语法和语义上）在不同文本中的概率分布，看它们是否同义。另外，利用相对熵，还可以得到信息检索中最重要的一个概念：词频率-逆向文档频率（TF-IDF）。

5. 交叉熵（cross entropy）

5.1 交叉熵的定义

对交叉熵的公式(4.1)变形可得到，

\[\begin{align*} D_{KL}(p||q)&=\sum_{x\in X}p(x)logp(x)-\sum_{x\in X}p(x)logq(x)\\ &=-H(p)+[-\sum_{x\in X}p(x)logq(x)] \end{align*} \]

等式的前一部分恰巧就是p的熵，等式的后一部分，就是交叉熵。

【交叉熵的定义】

\[H(p,q)=-\sum_{x\in X}p(x)logq(x) \]

所以有，\(D_{KL}(p||q)=H(p,q)-H(p)\).

在机器学习中，我们需要评估 label 和 prediction 之间的差距，可使用KL散度来度量，即 \(D_{KL}(y||\hat y)\)，而由于KL散度的前一部分 \(-H(y)\) 是一个常量（训练数据的分布是固定的），最小化KL散度等价于最小化交叉熵。

小结：交叉熵可以用来计算学习模型分布与训练分布之间的差异。交叉熵在逻辑回归的Sigmoid和Softmax函数中作为损失函数被广泛使用。

5.2 交叉熵在机器学习中的应用

在监督式机器学习中，无论是回归问题还是分类问题，都少不了使用损失函数（Loss Function）。损失函数是用来估量模型的预测值 f(x) 与真实值 y 的不一致程度。若损失函数很小，表明机器学习模型与数据真实分布很接近，则模型表现良好；若损失函数很大，表明机器学习模型与数据真实分布差别较大，则模型表现不佳。训练模型的主要任务就是使用优化方法来寻找损失函数最小时所对应的模型参数。

在线性回归中，常常使用 MSE(Mean Squared Error) 作为损失函数

\[loss = \frac{1}{2n}\sum_{i=1}^n(y_i-\hat{y_i})^2 \]

其中n代表样本个数。
MSE在线性回归问题中比较好用，而在分类问题中最常用的是交叉熵损失函数。

5.2.1 交叉熵在单标签场景下的使用

此处单标签指每一个样本只能有一个类别归属，例如一个图像样本，只能是猫或只能是狗。
定义损失函数：

\[loss = -\sum_{i=1}^my_ilog(\hat{y_i}) \]

上式为一个样本的损失计算方法，其中，m代表m种类别。
对于二分类问题，单个样本的损失计算可以简化为：

\[loss = -ylog(\hat y) -(1-y)log(1-\hat y) \]

例如，有如下样本：

对应的标签和预测值为：

	猫	青蛙	老鼠
label	0	1	0
prediction	0.3	0.6	0.1

那么，

\[loss = -[0*log(0.3)+1*log(0.6)+0*log(0.1)]=-log(0.6)=0.737 \]

对应一个batch的loss就是：

\[loss=-\frac{1}{n}\sum_{i=1}^n\sum_{j=1}^m y_{ij}log(\hat{y_{ij}}) \]

其中 n 为当前batch的样本数，m 为类别数。

5.2.2 交叉熵在多标签场景下的应用

此处多标签指一个样本可能有多个类别归属，例如一个图像样本，可能同时包含一只猫和一只狗。
例如，有如下样本：

对应的标签和预测值：

	猫	青蛙	老鼠
label	0	1	1
prediction	0.1	0.7	0.8

这里的prediction不再是通过softmax计算的了，而是采用sigmoid, 将每一个节点的输出归一化到[0,1]之间。所有 predictions 的值加起来不一定等于1。每一个label都是独立分布的，相互之间没有影响。所以交叉熵在这里是单独对每一个节点进行计算：

\[loss_猫=-0*log(0.1)-1*log(0.9)=-log(0.9)=0.152\\ loss_蛙=-1*log(0.7)-0*log(0.3)=-log(0.7)=0.515\\ loss_鼠=-1*log(0.8)-0*log(0.2)=-log(0.8)=0.322 \]

单个样本的 loss 即为 \(loss=loss_猫+loss_蛙+loss_鼠\)。
每一个batch的loss就是：

\[loss=\sum_{i=1}^n\sum_{j=1}^m [-y_{ij}log(\hat y_{ij})-(1-y_{ij})log(1-\hat y_{ij})] \]

其中 n 为当前batch的样本数，m 为类别数。

6. 补充

6.1 对数似然函数与交叉熵

逻辑回归中：log-likelihood等价于negative cross entropy，最大化log-likelihood等价于最小化cross entropy\(\rightarrow\)损失函数.
推导过程如下：
从极大似然的角度出发，预测类别的概率可以写成：

\[P(y|x)=\hat y^y\cdot (1-\hat y)^{(1-y)} \]

其中 \(y\) 代表真实的标签值，取值为1或0，\(\hat y\) 为预测概率值。
取log，可得到：

\[\begin{align*} logP(y|x)&=log(\hat y^y\cdot (1-\hat y)^{(1-y)})\\ &=ylog(\hat y)+(1-y)log(1-\hat y) \end{align*} \]

可见，对数似然函数等价于负交叉熵，于是最大化对数似然函数等价于最小化交叉熵。

6.2 softmax与交叉熵

一句话概括：softmax把模型的原始输出标准化成概率分布；cross entropy 刻画预测分类和真实结果之间的相似度。
多分类问题变为二分类问题时，softmax公式就转化为sigmoid公式，损失函数由cross entropy转化为binary cross entropy的形式。

6.3 关于softmax

softmax把分类预测的输出标准化，得到某个样本点归属于各个类别的概率分布。例如，归属于类别 \(j\) 的概率为：

\[p_j=softmax(z_j)=\frac{e^{z_j}}{\sum_{k=1}^K e^{z_k}} \]

其中 \(K\) 为类别数，\((z_1, z_2,..., z_K)\) 为模型的原始输出。
（对比 sigmoid 函数：\(sigmoid(x)=\frac{1}{1+e^{-x}}\) ）
这个结果满足了概率分布的标准化要求：在所有类别上的输出概率都不小于0，且所有类别上的输出概率和等于1。