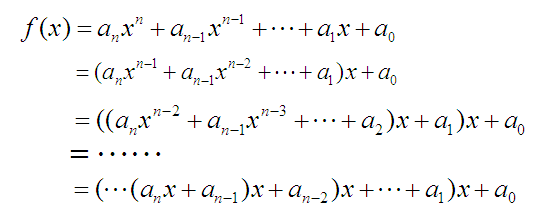算法 秦九韶算法
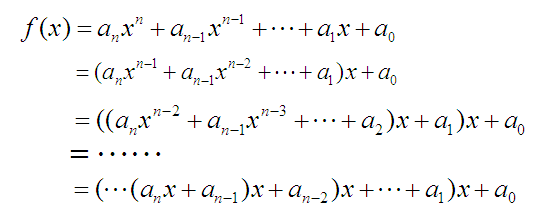
介绍
秦九韶算法又叫霍纳算法。 一般地,一元n次多项式的求值需要经过[n(n+1)]/2次乘法和n次加法,而秦九韶算法只需要n次乘法和n次加法。在人工计算时,一次大大简化了运算过程。
Pn(x)= anx ^n+a(n-1)x^(n-1)+…+a1x+a0
可简化成
Pn(x)= anx ^n+a(n-1)x^(n-1)+…+a1x+a0=((…(((anx +an-1)x+an-2)x+ an-3)…)x+a1)x+a0
java实现
1 package com.qyf404.learn.algorithm; 2 3 import java.math.BigDecimal; 4 5 /** 6 * 7 秦九韶算法又称霍纳算法。 一般地,一元n次多项式的求值需要经过[n(n+1)]/2次乘法和n次加法, 8 * 而秦九韶算法只需要n次乘法和n次加法。在人工计算时,一次大大简化了运算过程。 9 * 10 * Pn(x)= anx ^n+a(n-1)x^(n-1)+…+a1x+a0 11 * 12 * 可简化成 13 * 14 * Pn(x)= anx ^n+a(n-1)x^(n-1)+…+a1x+a0=((…(((anx +an-1)x+an-2)x+ 15 * an-3)…)x+a1)x+a0 16 * 17 * @author qyfmac 18 */ 19 public class HornerAlgorithm { 20 private double a[]; 21 private Double x; 22 23 public HornerAlgorithm(double[] a, double x) { 24 this.a = a; 25 this.x = x; 26 } 27 public void check(){ 28 if(a == null || x == null || a.length < 1 ){ 29 throw new RuntimeException(); 30 } 31 } 32 33 /** 34 * 简单的for循环实现 35 * 36 * 测试比较使用 37 * @return 38 */ 39 private double oldCompute() { 40 check(); 41 double s = 0; 42 for (int i = 0; i < a.length; i++) { 43 s = s + Math.pow(x, i) * a[i]; 44 } 45 return s; 46 } 47 /** 48 * 简单的for循环实现 49 * 50 * 测试比较使用 51 * @return 52 */ 53 private BigDecimal oldCompute2BigDecimal() { 54 check(); 55 BigDecimal x = new BigDecimal(this.x); 56 BigDecimal s = new BigDecimal(0); 57 for (int i = 0; i < a.length; i++) { 58 s = s.add(x.pow(i).multiply(new BigDecimal(a[i]))); 59 } 60 return s; 61 } 62 63 64 /** 65 * 秦九韶算法实现 66 * 67 * @return 68 */ 69 public double compute() { 70 check(); 71 72 int n = a.length -1; 73 double s = a[n]; 74 75 if(n == 0){ 76 //f(x)=a0 的情况 77 return s; 78 } 79 80 int i = 0; 81 do{ 82 i++; 83 s = a[n-i] + x * s; 84 85 }while(i < n); 86 87 88 return s; 89 } 90 /** 91 * 秦九韶算法实现 92 * 93 * @return 94 */ 95 public BigDecimal compute2BigDecimal() { 96 check(); 97 98 int n = a.length -1; 99 BigDecimal s = new BigDecimal(a[n]); 100 101 if(n == 0){ 102 //f(x)=a0 的情况 103 return s; 104 } 105 BigDecimal x = new BigDecimal(this.x); 106 int i = 0; 107 do{ 108 i++; 109 s = new BigDecimal(a[n-i]).add(s.multiply(x)); 110 111 }while(i < n); 112 113 114 return s; 115 } 116 117 public static void main(String[] args) { 118 // double a[] ={1}; 119 // double a[] ={1,1}; 120 // double a[] ={1,1,1}; 121 // double a[] ={1,1,1,2}; 122 double a[] = { 1 ,111.3 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,111 ,11}; 123 double x = 2; 124 HornerAlgorithm ha = new HornerAlgorithm(a, x); 125 126 { 127 long start = System.currentTimeMillis(); 128 BigDecimal s = ha.oldCompute2BigDecimal(); 129 long end = System.currentTimeMillis(); 130 System.out.println("耗时" + (end - start) + "结果为" + s); 131 } 132 { 133 long start = System.currentTimeMillis(); 134 BigDecimal s = ha.compute2BigDecimal(); 135 long end = System.currentTimeMillis(); 136 System.out.println("耗时" + (end - start) + "结果为" + s); 137 } 138 139 } 140 }
最终测试结果
1 耗时22结果为1139953162956611208548808572713851989272522501907096190014794725752241296178091297082821351384513148463092452900820004233019437006863981436491416946700513548219890381356958359367906614177967433056035.5999999999999943156581139191985130310058593750 2 耗时3结果为1139953162956611208548808572713851989272522501907096190014794725752241296178091297082821351384513148463092452900820004233019437006863981436491416946700513548219890381356958359367906614177967433056035.5999999999999943156581139191985130310058593750
结论
在n很大的时候,常规for循环时间复杂度O(n^2),而秦九韶算法时间复杂度O(2n)。