动态规划 - 归类总结
动态规划(DP)思想
动态规划 Dynamic programming => DP
动态规划:普通递归 + dp数组记录,达到空间换时间
动态规划一般都不会很高效,因为dp[]记录了途中每个状态最优解
尽量找巧妙的方法,来做到比dp效果更好的解法
DP三大性质:
- 最优子结构
- 子问题重叠
- 无后效性(算好的dp[]不会再改)
DP四步走:
- 拆分出子问题
- 子问题的递推公式(状态转移方程)
- 确定 DP 数组的计算顺序、并初始化
- 空间优化(可选)
动态规划vs贪心算法
贪心算法是一种特殊的动态规划算法
对于一个动态规划问题,问题的最优解往往包含重复的子问题的最优解,动态规划就是为了消除重复的子问题
而贪心算法由于每一次都贪心选取一个子问题,所以不会重复计算子问题的最优解
DP问题大致分类
- 【斐波拉切】(跳台阶系列)
- 【递推型】(丑数、剪绳子、圆圈最后数)
- 【划分型】间断序列-最值(打家劫舍、股票类、不连续子序列)
- 【二维坐标型】细分为:1)棋盘dfs回溯问题(flag试错) 2)棋盘dp[][]递推问题
- 【区间型】连续序列-最值(拿石子、连续子序列)=》二维dp[][],双指针
- 【背包型】目标值(背包(sum<=k)、和为K的序列(未必连续)、零钱兑换)
- 【树型】(树状递归、dp;经常划到树而不是动态规划)
前三类是一维dp[],紧接后面两类是二维dp[][],背包型可能1维、2维、多维
斐波拉切型
1. 斐波那契数列
大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0,第1项是1)。n≤39
public class Solution {
public int Fibonacci(int n) {
int[] fi=new int[40];//设置数组记录中间结果,不然重复计算太多 //根据题目,放心设置数组大小
fi[0]=0;fi[1]=1;
for(int i=2;i<=n;i++){
fi[i]=fi[i-1]+fi[i-2];
}
return fi[n];
}
}
//动态规划,时间复杂度O(N),空间复杂度O(N)
//如果用递归,时间复杂度O(1.618^N)【上网查的,略小于2^N】,空间复杂度O(1)【不包括系统栈空间】
2. 跳台阶
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果)。
1)斐波拉切-O(N)动态规划
public class Solution {
public int JumpFloor(int target) {
int frog[]=new int[100];
frog[1]=1;frog[2]=2;
for (int i=3;i<=target;i++){
frog[i]=frog[i-1]+frog[i-2];
}
return frog[target];
}
}
//原理同:斐波那契数列
//【动态规划】时间O(N),空间O(N)
//如果只要最后的结果,那么可以撤销数组,使用a/b/c三个变量存储即可。空间复杂度减为O(1)
2)空间O(1)的方法
public class Solution {
public int jumpFloor(int target) {
if(target<=2)return target;
int lastOne = 2; //现在位置上一个,相当于fi[i-1]
int lastTwo = 1; //相当于fi[i-2]
int res = 0;
for(int i=3; i<=target; ++i){
res = lastOne + lastTwo;
lastTwo = lastOne;
lastOne = res;
}
return res;
}
}
//这种方法的空间复杂度为:O(1)
//时间复杂度虽然也为O(N),但是比上一种动态规划的方法耗时,因为循环里面操作较多
//相当于时间换空间,花费时间在不断倒腾地方
3. 跳台阶扩展问题
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
1)找出公式
public class Solution {
public int JumpFloorII(int target) {
int way=1;for(int i=1;i<target;i++)way*=2;return way;
}
}
//【找出数学公式】2的n-1次方:类似向n个点之间的n-1个空画横线
// 其实不难找,在找递推公式时,前几项一写就知道了
// 时间 O(N)
// 空间 O(1)
2)(动态规划)硬算
public class Solution {
public int jumpFloorII(int target) {
int[] array =new int[100];
array[1] = 1;
for(int i=2; i<=target; ++i){
int sum = 0;
for(int j=1; j<=i-1; ++j)sum+=array[j];
array[i] = sum +1; //之前所有路径,再加上直接全部的1个跳法
}
return array[target];
}
}
//时间 O(N^2)
//空间 O(N)
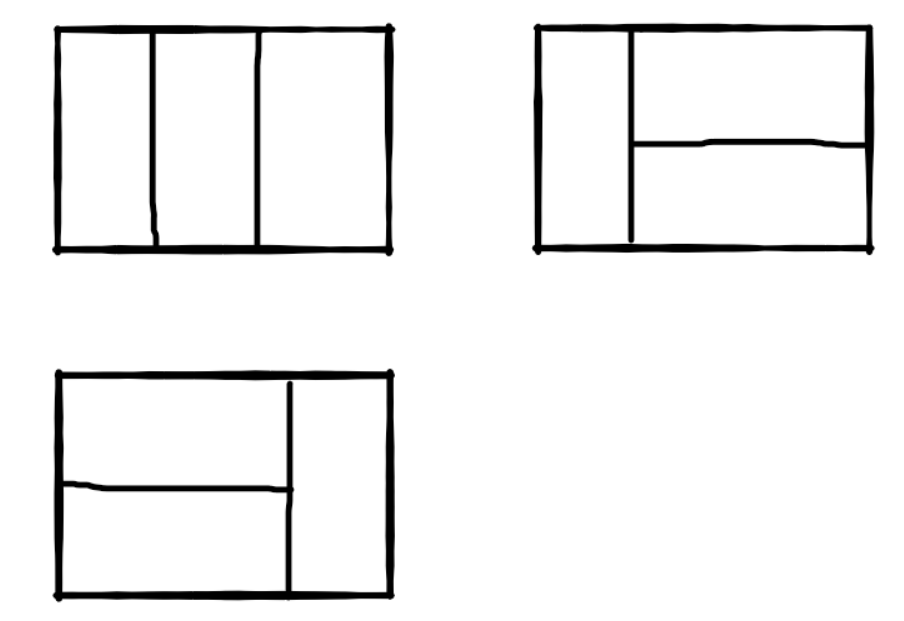
4. 矩形覆盖
我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2n的大矩形,总共有多少种方法?
比如n=3时,23的矩形块有3种覆盖方法:
public class Solution {
public int rectCover(int target) {
int fi[] = new int[100];
for(int i= 0; i<=2; ++i)fi[i]=i;
for(int i=3; i<=target; ++i)fi[i]=fi[i-1]+fi[i-2];
return fi[target];
}
}
//(除了初始少许不一样,后面是斐波拉切)
// 找递推关系:分解情况==》最右边只可能为竖或横两种情况,这两种情况无交集,分别占用1个块块和2个块块
递推型
1. 丑数
把只包含质因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,但14不是,因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。
import java.lang.Math;
public class Solution {
public int GetUglyNumber_Solution(int index) {
int ugly [] = new int [2000];
ugly[1] = 1;//第一个丑数是1 //ugly[]数组:从1开始,而不是0,增加可读性
int t2 = 1;
int t3 = 1;
int t5 = 1;//标记2/3/5这三个赛道中(非独立),潜在候选者的位置 //ugly[]下标 //t2t3t5跑得比i要慢
for(int i=2; i<=index; ++i){
ugly[i] = Math.min(Math.min(2*ugly[t2],3*ugly[t3]),5*ugly[t5]);//Java里面的min()太low了,只能两个数
if(ugly[i] == 2*ugly[t2]) ++t2;//t2沿着主干线ugly[]走到下一个:因为这个被选中了,选下一个为候选
if(ugly[i] == 3*ugly[t3]) ++t3;
if(ugly[i] == 5*ugly[t5]) ++t5;//为什么要搞三个类似语句?因为:这三个可能中一个、也可能中两个、或三个全中(三个因子都含有)
}
return ugly[index];
}
}
//时间 O(N) 空间 O(N)
2. 剪绳子
给你一根长度为n的绳子,请把绳子剪成整数长的m段(m、n都是整数,n>1并且m>1),每段绳子的长度记为k[0],k[1],...,k[m]。请问k[0]xk[1]x...xk[m]可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。(2 <= n <= 60)
方法一:数学函数求导法
【总体思路】构造函数求导,得到:m=n/e (小数的情况下),也就是说尽量拆成一堆:2、3(最接近e的整数)
数学函数求导法:针对性规律
result= f(m) = (n/m) ^m,设n为定值,m为自变量,f(m)为乘积结果。
max{ f(m) }= max{ ln f(m) },取对数。
求 ln f(m)= m*( ln n- ln m )最值点的m值,求导并令f(m)'=0,得到m=n/e.
e=2.718,然后因为取整数,所以是拆成一堆2、3;
具体看下:4>>>2x2;5>>>2x3;6>>>3x3 符合分析的结果。
public class Solution {
public int cutRope(int target) {
if(target == 2)return 1;//因为题目要求最少拆成2份
if(target == 3)return 2;
int res = 1;
while(target > 4 ){//target剩<=4时,三种情况:4=>2*2=4; 3=>3; 2=>2; (-=3 不存在1)
target -= 3;
res *= 3;
}
return res * target;//三种情况合并处理
}
}//时间O(N),空间O(1)
方法二:动态规划
【总体思路】dp[] 存一步步的最优 + 找到 递推公式
public class Solution {
int[] dp = new int[60];
public int cutRope(int target) {
if(target == 2) return 1;
if(target == 3) return 2;//这里的策略不同,要单独拎出来
dp[2] = 2;
dp[3] = 3;//在target>=4的前提下,dp[]数组2~3对应的值(不必强制分两段)
for(int i=4; i<=target; ++i){
int max = Integer.MIN_VALUE;
for(int j=2; j<=i-1; ++j){//果然,dp的本质是穷举
if(max < dp[j]*(i-j)) max = dp[j]*(i-j);//动态规划重点是找到=>【最优子结构的递推公式】
}//另一种递推:将上一行的(i-j)换成dp[i-j]
dp[i] = max;
}
return dp[target];
}
}//时间O(N^2) 空间O(N)
3. 孩子们的游戏(圆圈中最后剩下的数)
每年六一儿童节,牛客都会准备一些小礼物去看望孤儿院的小朋友,今年亦是如此。HF作为牛客的资深元老,自然也准备了一些小游戏。其中,有个游戏是这样的:首先,让小朋友们围成一个大圈。然后,他随机指定一个数m,让编号为0的小朋友开始报数。每次喊到m-1的那个小朋友要出列唱首歌,然后可以在礼品箱中任意的挑选礼物,并且不再回到圈中,从他的下一个小朋友开始,继续0...m-1报数....这样下去....直到剩下最后一个小朋友,可以不用表演,并且拿到牛客名贵的“名侦探柯南”典藏版(名额有限哦!!_)。请你试着想下,哪个小朋友会得到这份礼品呢?(注:小朋友的编号是从0到n-1;报数0到m-1)
如果没有小朋友,请返回-1
方法一:朴素模拟法 O(m*n)
public class Solution {
public int LastRemaining_Solution(int n, int m) {
if(n<=0 || m<=0)return -1;
ListNode head = new ListNode(0);
ListNode p = head;
for(int i=1; i<=n-1; ++i){
ListNode node = new ListNode(i);//串成链
p.next = node;
p = p.next;
}
p.next = head;//p回到开头位置的前一个,形成闭环
//还有一个作用是,让p指向head前一个开始,可以使每轮循环一样套路
for(int i=1; i<=n-1; ++i){
for(int j=1; j<=m-1; ++j){
p=p.next;
}
p.next = p.next.next;//java会自动回收,所以不管那个被删除的节点
}
return p.val;//剩下的最后一个
}
}//这种思路是:模拟完整的游戏运行机制,不跳步
//时间O(m*n) 空间O(n)
方法二:数学归纳法 O(n) [分析是难点]
public class Solution {
public int LastRemaining_Solution(int n, int m) {//时光倒流递推法:为什么要逆向?因为逆向是由少到多不会有空位;而正向会有空位,必须模拟、不能跳步
if(n<=0)return -1;
int res = 0; //f(1,m)=0
for(int i=2; i<=n; i++){//i就是小朋友数量,i=2是游戏最后一轮,但是我解法的第一轮 //循环从i=2到i=n,小朋友越来越多,此解法是倒推(时光倒流)
res = (res + m) % i; //相邻项关系:左边res是f(n,m) 右边res是f(n-1,m)
}
return res;
}
}//时间O(n) 空间O(1)
数学归纳法分析:
数学归纳法:
f(n,m)表示:【相对参考系:从0位置开始,最终到达f(n,m)位置】//例如:从0开始,最终到达f(5,3)=3的位置
f(1,m)=0;//首项
f(n,m)=[(m%n) + f(n-1,m)]%n;//公式化简为:f(n,m)=[m + f(n-1,m)]%n //相邻项关系【重点,推导如下】:
例如:
f(5,3)=[f(4,3)+ 3%5 ] %5=f(4,3)+3 什么意思?
f(5,3)从0开始,0-1-2,删除2节点,然后来到3==》这时的情况就类似f(4,3)。但还有一点不一样,就是标准的f(4,3)从0开始,而这里从3开始
f(4,3)根据定义,必须从0开始(所有的f(i,m)的定义需要一致),而不是从3。所以必须进行【对齐操作】:
于是f(5,3)的参靠系里:先走3步,然后以3为起点,走f(4,3)步 ==》f(5,3)=3+ f(4,3) [这里是简化,再考虑%n的细节优化下就ok了]
有了递推公式,用递归法or迭代法,求解都几乎同理
迭代法:f(1,m)=0 f(2,m)=[m + f(1,m)]%n ... 一直算到f(n,m)
划分型
1. 买卖股票的最佳时机 III
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
class Solution {
public int maxProfit(int[] prices) {
//本题的状态比较少,只有一维、而且只有4个状态
//这4个变量都是当前状态下的总profit:
int buy1 = prices[0];
int buy2 = prices[0];
int sell1 = 0;
int sell2 = 0;
for(int i=0; i<=prices.length-1; ++i){
//下面4行都是状态转移方程:
buy1 = Math.min(buy1, prices[i]);
sell1 = Math.max(sell1, prices[i]-buy1);
buy2 = Math.min(buy2, prices[i]-sell1);
sell2 = Math.max(sell2, prices[i]-buy2);
}
return sell2;
}
}//时间O(N) 空间O(1)
类似题目1
题目:只有一次买卖机会
解法:上面方法留下buy1和sell1即可
类似题目2
题目:k次买卖次数
解法:(难)上面方法加数组,加层循环
2. 买卖股票的最佳时机含手续费
每笔交易你只需要为支付一次手续费。
输入:prices = [1, 3, 2, 8, 4, 9], fee = 2
输出:8
class Solution {
public int maxProfit(int[] prices, int fee) {
int profit =0;
int buy = prices[0] + fee;
for(int i = 0; i<=prices.length-1; ++i){
if(buy > prices[i]+ fee)buy = prices[i]+ fee;//更新最低价
if(prices[i] > buy){
profit += (prices[i] - buy);
buy = prices[i];//这里是关键:当我们卖出一支股票时,我们就立即获得了以相同价格并且免除手续费买入一支股票的权利
}
}
return profit;
}
}//时间O(N) 空间O(1)
类似题目
题目:不限制买卖次数
解法:每步都操作,所有 "上坡" 都收下
3. 打家劫舍(不相邻最大子序列和)
给定一个代表每个房屋存放金额的非负整数数组,在不偷相邻两屋情况下 ,一夜之内能够偷窃到的最高金额。
关键点:
状态转移方程:dp[i] = dp[i-1] > dp[i-2]+nums[i-1] ? dp[i-1] : dp[i-2]+nums[i-1];
注意分析 dp[i]只需要和dp[i-1]、dp[i-2]的关系
class Solution {
public int rob(int[] nums) {
int len = nums.length;
int dp[] = new int[len + 1];//多一个
dp[0] = 0;
dp[1] = nums[0];
for(int i = 2; i<=len; ++i){
dp[i] = dp[i-1] > dp[i-2]+nums[i-1] ? dp[i-1] : dp[i-2]+nums[i-1];
}
return dp[len];
}
}//时间O(N) 空间O(N)
空间优化:
class Solution {
public int rob(int[] nums) {
int len = nums.length;
int two = 0;
int one = nums[0];
int zero = nums[0];
for(int i = 2; i<=len; ++i){
zero = one > two+nums[i-1] ? one : two+nums[i-1];//状态转移方程
two = one;
one = zero;
}
return zero;
}
}//时间O(N) 空间O(1)
//虽然这个时间也是O(N), 但是比上面的方法耗时(时间换空间)
4. 最长递增子序列
方法一:两重循环完全dp
描述:
一维数组dp[i]用于存储0-i序列的最大res,初始化为1
i、j 两重循环,当 nums[j] < nums[i] 时:
dp[i] = Math.max(dp[i], dp[j] + 1);
时间O(N^2) 空间O(N)
方法二:设置辅助数组
时间O(N*logN) 空间O(N)
import java.util.ArrayList;
class Solution {
public int lengthOfLIS(int[] nums) {
ArrayList<Integer> min = new ArrayList<Integer>();//这个tails未必是子序列的值,但长度一定是对的
min.add(nums[0]);
for(int num:nums){
int left = 0;
int right = min.size()-1;
if(num > min.get(right))
min.add(num);
else{
while(left < right){
int mid = (left+right)/2;
if(num <= min.get(mid)) right = mid;//这里while里面的写法挺多的,只要保证num与min[mid]相等时区间向左即可
else left = mid+1;
}
min.set(right,num);//left==right //每一轮必将最新数字插入队列
}
}
return min.size();
}
}
代码简短些的方法:
public class Solution {
public int LIS(int[] arr) {
int[] min = new int[arr.length];
int count = 0;
for(int num:arr){
int left = 0;
int right = count;//这里right包含min数组有效值的右边一个
while(left<right){
int mid = (left+right)/2;
if(num>min[mid])left = mid+1;
else right = mid;
}
if(count == right) ++count;
min[right]=num;
}
return count;
}
}
深化:要求输出最优序列(长度相同时,要求每个位置尽量小)
public class Solution {
public int[] LIS(int[] arr) {
int n = arr.length;
int[] min = new int[n];
int[] index = new int[n];//为每个arr元素,记录(min中的)更新下标
int count = 0;
for(int i=0; i<=n-1; ++i){
int left = 0;
int right = count;
while(left<right){
int mid = (left+right)/2;
if(arr[i]>min[mid])left = mid+1;
else right = mid;
}
if(count == right) ++count;
min[right]=arr[i];
index[i] = right;//记录(min[]中的)更新下标right
}
int[] res = new int[count];//
for(int i= n-1,k = count-1; i>=0; --i){//
if(k == index[i])res[k--]=arr[i];//一定要从右往左,才能拿到最新的
}
return res;
}
}
二维dp[][]递推型
1. 不同路径
方法一:动态规划
关键点:
1)状态转移方程:path[ i ][ j ] = path[ i-1 ][ j ] + path[ i ][ j-1 ];
2)初始化:第一行第一列初始化为1(因为都是只有一种方法)
class Solution {
public int uniquePaths(int m, int n) {
int[][] path = new int [m][n];
//由于最上的边、最左的边,初始化为1 (因为都是只有一种方法到达)
for(int i=0; i<=m-1; ++i)path[i][0]=1;
for(int j=0; j<=n-1; ++j)path[0][j]=1;
for(int i=1; i<=m-1; ++i){
for(int j=1; j<=n-1; ++j){
path[i][j]=path[i-1][j]+path[i][j-1];
}
}
return path[m-1][n-1];
}
}
时间 O(mn)、空间 O(mn)
方法二:组合数学
M x N 网格,从左上到右下
分析:一共(M-1)+(N-1)步,其中向右(M-1)步,所以是:
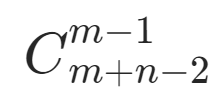
时间 O(n) 、空间O(1)
2. 最小路径和
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
public class Solution {
public int minPathSum(int[][] matrix) {
int row = matrix.length;
int col = matrix[0].length;
int[][]sum = new int[row][col];
int s = 0;
for(int i=0; i<=row-1; ++i){
s += matrix[i][0];
sum[i][0] = s;
}
s = 0;
for(int j=0; j<=col-1; ++j){
s += matrix[0][j];
sum[0][j] = s;
}
for(int i=1; i<=row-1; ++i){
for(int j=1; j<=col-1; ++j){
sum[i][j] = sum[i-1][j]<sum[i][j-1] ? sum[i-1][j]+matrix[i][j] : sum[i][j-1]+matrix[i][j];
}
}
return sum[row-1][col-1];
}
}//时间O(mn), 空间O(mn)
优化 Tips:
1)可以直接修改题目提供的grid数组,这样空间就是O(1)了。
2)如果使用sum[row+1][col+1]数组,虚拟的边上为0,就可以统一步骤、不用初始化的两个循环了。
类似题目
题目:三角形最小路径和
解法:
设置一个最小和的辅助dp数组
第1步:左边界、右边界只有一个"父";先把边计算好
第2步:里面的点来自两个"父"的min
第3步:取最下面一层的最小值
(空间优化:只保留计算的上一行即可)
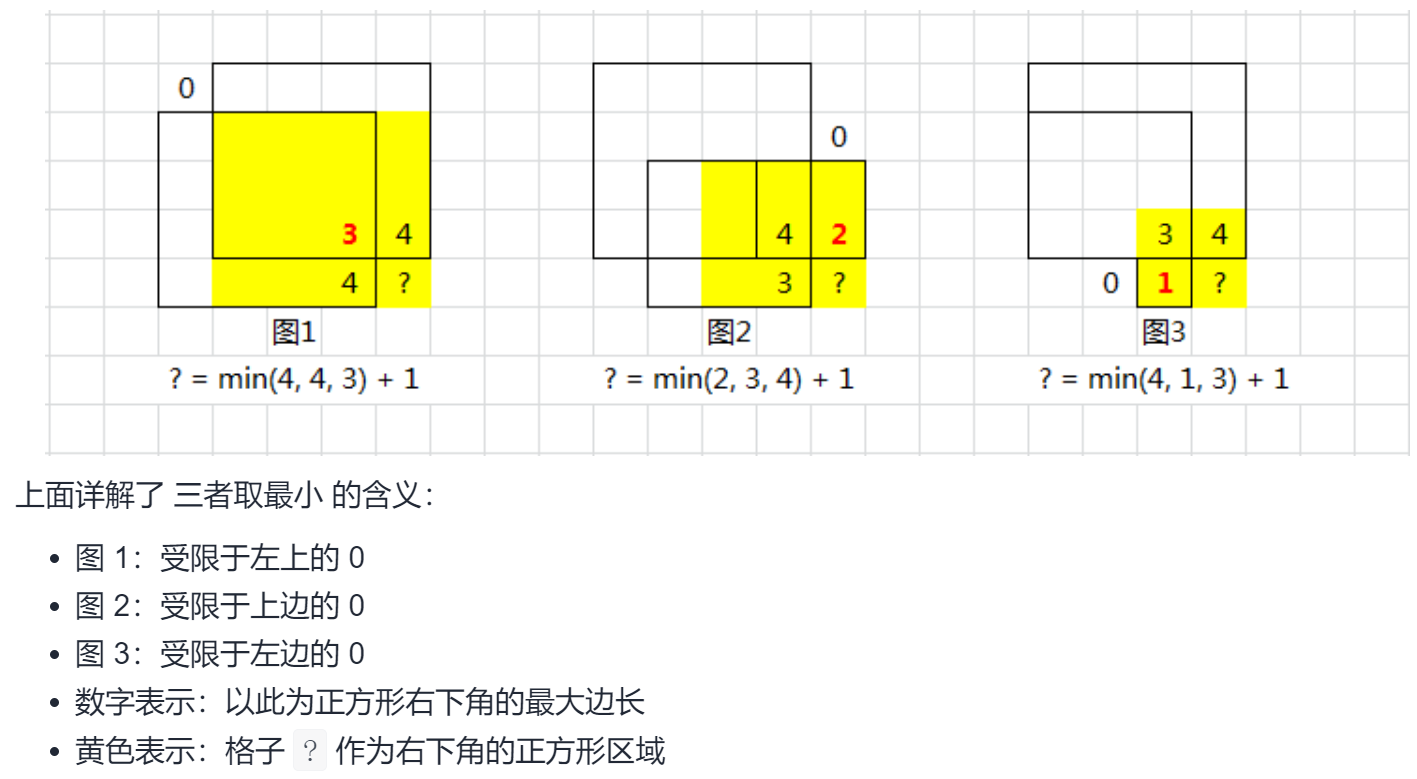
3. 最大正方形
二维棋盘上,所有值为 0或1。求全为1的最大正方形。
public class Solution {
public int maximalSquare(char[][] matrix) {//动态规划O(N^2) //暴力法O(N^4)
int maxSide = 0;
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return maxSide;
}
int rows = matrix.length;
int columns = matrix[0].length;
int[][] dp = new int[rows][columns];
for (int i = 0; i < rows; ++i) {
for (int j = 0; j < columns; ++j) {
if (matrix[i][j] == '1') {//右下角为非空
if (i == 0 || j == 0) {
dp[i][j] = 1;
} else {
dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;//这句是核心 //左、上、左上 3者之中最小的+1
}
maxSide = Math.max(maxSide, dp[i][j]);
}
}
}
int maxSquare = maxSide * maxSide;
return maxSquare;
}
}
二维dfs回溯型(flag试错)
1. 矩阵中的路径
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。如果一条路径经过了矩阵中的某一个格子,则该路径不能再进入该格子。例如:

矩阵中包含一条字符串"bcced"的路径,但是矩阵中不包含"abcb"路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入该格子。
【总体思路】(dfs+剪枝) x 多个起点
public class Solution {
public boolean hasPath (char[][] matrix, String word) {
boolean flag[][] = new boolean[matrix.length][matrix[0].length];//flag[][]数组,初始化为false,表示未经过的点
//一次初始化,之后共用 ==>是因为每次试探后,都会复原flag数组
for(int i = 0; i<= matrix.length-1; ++i){
for(int j=0; j<=matrix[0].length-1; ++j){//每行每列的全部格子作为起点,开始尝试
if(dfs(matrix, word, i, j, 0, flag)==true)return true;//如果找到一个,则完成任务+停止尝试,立即返回true
}
}
return false;//全部失败,返回false //单个尝试的失败不会有任何返回
}
public boolean dfs(char[][] matrix, String word, int i, int j, int count, boolean flag[][]){
if(0<=i && i<= matrix.length-1 && 0<=j && j<=matrix[0].length-1){//统一拦截==>【剪枝】
if(matrix[i][j] == word.charAt(count) && flag[i][j]==false){//匹配++
++count;//也可以在后面都用count+1
if(count == word.length())return true;//完整匹配,则主动停止 //全文仅此一处、是true的源头
flag[i][j] = true;//【尝试改flag】(与下文还原flag对应)
//下面递归结构类似4叉树的递归:
if(dfs(matrix, word, i+1, j, count, flag)
|| dfs(matrix, word, i-1, j, count, flag)
|| dfs(matrix, word, i, j+1, count, flag)
|| dfs(matrix, word, i, j-1, count, flag)
)return true;//这个return true是带有if的、起到传递true的作用,它不是源头
flag[i][j] = false;//【还原flag】//注意,平时传值都不需要"还原"(如count),而这里需要。
} //说明flag[][]数组,传的是指针(而不是提供副本),递归分支是共用一个的
}
return false;
}
}//时间:O(rows*cols*3^word)//3是因为不能回头、减少一种路
//空间:1)flag空间 O(rows*cols) 2)栈空间O(word)
//如果有类似线性匹配的KMP模式串的优化,会快一些
2. N皇后问题
牛客N皇后
两种方法都是基于动态规划(回溯):
方法一:二维数组+4个方向探索+起点只从第一行开始+设置二维flag表示是否可能新落子
方法二:一位数组(i、A[i]分别表示行、列)+单向探索
回溯的本质是" 科学地 穷举 "
本题时间复杂度O( N! )
3. 机器人的运动范围
地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于k的格子。 例如,当k为18时,机器人能够进入方格(35,37),因为3+5+3+7 = 18。但是,它不能进入方格(35,38),因为3+5+3+8 = 19。请问该机器人能够达到多少个格子?
【总体思路】dfs+剪枝
public class Solution {//相邻方格移动 //由于各个位相加(非线性)造成跳步困难,所以用相邻探索的方法
int count = 0;
public int movingCount(int threshold, int rows, int cols) {
boolean flag[][] = new boolean[rows][cols];//标记方格有没有来过,这里的flag不可逆
dfs(threshold, rows, cols, 0, 0, flag);//从(0,0)开始探索。。
return count;
}
public void dfs(int threshold, int rows, int cols, int i, int j, boolean flag[][]){
if(0<=i && i<=rows-1 && 0<=j && j<=cols-1){
if(flag[i][j] == false && i/10 + i%10 + j/10 + j%10 <= threshold){//i、j属于[0,99]
++count;
flag[i][j] = true;//不用还原
//如果一个块块不符合,它周围就不用再试了
dfs(threshold, rows, cols, i+1, j, flag);
dfs(threshold, rows, cols, i-1, j, flag);
dfs(threshold, rows, cols, i, j+1, flag);
dfs(threshold, rows, cols, i, j-1, flag);
}
}
}
}//时间O(rows*cols) 空间O(rows*cols)
//不能用两层for循环来做是因为:本题需要相连的空间,所以必须bfs、dfs二选一
//感觉修改一下就是迷宫找路
4. 海岛数量
给出二维矩阵,其中1是海岛、0是海。求一共有多少个海岛(1的连接区域)?
public class Solution {
static int count = 0;//黑区域数量(海岛数量)
public static void main(String[] args) {
int[][] bitmap = {{1, 0, 0}, {0, 0, 1}, {0, 0, 1}};
System.out.println("connectedComponts(bitmap) = " + connectedComponts(bitmap));
}
public static int connectedComponts (int[][] bitmap) {
//boolean black = false;
int rows = bitmap.length;
int cols = bitmap[0].length;
boolean flag[][] = new boolean[rows][cols];
for(int i=0; i<=rows-1; ++i){
for(int j=0; j<=cols-1; ++j){
dfs(i,j,rows,cols,flag,bitmap, false);//每次由1进去一次,就使总的黑区域+1
}
}
return count;
}
public static void dfs(int i, int j, int rows, int cols, boolean[][] flag, int[][] bitmap, boolean black){
if(0<=i && i<=rows-1 && 0<=j && j<=cols-1){//在区域内
if(flag[i][j] == false && bitmap[i][j]==1){
if(black == false){//这里是整个的核心!!!
count++;
}
flag[i][j] = true;//走过
dfs(i+1,j,rows,cols,flag,bitmap, true);
dfs(i-1,j,rows,cols,flag,bitmap, true);
dfs(i,j+1,rows,cols,flag,bitmap, true);
dfs(i,j-1,rows,cols,flag,bitmap, true);
}
}
}
}//时间复杂度是O(cols*rows),因为每个陆地最多走一遍,就会被flag标记,后面遇到直接跳出。
区间型
1. 最长回文子串
给定字符串A以及它的长度n,请返回最长回文子串的长度。
输入:"abc1234321ab",12
返回值:7
方法一:暴力求解(穷举)
i、j两重循环表示开始结束的坐标,然后O(N)判断是否对称
时间O(N^3)
空间O(1)
方法二:动态规划
dp [ i ] [ j ]存储:i开始、j结束的串
P(i,j) <-- P(i+1,j−1)
时间O(N^2)
空间O(N^2)
方法三:中心扩展法
从每个点开始,
同时向左右扩展、判断是否相等
时间O(N) x O(N) = O(N^2)
空间O(1)
public class Solution {
public int getLongestPalindrome(String A, int n) {
int maxLen = 0;
for(int i=0; i<=n-2; ++i){//i==n-1略过
int len1 = expand(A, i, i);//1)单中心
int len2 = expand(A, i, i+1);//2)双中心
int len = len1 > len2 ? len1 : len2;
if(len > maxLen) maxLen = len;
}
return maxLen;
}
public int expand(String A, int left, int right){
while(0<=left && right<=A.length()-1 && A.charAt(left)==A.charAt(right)){
--left;
++right;
}
return right-left-1;//right-left+1-2
}
}//时间O(N^2) 空间O(1)
方法四:Manacher 算法
时间O(N)
空间O(N)
算法较为复杂,后面再记一下
2. 石子游戏
A和B用几堆石子在做游戏。偶数堆石子排成一行,每堆都有正整数颗石子。
游戏以谁手中的石子最多来决出胜负。石子的总数是奇数,所以没有平局。
A和B轮流进行,A先开始。 每回合,玩家从行的开始或结束处取走整堆石头。 这种情况一直持续到没有更多的石子堆为止,此时手中石子最多的玩家获胜。
假设A和B都发挥出最佳水平,当A赢得比赛时返回 true ,当B赢得比赛时返回 false 。
方法一:动态规划
三角形阶梯dp数组,i,j分别是连续石子堆的左右边界,dp[i][j]表示领先石子数
初始化底层n个为石子堆数量,然后每次在边界增加一堆石子(左/右)
dp[i][j] = Math.max(piles[i] - dp[i + 1][j], piles[j] - dp[i][j - 1]);
res= dp[0][len-1]
时间O(N^2)
空间O(N^2)可优化为O(N)
方法二:直接 return true
==> 如果两人都是最佳策略,先手必胜
3. 连续子数组的最大和
输入一个整型数组,数组里有正数也有负数。数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。要求时间复杂度为 O(n).
//这是实用算法课上讲过的方法
public class Solution {
public int FindGreatestSumOfSubArray(int[] array) {
if(array.length ==0)return 0;
int max = Integer.MIN_VALUE;//全局最大值 //(这里将max=array[0]也可)
int currentSum = 0;//邻近最大值:小于0时候熔断,最小为0
for(int i =0; i<=array.length-1; ++i){
currentSum += array[i];
if(currentSum > max) max=currentSum;
if(currentSum<0)currentSum=0;
}
return max;
}
}
//时间 O(N) 空间 O(1)
4. 最大矩形(连续二维数组)
此类问题是上面连续子数组最大和的二维升级版,
核心思路是:转换压缩到一维问题,也就是将一竖排都压缩到一个值,用两重循环来遍历,分别确定上下界start/end
public class Main {
public int MaxMatrix(int[][]matrix) {
int rows = matrix.length;
int cols = matrix[0].length;
int res = Integer.MIN_VALUE;
for(int begin = 0; begin<=rows-1; ++begin){//上边界
int[] line = new int [cols];//每一列之和 //修改上边界之后,要清空重新开始
for(int end = begin; end<= rows-1; ++end){//下边界
//计算列元素和
for(int j=0; j<=cols-1; ++j){
line[j] += matrix[end][j];//下边界每向下一行,就计算更新下line[]数组的值
//上边界固定,下边界依次计算=>避免重复计算
}
res = Math.max(res,line[0]);
int sum = 0;
for(int j=0; j<=cols-1; ++j){
sum += line[j];
res = Math.max(res,sum);//取最大
if(sum<0)sum=0;//小于零,置零
}
}
}
return res;
}
}//这一题的思路是:由一维的连续子数组最大和,然后扩展到上下界的遍历,则可计算二维问题。
//时间复杂度O(N^3) //应该是最优解了
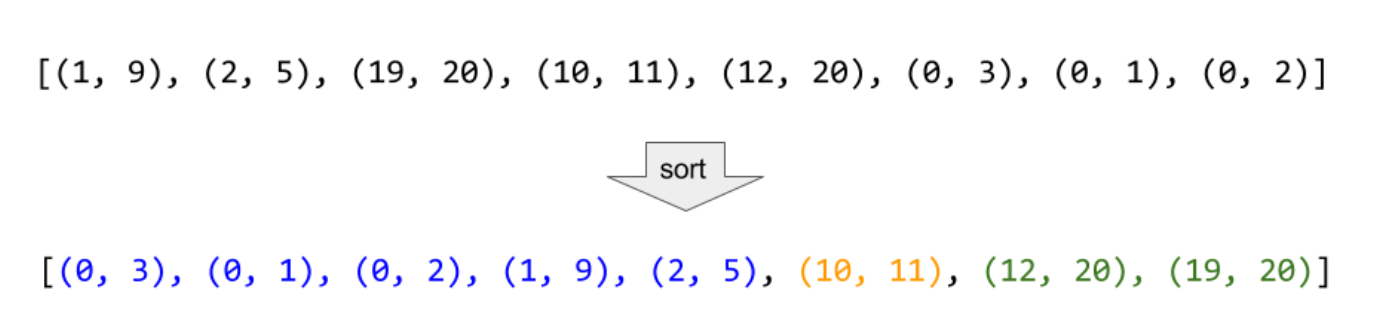
5. 合并区间
方法:按照区间左端点排序,然后向右遍历;
不断更新合并后区间的右端点,
如果遇到合并后右端点 小于 下一个的左端点,就重新开始一个区间;
时间复杂度O(N*logN):先排序、后线性遍历
6. 射箭问题
方法:按照区间右端点排序,然后向右遍历;
如果遇到右端点 小于 下一个的左端点,就换下一个右端点重开;
时间复杂度O(N*logN):先排序、后线性遍历
public class Solution {
// 贪心策略:先将左右区间按照右端点排序,然后从小到大扫描,
// 如果遇到右端点小于左端点,就换成此区间的右端点(并且count++),然后继续扫描
public int findMinArrowShots (int[][] targets) {//每个区间代表靶子的上下界,尽量多重射穿靶子
if(targets == null || targets.length==0) return 0;
Arrays.sort(targets, new MyComparator());
int res = 1;
int lastEnd = targets[0][1];
for(int i=1; i<targets.length; ++i){
if(targets[i][0] > lastEnd){
res++;
lastEnd = targets[i][1];
}
}
return res;
}
//特殊的比较方法,需要自己写:
//实现Comparator接口类,重写compare方法。
class MyComparator implements Comparator<int[]>{
public int compare(int[] X, int[] Y){
return X[1] - Y[1];
}
}
}
背包型
1. 分割等和子集【0-1背包问题】
==》问题等价于:不连续子集和为 k(本题k=sum/2)
和【0-1背包问题】不同的是:背包要 <= k,这里是==k
class Solution {
public boolean canPartition(int[] nums) {
int sum = 0;
for(int num : nums)sum += num;
if((sum & 1) == 1)return false;//位运算,看二进制最后一位是不是1
int target = sum/2;
boolean[] dp = new boolean[1+target];
dp[0] = true;
for(int i=0; i<=nums.length-1; ++i){//nums[i]
boolean[] mem = new boolean[1+target];//用于记录;空间优化方法是从后往前
for(int k=0; k<=target; ++k){//dp[k]
if(dp[k]==true) mem[k]=true;
}
for(int k=0; k<=target; ++k){
if(mem[k]==true && k + nums[i]<=target){
dp[k + nums[i]]=true;
}
}
}
return dp[target];
}
}
空间优化:
class Solution {
public boolean canPartition(int[] nums) {
int sum = 0;
for(int num : nums)sum += num;
if((sum & 1) == 1)return false;
int target = sum/2;
boolean[] dp = new boolean[1+target];
dp[0] = true;
for(int i=0; i<=nums.length-1; ++i){
for(int k=target; k>=0; --k){//dp[k]从后往前
if(k-nums[i]>=0 && dp[k-nums[i]]==true)dp[k]=true;//优化
}
}
return dp[target];
}
}//时间 O(len * target)
//空间 O(target)
2. 零钱兑换【完全背包问题】
- 【0/1背包问题】:每个元素最多选取一次
- 【完全背包问题】:每个元素可以重复选择
- 【分类背包问题】:有多个背包,分别装不同东西,需要多重遍历
class Solution {
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];//i和dp[i]分别为总金额、硬币数量
Arrays.fill(dp, Integer.MAX_VALUE-1);//
dp[0] = 0;//
for(int i=1; i<=amount; ++i){
for(int j=0; j<=coins.length-1; ++j){
if(i-coins[j]>=0 && dp[i-coins[j]]+1 < dp[i]){
dp[i] = dp[i-coins[j]]+1;
}
}
}
if(dp[amount]<=amount) return dp[amount];//这里判断含有等于
else return -1;//未找到方法,则dp[i]里面还是初始值
}
}//时间O(amount*coin) 空间O(amount)
3. 一和零【分类背包问题】
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的大小,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
int[][] dp = new int[m+1][n+1];//第一行第一列自动初始化为0
for(String str:strs){//
int zeros = 0;
int ones = 0;
for(char c:str.toCharArray()){//连续用两个高级for循环
if(c=='1')++ones;
else ++zeros;
}
for(int i=m; i>=0; --i){//背包内容在外层,dp在内层
for(int j=n; j>=0; --j){//背包经典的回退--
if(i-zeros>=0 && j-ones>=0 && dp[i][j] < dp[i-zeros][j-ones] + 1){//要求:1.无数组溢出 2.更优才更新
dp[i][j] = dp[i-zeros][j-ones] + 1;
}
}
}
}
return dp[m][n];
}
}
//时间复杂度 O(S*M*N), 其中S为strs[]元素个数
//空间复杂度 O(M*N)
本文先简要说明了动态规划的特点,然后给出问题的大致分类;
后面按照题目类型给出高频算法题的题解,以及详细的注释分析;
希望能对大家关于动态规划方面有一个overview的认识,并帮助大家刷题备考!




