支配树
背景
最近学到了一种新算法,但是很遗憾,在考试的时候,没能看出来。
于是决定写一篇博客来梳理一下。QAQ
【网上那么多题解,于是我就换一种讲法吧
没有太多的证明,更多的是自己的感性理解,如果有问题欢迎指出^-^
支配树的学习一定要循序渐进QAQ
问题
现在我们有一张有向图,求问当一个点 x 被删去的时候,有多少个点无法从起点到达?
换句话说,从起点到点 x 必须要经过哪些点?
显然,我们可以通过删边+BFS,O(nm)的完成这个问题。
有没有什么优秀的算法能够有效的降低复杂度呢?
支配树。
支配点的定义
学习什么是支配树的构造之前,先了解一下,什么是支配。
在一张 有向图 上面,如果点A被删除,那么B点就无法到达,那么称 A点是B点的支配点 。
很显然,对于每个点来说,有且至少有一个支配点,并且这些支配点之间呈现传递关系。【即 A支配B,B支配C,就有A支配C
支配点的选择范围
首先,我们需要一张有向图。

观察上图,就拿点7来举例子。
很明显,能够支配他的点就是1,4.
问题就出现了,1.4这两个点对于7点来说有什么特殊性质吗?
1. 放在一张有向图中来看,显然,他们是父子关系。
2. 对于一个DAG,1.4的拓扑序小于7点。
所以显然,我们可以通过一通乱搞,把每一个点的支配点集求出。【先别管怎么搞,假定已经会找了QAQ
那么我们就可以通过每个点向他的直系支配点【最近支配点 连边的方式构造出一颗树
就比如上面这张图构造成一颗树之后就是下图

这棵树就是支配树,从起点走向每一点所路过的所有点就是他的支配点。
支配树的构造
树形结构
对于一棵树来说,他本身就是自己的支配树。
DAG
DAG上的问题向来就是简单的多了,但是看出来是一个DAG可不太简单。【这我没办法,看不出来就打一般代码就完事
同样我们需要一个DAG来感受一下。
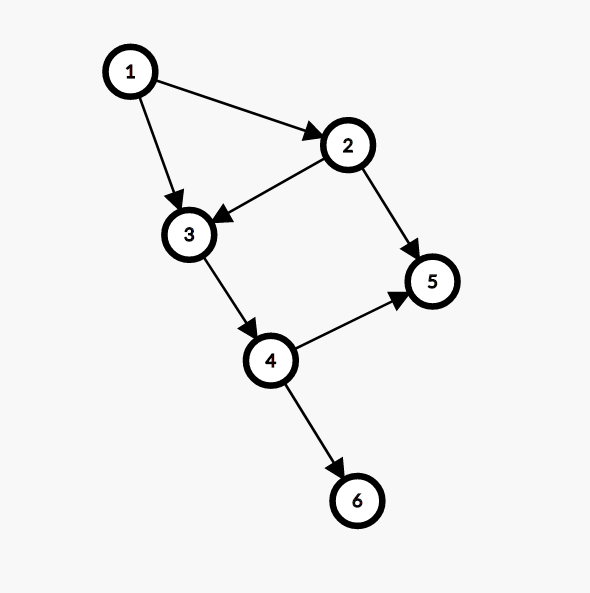
肉眼可见,点5的支配点集为{1}
试分析:
由于点5有两个入点2,4,所以2,4都不是支配点。
那么问题就转化成了,从起点1到达2和4的路径上面有哪个点是必经的?
先只考虑最近的支配点【其余的点可以从通过求支配点的支配点来得到
很容易就能想到,这个最近支配点就是点2,4的LCA。
那么接下来就进行不断地传递求出所有的支配点。
那么我们就可以得到一种求法
倍增求出能够到达这个点 x 的所有点的LCA,记为father,那么father就是x在支配树上面的父亲。
复杂度O(nlogn)
一般有向图
还记得支配点的定义吗?
删除x的支配点之后,就无法从起点走到x点。
先假想,这不是一个有向图,他的边是无向的,那么这个问题想必就简单多了。
很明显,这就是一个割点问题。
那么在有向图的情况下,tarjan能不能发挥一定的作用呢?
接下来我们就用dfn来尝试做一些操作。
首先,我们需要把一张图给扣出来一棵树【起点为根
如何选取树上的点呢?
我们学过一个东西,dfs树。
dfs树有一个很好的性质:
若图中两点x,y的 dfn[x] <= dfn[y],则任意从x到y的路径必然包含他们在dfs树中的一个公共祖先。
那么我们就可以选取这个dfs树作为我们选取的生成树。
接下来,进行一些定义【一定要记牢,不然之后会乱。
1. 半支配点 :
存在一个从点u到点v的路径中(不包括u,v),所有dfs树的点的dfn都大于dfn[v],并且如果u是v在dfs树上的父节点,那么u也是v的半支配点。【说白了就是支配点的选择范围。
不过如果要记录一个点所有的支配点会很困难。不过,既然支配点之间具有传递关系,那么我们就可以只记录最近的半支配点。
所以我们定义一个数组semi[ ]【Semi-domination 半支配 来记录最近的半支配点。
2.祖先
刚刚说了需要记录最近半支配点,然后通过传递的方式来还原出来整条传递关系。那么我们就需要记录一个数组来表示祖先。
所以我们定义一个数组anc[ ]【ancestry 祖先 来记录传递关系。
之前提到我们要通过dfn[ ]来做,并且提到了dfn值之间的大小关系,放到支配树上面,就是x的直系父亲【最近anc 需要满足:
semi[直系父亲] = semi[x]
这是建树很重要的一步,然而一次次的查找太浪费时间了,所以我们还需要定义一个数组。
定义数组min_anc[ ]表义为每个点的dfs树上面的semi[ ]值最小的祖先。
这样的话,我们就可以在找出的这个dfs树上面通过semi[ ]的传递关系,建出来这个新的支配树了。
一般图建立支配树的实现总结
上面并没有讲的很详细,很多证明都是感性理解的过去了。【不过也不太重要,理解意思就可以了。如果想要细致的理解的话,可以看这篇博客。
可能看到这里会有一些逻辑混乱【跟我的语文水平也有关系QAQ,那么我就再简单的总结一下。
首先,我们从一张图中扣出一棵具有良好性质的树。【dfs序的处理
然后,计算每个点的半支配点,这里再更细的说一下具体的实现吧:
1. 在点x的祖先链上面处理出来semi[ ]的最小值。
2. 通过带权并查集给根找到父亲。【通过semi[ ]的传递关系来构造,上面min_anc[ ]的定义时有写。
int fi_fa(int x) { if(x==anc[x]) return x; int father=anc[x]; anc[x]=fi_fa(anc[x]); if(dfn[semi[min_anc[x]]]>dfn[semi[min_anc[father]]]) min_anc[x]=min_anc[father]; return anc[x]; }
再者,通过半支配点来计算支配点。
最后,向直系支配点连边构造支配树。
时间复杂度
网上说这个算法的复杂度是 O(n α(n))
小结
支配树相关的内容到此就完结了,可能有很多的没说清楚的地方,欢迎能看到这里的你在评论区指出我的不足之处【如果没有看懂的话一定要提出自己的问题,我们一起完善这篇博客
最后,有什么不懂的写法,就看看我的代码吧【这是结合了我的理解和网上很多代码的产物,可能不是最短的,但是很清晰QAQ
代码的题面来自luogu的模板题

#include<iostream> #include<cstdio> #include<cmath> #include<cstring> #include<algorithm> #include<vector> #include<queue> using namespace std; const int maxn=3e5+7; int n,m; struct node{ int head[maxn],ecnt; struct ss{ int to,nxt; }tr[maxn<<1]; void add(int a,int b) { tr[++ecnt].nxt=head[a]; tr[ecnt].to=b; head[a]=ecnt; return; } }mp,un_mp,dfs_tr,undfs_tr,nw_tr;//原图,反图,dfs树,反dfs树,支配树 int cnt,dfn[maxn],id[maxn],fa[maxn]; void dfs(int x) {//寻找dfs树 id[dfn[x]=++cnt]=x; for(int i=mp.head[x];i;i=mp.tr[i].nxt) { int y=mp.tr[i].to; if(!dfn[y]) { dfs(y); fa[y]=x; dfs_tr.add(x,y); } } return; } int anc[maxn],min_anc[maxn],semi[maxn];//Semi-domination半支配 表示v点的所有半支配点的最小的那个 /**半支配点: 存在从一个点u到v的路径中(不包括u,v),所有dfs树的点的dfn都大于v的dfn 如果u是v在dfs树上的父节点,那么u也是v的半支配点 **/ 的semi最小的那个祖先,所以semi[mn[x]]=semi[x]; int fi_fa(int x) { if(x==anc[x]) return x; int father=anc[x]; anc[x]=fi_fa(anc[x]); if(dfn[semi[min_anc[x]]]>dfn[semi[min_anc[father]]]) min_anc[x]=min_anc[father]; return anc[x]; } void sp_tarjan() { for(int i=1;i<=n;i++) anc[i]=min_anc[i]=semi[i]=i; for(int j=n;j>1;j--) { int x=id[j]; if(!x) continue; int res=j; for(int i=un_mp.head[x];i;i=un_mp.tr[i].nxt) { int y=un_mp.tr[i].to; if(!dfn[y]) continue; if(dfn[y]<dfn[x]) res=min(res,dfn[y]); else { fi_fa(y); res=min(res,dfn[semi[min_anc[y]]]); } } semi[x]=id[res]; anc[x]=fa[x]; dfs_tr.add(semi[x],x); } return; } int in[maxn],dept[maxn],fath[maxn][30]; int lca(int x,int y) { if(dept[x]<dept[y]) swap(x,y); int d=dept[x]-dept[y]; for(int i=0;i<=20;i++) if((1<<i)&d) x=fath[x][i]; if(x==y) return x; for(int i=20;i>=0;i--) { if(fath[x][i]!=fath[y][i]) { x=fath[x][i]; y=fath[y][i]; } } return fath[x][0]; } void built_tree(int x) { int son=undfs_tr.tr[undfs_tr.head[x]].to; for(int i=undfs_tr.head[x];i;i=undfs_tr.tr[i].nxt) { int y=undfs_tr.tr[i].to; son=lca(son,y); } dept[x]=dept[son]+1; fath[x][0]=son; nw_tr.add(son,x); for(int i=1;i<=20;i++) fath[x][i]=fath[fath[x][i-1]][i-1]; return; } void topu() { for(int x=1;x<=n;x++) { for(int i=dfs_tr.head[x];i;i=dfs_tr.tr[i].nxt) { int y=dfs_tr.tr[i].to; in[y]++; undfs_tr.add(y,x); } } for(int i=1;i<=n;i++) { if(!in[i]) { undfs_tr.add(i,0); dfs_tr.add(0,i); } } queue<int> q; q.push(0); while(!q.empty()) { int x=q.front(); q.pop(); for(int i=dfs_tr.head[x];i;i=dfs_tr.tr[i].nxt) { int y=dfs_tr.tr[i].to; if(--in[y]<=0) { q.push(y); built_tree(y); } } } return; } int siz[maxn]; void re_dfs(int x) { siz[x]=1; for(int i=nw_tr.head[x];i;i=nw_tr.tr[i].nxt) { int y=nw_tr.tr[i].to; re_dfs(y); siz[x]+=siz[y]; } return; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { int x,y; scanf("%d%d",&x,&y); mp.add(x,y); un_mp.add(y,x); } dfs(1); sp_tarjan(); topu(); re_dfs(0); for(int i=1;i<=n;i++) cout<<siz[i]<<" "; cout<<endl; return 0; }
题目推荐
luogu模板题自然就不用说了
luogu灾难 【一个DAG的问题,很好的练手题
小强和阿米巴
谢谢!【完结撒花!


