数论总结之 乘法逆元

　　最近在补数论的知识，然后发现其实很多地方都要用到逆元。

　　所以我来了，写篇博客证明一下我其实是会的。【假的

　　参考自【洛谷日报第30期】。

乘法逆元

　　首先，假设你会扩展欧几里得（exgcd）的话，那么乘法逆元就很简单了。

　　首先看一下定义：

　　在(mod p) 意义下（ p 是素数），如果 a*a'=1 ，那么我们就说 a' 是 a 的逆元。当然啦，反过来， a 也是 a' 的逆元。

　　感觉跟倒数很像啊。

　　确实是这样没错，比如我们求组合数的时候，经常就会用到它，可以说是非常有用了。

　　逆元一般的表示方法是 inv，基本上看见这个变量，就都是逆元。

　　接下来我们来看看逆元都有什么性质，进一步了解一下逆元的应用。

　   一.性质：

　　　　1. 存在唯一性

　　　　　　意思就是说，对于每一个数而言，一定存在且只存在一个数，是他的逆元。

　　　　　　关于存在性：

　　　　　　　　由于 p 是质数，所以 a 和 p 一定是互质的，那么显然一定存在至少一个逆元。

　　　　　　那么我们来证明一下唯一性。

　　　　　　证明： 假设对于一个数a，有两个不同的逆元 a' 和 a^''

　　　　　　　　

　　　　　　　　不妨先设 a' < a'' 且 a'' - a' =k

　　　　　　　　由于 a ≠ 0 ，所以 k =0 (mod p).

　　　　　　　　所以 a’ 与 a''的值相等，即只有一个逆元

　　　　2.完全积性函数

　　　　　　意思是说，两个数的逆元的积等于这两个数积的逆元，即 inv[a]*inv[b]=inv[a*b] 。

　　　　　　证明：

　　　　　　　　

 

　　　　　　　　

　　　　　　　　

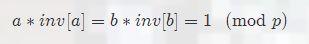
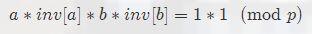
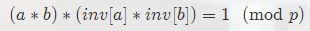
　　　　　　出现了，（a*b） 的逆元的定义。

　　　　3.a*inv[b]=a/b（mod p)

　　　　　　证明：

　　　　　　　　

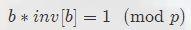
　　　　　　　　在两边都称上 a

　　　　　　　　

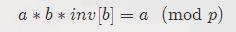
　　　　　　　　再把 b 除过去

　　　　　　　　

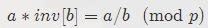
　　　　　　ok了。

　　　　　　这个性质非常重要：当需要算出 a/b mod p 的值时，使用朴素的方法，我们只能在 a 上不断加 p ，直到它能被 b 整除为止。

　　　　　　　　　　　　　　　但是当 a,b,p 都很大的时候，这种方法就GG了，但如果有了逆元，我们就可以 “ 非常方便，快捷 ” 地求解。

　　二.求法

　　　　说这么多我还没说怎么求。【等于没说

　　　　垃圾枚举几乎题题爆炸，这里就不说了。

　　　　1.费小

　　　　　　我们都知道费马小定理：：当 p 为素数时， a^{p-1}=1 (mod p) 。

　　　　　　那么 a*a^{p-2}=1 (mod p) 。

　　　　　　所以我们只需要快速幂求出 a^（p-2）就ok

 　　　　2.扩欧

　　　　　　仔细想想，发现其实我们寻找 a*x=1 （ mod p ）的解就相当于寻找方程 a*x+p*y=1 的解。

　　　　　　我们知道 扩展欧几里得 ax+by=c

　　　　　　好的，确定 a 和 p 互质，可以用了。

　　　　3.欧拉筛

　　　　　　我没用过，引用一段话：

　　如果我们要求出 1 ~ p-1 所有数的逆元呢？

　　还记得逆元是完全积性函数吗？所以对于每个合数 a ，我们把所有它的因子的逆元筛出来再相乘即可。

　　所以我们可以直接把所有素数筛出来，对它们求逆元（二或三），再把它的逆元乘给它的倍数就可以了。

　　　　4.线性递推

　　　　　　这个很常用的。【至少我常用

　　　　  　

　　　　　　因为很难写，我就直接放图片了。

---

后记

　　基本上全了，没有代码辅助，因为我也学的很浅显，并不是每一种都写过。

　　真的很遗憾，快NOIP了才意识到自己会的并不多，感觉要GG怎么办QAQ　　

　　希望能多补救一点吧。

　　祝大家RP+++++++++++++++++++++++++++。