【DP】那一天我们许下约定
题目描述
那一天我们在教室里许下约定。
我至今还记得我们许下约定时的欢声笑语。我记得她说过她喜欢吃饼干,很在意自己体重的同时又控制不住自己。她跟我做好了约定:我拿走她所有的饼干共N块,在从今天起不超过D天的时间里把所有的饼干分次给她,每天给她的饼干数要少于M以防止她吃太多。
当然,我们的约定并不是饼干的约定,而是一些不可言状之物。
现今回想这些,我突然想知道,有多少种方案来把饼干分给我的她。
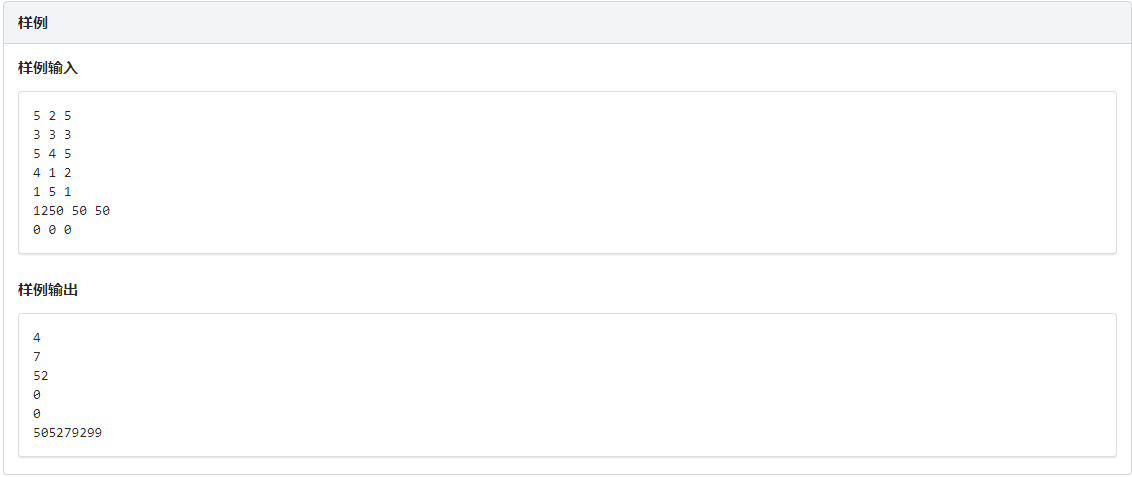
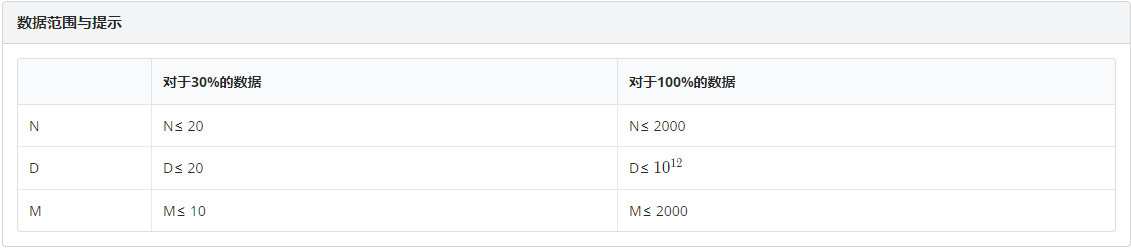
输入格式
每个测试点有多组测试数据。数据组数T≤10
对于每组数据,有一行共三个整数N,D,MN,D,MN,D,M含义如题。
输入结束标识为 “0 0 0” (不含引号)。
输出格式
对于每组数据,输出一行共一个整数,表示方案数对 998244353 取膜后的结果。
背景
关于这道题,是昨天的考试,至于考试为什么没有打,就应该是睡过头的锅了。
但是让我打我也不会啊 【滑稽
其实我一开始就打了一个n3的Floyed,发现20分,我也没管,觉得暴力20分挺正常。【这里有Floyed判最小环的题及讲解--->戳这里呢
但是优化以后就全wa了,检查之后发现反了一个很奇怪的错误。
思路分析
我们来观察一下题面,其中有一句话。
我拿走她所有的饼干共N块,在从今天起不超过D天的时间里把所有的饼干分次给她,每天给她的饼干数要少于M以防止她吃太多。
首先,我们会发现这种方案数之间,可能是有一些递推关系的。
所以采取DP的做法。
其次我们会发现一个性质:
这个人为了减肥,在少吃,最多能吃n天。
所以假设![]()
那么很显然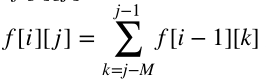 。
。
所以这是要打一个n3的暴力,然后像我一样的WAWAWAWA?
显然不是,2000的3次方是绝对会死的。
那么我们来考虑一下怎么优化。
究竟有什么地方是可以被省略的呢?
for (i)
for(j)
for(k) ???????????
感觉没毛病 啊,没什么多余的????????
开始陷入迷茫,算了算了,假算法,弃了弃了?
?????????????????????
怎么能这样?
不就是需要把中间的某一位省掉嘛?这还不简单?
第一维是天数,不能动。
第二维是饼干数,也不能动。
想也不用想,铁定省去第三维。
?仔细想想,对于 f [ i-1][...] 求和,你想到了什么?
前缀和啊,来了来了。
所以我们在循环中维护一个前缀和,就可以 O(1)的转移了。

这题的大思路就是这样。
细节坑点
其实上面的部分很多人都想到了【当然不包括我
但是却AC不能,这是为什么呢?
其实就一个,边界问题。
看到这里就先别往下翻,先对着自己的代码好好想想每一重循环的边界。
然后我们继续说。
首先是第一重:
循环边界 1~n ? 1~d ?
刚刚说过,最多只能是n天,但是实际上n与d的关系是不确定的。
所以此时边界应该是 1~min(n,d)
剩下的先别看。
然后是第二重:
循环边界 1~n ?
不是吗?开始疑神疑鬼? 莫非是 0~n? i~n?
交一交,发现都是对的。
???我来解释一下这是为什么。
原因就是组合数Cqi在q小于i的情况下,值为0
??????那 1~min(i*m-i,n) 行不行啊 ?
然后你就发现wa了。
???每天最多吃(m-1)个,吃 i 天没毛病啊?
我还没理解为什么如果可以解释请留言
对不起是由于sum转移的问题,是我傻了
然后是一个小小的优化:
if(!d||(n/d>=m)||(m==1)) { cout<<"0"<<endl; continue; }
刚刚还有一个人问我为什么前缀和要减到 sum[ i-1] [j-m] 而不是 sum[ i-1][ j-m+1]
我只想说看看题好嘛?每天吃少于m的,是吃不到m个的,所以你的 j-m+1实际上就是j-m
代码来了
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const long long mod=998244353;
long long d,jc[2010],ny[2010],fm[2010];
long long ans,n,m,sum[2010][2010];
long long f[2010][2010];
long long ks(long long x,long long k) {
long long num=1;
while(k){
if(k&1)num=num*x%mod;
x=x*x%mod;
k>>=1;
}
return num;
}
int main()
{
while(scanf("%lld%lld%lld",&n,&d,&m)&&n) {
memset(f,0,sizeof f);
ans=0;
memset(ny,0,sizeof ny);
memset(jc,0,sizeof jc);
memset(fm,0,sizeof fm);
fm[1]=d%mod;
for(int i=2;i<=n;i++)
fm[i]=(fm[i-1]*((d-i+1)%mod))%mod;
jc[1]=1;
for(int i=2;i<=n;i++)
jc[i]=(jc[i-1]*i)%mod;
ny[n]=ks(jc[n],mod-2);
for(int i=n-1;i>=1;i--)
ny[i]=(ny[i+1]*(i+1))%mod;
f[0][0]=1;
for(int i=0;i<=n;i++)
sum[0][i]=1;
for(int i=1;i<=min(n,d);i++) {
for(int j=1;j<=n;j++) {
if(j-m+1>0)
f[i][j]=((sum[i-1][j-1]-sum[i-1][j-m])%mod+mod)%mod;
else
f[i][j]=sum[i-1][j-1]%mod;
sum[i][j]=(sum[i][j-1]+f[i][j])%mod;
}
ans=(ans+((f[i][n]*ny[i]%mod)*fm[i]%mod)%mod)%mod;
}
printf("%lld\n",ans);
}
return 0;
}
