【Tarjan】通讯
题面
“这一切都是命运石之门的选择。”
试图研制时间机器的机关SERN截获了中二科学家伦太郎发往过去的一条短 信,并由此得知了伦太郎制作出了电话微波炉(仮)。
为了掌握时间机器的技术,SERN总部必须尽快将这个消息通过地下秘密通讯 网络,传达到所有分部。
SERN共有N个部门(总部编号为0),通讯网络有M条单向通讯线路,每条线 路有一个固定的通讯花费Ci。
为了保密,消息的传递只能按照固定的方式进行:从一个已知消息的部门向 另一个与它有线路的部门传递(可能存在多条通信线路)。我们定义总费用为所 有部门传递消息的费用和。
幸运的是,如果两个部门可以直接或间接地相互传递消息(即能按照上述方 法将信息由X传递到Y,同时能由Y传递到X),我们就可以忽略它们之间的花费。
由于资金问题(预算都花在粒子对撞机上了),SERN总部的工程师希望知道, 达到目标的最小花费是多少。
输入格式
多组数据,文件以2个0结尾。
每组数据第一行,一个整数N,表示有N个包括总部的部门(从0开始编号)。 然后是一个整数M,表示有M条单向通讯线路。
接下来M行,每行三个整数,Xi,Yi,Ci,表示第i条线路从Xi连向Yi,花费为 Ci。
输出格式
每组数据一行,一个整数表示达到目标的最小花费。

数据范围与提示
样例解释
第一组数据:总部把消息传给分部1,分部1再传给分部2.总费用:100+50=150.
第二组数据:总部把消息传给分部1,由于分部1和分部2可以互相传递消息,所以分部1可以无费用把消息传给2.总费用:100+0=100.
第三组数据:总部把消息传给分部1,最小费用为50.总费用:50.
数据范围
对于10%的数据,保证M=N-1
对于另30%的数据,N ≤ 20 ,M ≤ 20
对于100%的数据,N ≤ 50000 ,M ≤ 10^5 ,Ci ≤ 10^5 ,
数据组数 ≤ 5
数据保证一定可以将信息传递到所有部门。
背景
就在昨天,HZ的模拟赛将我惨惨的血虐,考完还特别认真的去打了tarjan的模拟赛。
今天就又被HZ教做人了。。。。
虽然没有爆零,但是这么简单的题面会爆零才怪了啊¿
所以我就来整理一下今天题目中最简单的一道吧。
其实这题要是想要找到正确的解法简直不要太简单。
但是写对就不容易了啊。
思路分析
首先,我们先观察题面。
然后我们就可以发现一个有趣的东西。
如果两个部门可以直接或间接地相互传递消息就可以忽略它们之间的花费。
纳尼???????
举个例子吧。
假如a->b, b->c, a->c,所以a,b,c之间的花费就没了?
那么这个时候如果有一个d->c,
引申一下,岂不是d->a 就相当于d->c?
好啊,抽象理解一下,a是不是就相当于c?
来了来了,思路来了。
当一张图上面出现有好几个点是等效的,并且这些点之间直接或间接联通(即DAG)。
??????这不是缩点嘛?
好的,那么我们假设思路的第一步就是缩点。【tarjan写错就死定了
接下来就出现了一个新的问题,既然缩点了,那么对于一个大点【我把一堆点缩点之后的点称为大点 来说,究竟把哪一条边作为边才是最优的?
??????想到 kruskal 求最小生成树的人快去好好看看图题面,这是一张有向图。
我们来看一张图理解一下。
构造是
6
1 2 1
3 1 5
2 3 4
4 2 6
5 1 3
3 6 9
画出图来应该是这样的 ↓
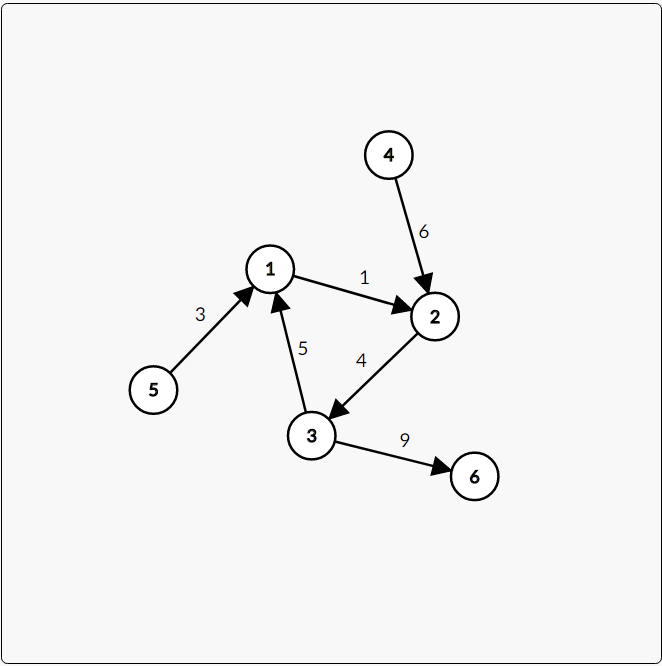
这张图 ↑ 缩点之后变成了这样 ↓
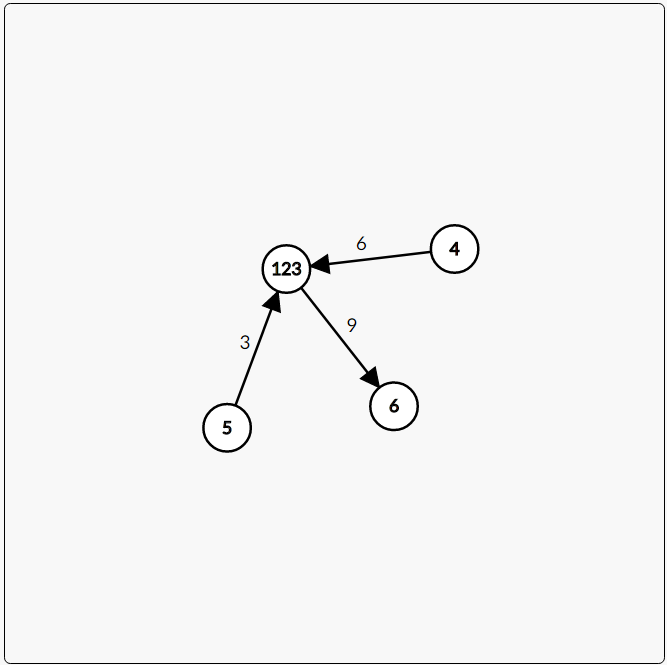
从上面这张图上我们可以发现,
其实,对于一个强连通分量来说,只要找到向他连的边中最小的就ok了。
最后是一点小小的忠告
在连边的时候,不如将所有点的编号都后移一位,使得控制中枢的编号成为1,方便时候的代码书写,还不容易错。
综上所述,本题思路就是在一张图中,联通染色,相同颜色取最小边。然后加起来就ok了。
代码实现
我知道你们只看这个。。。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define ll long long
using namespace std;
const int MA=1e5+10;//算上总部所以开大一点
int n,m;
int head[MA],ecnt;
struct ss{
int to,nxt,val;
}xl[MA*2];
void add(int a,int b,int c) {
xl[++ecnt].nxt=head[a];
xl[ecnt].to=b;
xl[ecnt].val=c;
head[a]=ecnt;
return;
}
int dfn[MA],low[MA],ti,p;
int sk[MA],col[MA],cnt;
bool vis[MA];
void Tar(int nw) {
dfn[nw]=low[nw]=++ti;
sk[++p]=nw;
vis[nw]=1;
for(int i=head[nw];i;i=xl[i].nxt) {
int nx=xl[i].to;
if(!dfn[nx]) {
Tar(nx);
low[nw]=min(low[nw],low[nx]);
}
else if(vis[nx])
low[nw]=min(low[nw],dfn[nx]);
}
if(dfn[nw]==low[nw]) {
++cnt;
int v;
do {
v=sk[p--];
vis[v]=0;
col[v]=cnt;
}while(nw!=v);
}
return;
}
int mindis[MA];//缩点之后相当于一个点,那么就取向外连接的点中权值最小的做边
void qmin() {
for(int i=1;i<=n;i++) {
for(int j=head[i];j;j=xl[j].nxt) {
int to=xl[j].to;
if(col[i]!=col[to])
mindis[col[to]]=min(mindis[col[to]],xl[j].val);
}
}
return;
}
void mem() {
memset(head,0,sizeof head);
memset(dfn,0,sizeof dfn);
memset(vis,false ,sizeof vis);
memset(low,0,sizeof low);
memset(sk,0,sizeof sk);
memset(col,0,sizeof col);
memset(mindis,0x7f,sizeof mindis);
cnt=0;
ti=0;
ecnt=0;
p=0;
return;
}
int main()
{
while(scanf("%d%d",&n,&m)!=EOF&&n&&m) {
mem();
for(int i=1;i<=m;i++) {
int x,y,c;
scanf("%d%d%d",&x,&y,&c);
add(x+1,y+1,c);//总部编号是0,不好处理
}
for(int i=1;i<=n;i++)
if(!dfn[i])//部门之间直接或者间接连接就像是一个环一样
Tar(i);//环内部门不花费,直接缩点染色
qmin();
int ans=0;
for(int i=1;i<=cnt;i++) {
if(mindis[i]==0x7f7f7f7f)
continue;
ans+=mindis[i];
}
cout<<ans<<endl;
}
return 0;
}
AC啦啦啦~

