【等比数列】序列


题目如上,样例极水。。。。。
背景
2019.7.14
sdfz某蒟蒻选手参加了hzoj上的NOIP模拟测试3.
然后, 爆零了。
真是个悲伤的故事。。。。。
本来我算下复杂度是差不多是对的,最次可能就是TLE了。
结果是全部WA了。
??????????????
??????????????
??????????????
发生了什么?
考场分析
1. 这是一条由等比数列的其中一部分数随机排列而成的数列。
2. 这条数列是没有重复的数字的。
3.公比可能为 1。
4.这段序列的公比的值非常小 q<=1000
联想一下数学的解题思路,就可以想到:
判断几个数是不是能够构成等比数列,就是一个反复取模的问题。
那么举个例子来证明一下:
假设这里有3个数 a=a1,b=a1*q,c=a1*q2*b
那么如果让a与b取模,就会发现,只要a,b呈现倍数关系就一定会得到0
所以我们这个时候可以取出b/a的值,记为x
x=b/a,这个时候的x就是这个等比数列的公比的某次方。
同样,我们对于b,c也重复这样的过程,得到y=c/b
接下来就是将a与c的关系建立起来了。
那么接下来是不是要取a和c的模呢?
答案当然是否定的,【不然如果数字的数量多了的话怎么办啊?
先感性猜测一下,如果是把x与y取模的话,会发生什么呢?
首先,a和c都是可以用b来表示出来的
那么x和y也是可以在同乘一个数之后得到b的,
那么x和y就相当于是a和c对于b的一个 映射?或者说叫代表?
所以自然结论就是采取x和y取模的方法。
还是刚刚那个例子,将x和y取模.
如果得到0,那么x与y呈现 xk=y 的结果,自然就是三个数呈现等比关系
如果不是那么肯定不是。
故而可以枚举第一个数的位置,将它作为a,对于之后的数进行枚举处理。
成熟思路
俗话说的好啊,有了小思路,就一定能向大方向扩展。 【雾
刚刚讲到要反复取模,这个时候就可以发现,其实是有冗余的部分的。
仔细想想会发现,假如一个数列特别长,然后这种数列还特别多
那么对于一个数来说有可能会反反复复计算好几回。
所以肯定不是正解。【NOIP模拟赛怎么可能是一道模拟题??
对于题面的分析的时候我们发现,公比可能是一个素数,也可能不是。
然后再次回到取模的问题上。
既然是NOIP模拟赛,怎么可能不考一种算法呢?【强词夺理
细细回顾之前的算法,有哪个是反复取模的过程?
emmmm......

bingo!gcd!
可是gcd和取公比又有什么关系呢?
????????????????????????
????????????????????????
????????????????????????
开始暴躁。。。。
这个时候我们不妨仔细回顾一下辗转相除法,
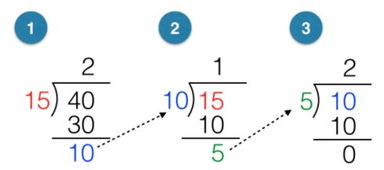
发现了嘛?
是不是和我们刚才取公比的过程惊人的相似?
那么结论就出现了,可以优化求公比的过程。
ll hgcd(ll a,ll b) {
ll r;
while(b>1) {
while(!(a%b)&&b!=1)
a/=b;
r=a;
if(r>b)
return -1;
a=b;
b=r;
}
return a;
}
那么既然找到公比,我们就可以直接向后判断了啊。
当然找到的公比很可能还能分解,但是这里就不需要了。
细节注意
1. 期间要多次注意公比为1的情况。
2. % 后面的数字不能比前面的大,不然就算是倍数也会得到值。
3. 素数筛一定要写对!!!!!!!!!!!!!!!!不然还不如copy一个素数表
4. 对于怎么应用上面的部分,直接双指针枚举 l,粘出来一段进行上面的操作就ok了。
代码实现
我知道你们只看这个。。。。。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define ll long long
using namespace std;
int n,ans=0;
int tot;
ll a[100010],b[70],x[70],d[60000];
int prime[1001]={2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,
107,109,113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199,211,223,
227,229,233,239,241,251,257,263,269,271,277,281,283,293,307,311,313,317,331,337,347,
349,353,359,367,373,379,383,389,397,401,409,419,421,431,433,439,443,449,457,461,463,
467,479,487,491,499,503,509,521,523,541,547,557,563,569,571,577,587,593,599,601,607,
613,617,619,631,641,643,647,653,659,661,673,677,683,691,701,709,719,727,733,739,743,
751,757,761,769,773,787,797,809,811,821,823,827,829,839,853,857,859,863,877,881,883,
887,907,911,919,929,937,941,947,953,967,971,977,983,991,997,-1};
ll hgcd(ll a,ll b) {
ll r;
while(b>1) {//%后的数必须小
while(!(a%b)&&b!=1)
a/=b;
r=a;
if(r>b)
return -1;
a=b;
b=r;
}
return a;
}
bool pd(int l,int r) {
if(l==r)
return 1;
bool flag=0;
for(int i=l;i<=r;i++) {
b[i-l]=a[i];
if(i!=l&&a[i]!=a[i-1])
flag=1;
}
if(!flag)
return 1;//如果公比为1
int len=r-l+1;
sort(b,b+len);//注意复制的时候没有改变位置
for(int i=1;i<len;i++) {
if(b[i]%b[i-1]!=0)
return 0;
x[i-1]=b[i]/b[i-1];//x是公比数组
if(x[i-1]==1)
return 0;//如果x==1,说明公比为1
}
ll Gcd=x[0];
for(int i=1;i<len-1;i++) {
Gcd=hgcd(Gcd,x[i]);
if(Gcd==-1)
return 0;
}
for(int i=0;prime[i]!=-1;i++)
if(!(Gcd%prime[i])) //筛
return 1;
return 0;
}
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++)
scanf("%lld",&a[i]);//从头存方便筛/复制
int l=0,r=0;
while(l<(n<<1)) {
if(pd(l,r)) {
ans=max(ans,r-l+1);
++r;
if(r==n) {
--r;
++l;
}
}
else
++l;
}
cout<<ans<<endl;
return 0;
}
完了完了,皆大欢喜!!!

