关于分块的个人理解(二)

时隔多日，终于又想起来要写题解了啊 ！！！

分块的基本知识和概念都在(一)中讲过了，那么我们今天就来看一些稍微有点难度的题目吧。

如果有什么要补充的我就穿插在题目里面讲了。

重要的分块特有的题型

　　基本上，大多数的分块的题目使用树状数组或者线段树都是可以做的，甚至更快更优秀

　　但是实际上分块存在的意义并不是为了服务于我们的懒惰，他是有一定的特殊意义的。

　　那么我们来思考一个问题：

　　　　　　现在有一个序列，给出几个询问，求问某段区间内的最大值。

　　对于这个问题，线段树可以做吗？当然可以，但是超级麻烦。

　　这个时候就是我们分块作用体现最大的时候了。

　　分块成为最优解-->不满足区间可加性的序列询问问题

---

例题

　　虽然比这道 [Violet]蒲公英 要简单的题还是有的，但是这道毕竟比较典型嘛。

题目背景

亲爱的哥哥：

你在那个城市里面过得好吗？

我在家里面最近很开心呢。昨天晚上奶奶给我讲了那个叫「绝望」的大坏蛋的故事的说！它把人们的房子和田地搞坏，还有好多小朋友也被它杀掉了。我觉得把那么可怕的怪物召唤出来的那个坏蛋也很坏呢。不过奶奶说他是很难受的时候才做出这样的事的……

最近村子里长出了一大片一大片的蒲公英。一刮风，这些蒲公英就能飘到好远的地方了呢。我觉得要是它们能飘到那个城市里面，让哥哥看看就好了呢！

哥哥你要快点回来哦！

爱你的妹妹 Violet

Azure 读完这封信之后微笑了一下。

“蒲公英吗……”

题目描述

在乡下的小路旁种着许多蒲公英，而我们的问题正是与这些蒲公英有关。

为了简化起见，我们把所有的蒲公英看成一个长度为n的序列 (a_1,a_2..a_n)(a1​,a2​..an​)，其中 a_iai​ 为一个正整数，表示第i棵蒲公英的种类编号。

而每次询问一个区间 [l,r]，你需要回答区间里出现次数最多的是哪种蒲公英，如果有若干种蒲公英出现次数相同，则输出种类编号最小的那个。

注意，你的算法必须是在线的

输入输出格式

输入格式：

第一行两个整数 n,m ，表示有n株蒲公英，m 次询问。

接下来一行n个空格分隔的整数 a_iai​ ，表示蒲公英的种类

再接下来m 行每行两个整数 l_0,r_0l0​,r0​，我们令上次询问的结果为 x（如果这是第一次询问， 则 x=0）。

令 l=(l_0+x-1)\bmod n + 1,r=(r_0+x-1) \bmod n + 1l=(l0​+x−1)modn+1,r=(r0​+x−1)modn+1，如果 l>r，则交换 l,r 。

最终的询问区间为[l,r]。

 

输出格式：

输出m 行。每行一个整数，表示每次询问的结果。

输入输出样例

输入样例#1：

6 3 
1 2 3 2 1 2 
1 5 
3 6 
1 5

输出样例#1：

1
2
1

解法：

　　强制在线啊，区间最大值啊。

　　是很完美的卡掉莫队和线段树的题面啊。

　　那么我们选择采用分块做法。

　　首先将区间L~R分成三段，分开处理。

　　　　1.整块 l ~ r 。

　　　　2.前端不满。

　　　　3.后端不满。

那么，很显然 -->  maxn = max { cnt[ 2. /3. ] , maxn[ l ~ r ] };

 　　现在我们需要考虑的就是如何暴力处理以最小代价了。

解法一：

　　

 　　

解法二：

　　

---

之前一直都没介绍怎么计算块的大小，那就这道题补上吧。

块的大小计算

　　计算块的大小主要就是根据时间复杂度，防止一不小心就 T 了之类的。

　　那么就用事实说明吧（感觉更有说服力一点）

　　　　　　如果有错误一定要告诉我~

---

 

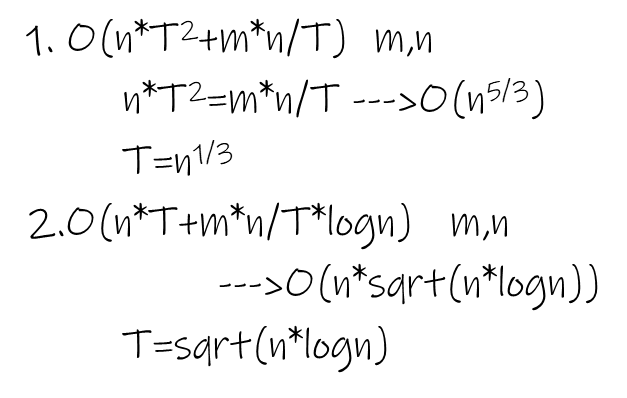
 另外这题还能水过！！！luogu AC大法

　　　　离散化+暴力处理区间众数 + luogu氧气优化！！

O₂真好~~~我爱！！

---

 

奉上代码

　　因为我比较菜所以解法二的代码不是我的~~我也不知道是谁的 /无奈

　解法一

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;

const int MA=40001;
const int u=41;
int c[u][u][MA],f[u][u],d[u][u];
int a[MA],b[MA],fa[MA],fb[MA];
int st[u],ed[u];
int n,m,t,l,tot;
int x,y,ans,L,R,cnt,num;

void pw() {
    t=(int)pow(n*1.0,1.0/3);
    if(t) 
        l=n/t;
    for(int i=1;i<=t;i++) {
        st[i]=(i-1)*l+1;
        ed[i]=i*l;
    }
    if(ed[t]<n) {
        st[t+1]=ed[t]+1;
        ed[++t]=n;
    }
    memcpy(fa,a,sizeof(a));
    sort(fa+1,fa+n+1);
    for(int i=1;i<=n;i++)
        if(i==1||fa[i]!=fa[i-1]) 
            fb[++tot]=fa[i];
    for(int i=1;i<=n;i++) 
        b[i]=lower_bound(fb+1,fb+tot+1,a[i])-fb;
    for(int i=1;i<=t;i++)
        for(int j=i;j<=t;j++) {
            for(int k=st[i];k<=ed[j];k++) 
                c[i][j][b[k]]++;
            for(int k=1;k<=tot;k++)
                if(c[i][j][k]>f[i][j]||c[i][j][k]==f[i][j]&&k<d[i][j]) {
                    f[i][j]=c[i][j][k];
                    d[i][j]=k;
                }
        }
    return;
}

inline void upd(int i) {
    c[L][R][b[i]]++;
    if(c[L][R][b[i]]>cnt||c[L][R][b[i]]==cnt&&b[i]<num) {
        cnt=c[L][R][b[i]];
        num=b[i];
    }
}

int solve(int x,int y) {
    int r;
    if(x>y) swap(x,y);
    for(int i=1;i<=t;i++) 
        if(x<=ed[i]) {
            l=i; 
            break;
        }
    for(int i=t;i;i--) 
        if(y>=st[i]) {
            r=i; 
            break;
        }
    if(l+1<=r-1) {
        L=l+1;
        R=r-1;
    } 
    else L=R=0;
    cnt=f[L][R];
    num=d[L][R];
    if(l==r) {
        for(int i=x;i<=y;i++) 
            upd(i);
        for(int i=x;i<=y;i++) 
            c[L][R][b[i]]--;
    }
    else {
        for(int i=x;i<=ed[l];i++) 
            upd(i);
        for(int i=st[r];i<=y;i++) 
            upd(i);
        for(int i=x;i<=ed[l];i++) 
            c[L][R][b[i]]--;
        for(int i=st[r];i<=y;i++) 
            c[L][R][b[i]]--;
    }
    return fb[num];
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) 
        scanf("%d",&a[i]);
    pw();
    for(int i=1;i<=m;i++) {
        scanf("%d%d",&x,&y);
        ans=solve((x+ans-1)%n+1,(y+ans-1)%n+1);
        printf("%d\n",ans);
    }
    return 0;
}

解法二：

#define FILEIO

#define INPUT "dandelion.in"
#define OUTPUT "dandelion.out"

#include <set>
#include <map>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cctype>
#include <vector>
#include <cassert>
#include <cmath>

#define mp make_pair
#define pb push_back
#define foreach(i,T) for(__typeof(T.begin()) i = T.begin(); i != T.end(); ++i)

using namespace std;

namespace Solve {
	const int MAXN = 40013;
	const int MAXM = 36;

	inline int ScanInt(void) {
		int r = 0, c, d;
		while (!isdigit(c = getchar()) && c != '-');
		if (c != '-') r = c - '0'; d = c;
		while ( isdigit(c = getchar())) r = r * 10 + c - '0';
		return d=='-'?-r:r;
	}

	int n, m, a[MAXN], cnt = 0, p, belong[MAXN], t, fim[MAXN];
	set<int> S; map<int, int> M;

	inline void Input(void) {
		n = ScanInt(), m = ScanInt(), p = pow(n, 0.666666666666), t = n / p; if (n % p != 0) t++;
		for (int i = 1; i <= n; i++) S.insert(a[i] = ScanInt());
		foreach(it, S) M[*it] = ++cnt;
		for (int i = 1; i <= n; i++) fim[M[a[i]]] = a[i], a[i] = M[a[i]];
	}

	inline void Update(int t, int v, int &Max, int &pos) {
		if (v == Max && t < pos) pos = t;
		if (v > Max) pos = t, Max = v;
	}

	struct Node {
		int c[MAXN], pos, Max;
		inline void operator +=(const int t) {
			c[t]++;
			Update(t, c[t], Max, pos);
		}
		inline void operator -=(const int t) {
			c[t]--;
		}
	}f[MAXM][MAXM];

	int C[MAXM][MAXN];

	inline void Init(void) {
		for (int i = 1; i <= n; i++) {
			if ((i - 1) % p == 0) belong[i] = belong[i - 1] + 1; else belong[i] = belong[i - 1];
			C[belong[i]][a[i]]++;
		}
		for (int i = 1; i <= t; i++) {
			for (int j = i; j <= t; j++) {
				for (int k = 1; k <= cnt; k++) 
					f[i][j].c[k] = f[i][j - 1].c[k] + C[j][k];
				for (int k = 1; k <= cnt; k++) 
					Update(k, f[i][j].c[k], f[i][j].Max, f[i][j].pos);
			}
		}
	}

	int hash[MAXN];

	inline int Cal(int l, int r) {
		int L = belong[l], R = belong[r];
		if (L == R) {
			int Max = 0, pos = 0;
			for (int i = l; i <= r; i++) {
				hash[a[i]]++;
				Update(a[i], hash[a[i]], Max, pos);
			}
			for (int i = l; i <= r; i++) hash[a[i]]--;
			return fim[pos];
		}
		if (belong[l] == belong[l - 1]) L++;
		if (belong[r] == belong[r + 1]) R--;
		int b = f[L][R].pos, u = f[L][R].Max;
		for (int i = l; belong[i] == belong[i - 1]; i++) f[L][R] += a[i];
		for (int i = r; belong[i] == belong[i + 1]; i--) f[L][R] += a[i];
		int ret = fim[f[L][R].pos];
		for (int i = l; belong[i] == belong[i - 1]; i++) f[L][R] -= a[i];
		for (int i = r; belong[i] == belong[i + 1]; i--) f[L][R] -= a[i];
		f[L][R].pos = b, f[L][R].Max = u;
		return ret;
	}

	inline void solve(void) {
		Input();
		Init();
		int x = 0;
		for (int i = 1; i <= m; i++) {
			int l = ScanInt(), r = ScanInt();
			l = (l + x - 1) % n + 1, r = (r + x - 1) % n + 1;
			if (l > r) swap(l, r);
//			fprintf(stderr, "%d %d\n", l, r);
			printf("%d\n", x = Cal(l, r));
		}
	}
}

int main(void) {
	#ifdef FILEIO
		freopen(INPUT, "r", stdin);
		freopen(OUTPUT, "w", stdout);
	#endif
	Solve::solve();
	return 0;
}

解法三：

// luogu-judger-enable-o2
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<vector>
#include<map>
#define itn int
#define pos(x) (x+ans-1)%n+1
using namespace std;

const int MA=50001;
itn n,m,ans;
int l,r;
int a[MA],b[MA],ts[MA];

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) {
        scanf("%d",&a[i]);
        b[i]=a[i];
    }
    sort(b+1,b+n+1);
    int sum=unique(b+1,b+n+1)-b-1;
    for(int i=1;i<=n;i++) 
        a[i]=lower_bound(b+1,b+sum+1,a[i])-b;
    while(m--) {
        scanf("%d%d",&l,&r);
        l=pos(l);
        r=pos(r);
        if(l>r)
            swap(l,r);
        for(itn i=l;i<=r;i++) 
            ts[a[i]]++;
        int maxn=0,p=0;
        for(itn i=1;i<=sum;i++) {
            if(maxn<ts[i]){
                maxn=ts[i];
                p=i;
            }
        }
        cout<<b[p]<<endl;
        ans=b[p];
        memset(ts,0,sizeof ts);
    }
    return 0;
}

　　虽然抄了会AC，但是还是不要了啊！！

　　　　　　　　　　　　万一我一不小心就写挂了呢？

---

 

最后是相似题目的推荐！！题目均来源于luogu