CTSC2014 && 洛谷P4503 企鹅QQ

很好，我又来写题解了。

这次介绍的是一道叫做企鹅QQ的题目（洛谷给的标签是省选/NOI^-）其实我觉得没那么夸张啦（然而wa了3次 逃】）。

先放题面。

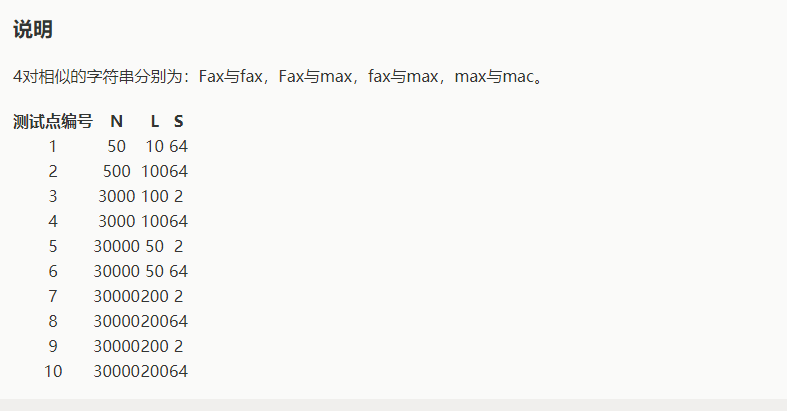
然后是数据，洛谷惯例？样例极水！

Input

 

4 3 64
Fax
fax
max
mac

 

Output

4

 

---

　　那么切入正题。

　　这题乍一看似乎很简单的样子，感觉思路很简单，暴力枚举每一位是不是一样就行。但是，这样的话肯定复杂度就上了O（n²），光速TLE；

　　那么我就要考虑一下更优的算法了-->将前缀和的思想加入到hash中。

　　然后分别按照从前往后的顺序和从后往前的顺序生成两个hash数组。这样用O(n)的时间就可以完成预处理。

 

　　然后我们考虑枚举哪一位是不相同的，比较将这一位删去后的串的hash值是否相等，那么这个hash值我们可以借助两个hash数组在O(1)的时间内算出来；

　　设这一位是j，那么我们只需要将hash1[j-1]和hash[j+1]的值加起来就可以得到删除掉一维之后的hashh值。

　　当然这两个hash数组都必须是二维的，上面的hash表示其中第二维，第一维的意义是字符串的编号。

 

　　然而，这就结束了吗？那可是 省选 谢谢。

　　如果在比较的时候，你写的很暴力的话，还是会TLE（亲身实践请勿模仿QAQ），所以我们使用sort将其排序，比较相邻的hash值，这样可以节省时间。

　　算法的总时间复杂度就是O(nl\log n)，差不多显然能过。

 

---

放上代码

#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<set>
using namespace std;
typedef unsigned long long ll;
int n,l,s,ans;
ll hh[30001],hsh[30001][201],hsh2[30001][201];
char a[30001][201];
void rd(int i) {
    for(int j=1;j<=l;j++) hsh[i][j]=hsh[i][j-1]*131+a[i][j];
    for(int j=l;j>=1;j--) hsh2[i][j]=hsh2[i][j+1]*137+a[i][j];
    return;
}
int main()
{
    scanf("%d%d%d",&n,&l,&s);
    for(int i=1;i<=n;i++) {
        scanf("%s",a[i]+1);
        rd(i);
    }
    for(int i=1;i<=l;i++) {
        for(int j=1;j<=n;j++) hh[j]=hsh[j][i-1]*233+hsh2[j][i+1]*211;
        sort(hh+1,hh+n+1);
        int sun=1;
        for(int j=1;j<n;j++) {
            if(hh[j]==hh[j+1]) {
                ans+=sun;
                sun++;
            }
            else sun=1;
        }
    }
    printf("%lld\n",ans);
    return 0;
}

虽然，我的这份代码在没有优化的情况下不是最优的（但是你会更优的又怎么会看题解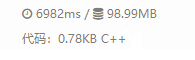？？）但是绝对AC没问题的。

并且，它在开启氧气（O₂）的情况下-->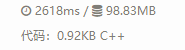

偷偷告诉你们，其实最优解第一个-->（感觉也没有快多少 ~？无耻.jpg）

所以加油啦！！