casper correct by construction 共识（一）

本文属作者原创，转载请注明出处：

http://www.cnblogs.com/qxred/p/casper.html

0. 参考资料

Casper Proof-of-Stake on RChain | RChain Developer Retreat Day 2 Casper Proof-of-Stake on RChain Part 2 | RChain Developer Retreat Day 2

本文是对rchain中capser共识算法casper correct by construction (casper CBC)的解释，原文来自
https://rchain.atlassian.net/wiki/spaces/CORE/pages/92536846/Casper+for+RChain

1. 一般性的Casper共识

首先我们来看比较难懂的开头这一段：

An "estimate safety consensus protocol" (the terminology will be made clear shortly) requires the following things:

1. a set of possible consensus values \(\mathbf{C}\), (i.e. we need to know what we're deciding on);
2. a logic, \(\mathcal{L}_{\mathbf{C}}\) , in which the propositions are true or false statements about elements of \(\mathbf{C}\);
3. a category, \(\Sigma\) , (in the mathematical sense, see Wikipedia for an overview) representing the protocol, where the objects in \(\Sigma\) are the protocol states and the morphisms are the protocol executions;
4. a function called the estimator which maps protocol states to propositions in the logic, \(\mathcal{E} : ob(\mathbf{\Sigma}) \rightarrow prop(\mathcal{L}_{\mathbf{C}})\)

We say that a proposition, \(p\), has estimate safety on a protocol state, \(\sigma\), if for all possible future states of \(\sigma\) the estimator implies \(p\). Given a few reasonable constraints on the logic and estimator (see original paper for details), we obtain the following consensus safety result: if \(\sigma_1\) and \(\sigma_2\) have a common future state then their safe estimates cannot be contradictory (i.e. if \(p\) has estimate safety on \(\sigma_1\) then \(\neg p\) cannot have estimate safety on \(\sigma_2\)). Therefore, if nodes act according to the estimator, they cannot reach states with views that are irreconcilable and hence consensus is always possible. Moreover, once a node sees that a proposition is safe, it knows that proposition will remain true for the final consensus as well.

这段话什么意思呢？举个例子，美国大选，选民投票决定特朗普是否连任。

这里，\(\mathbf{C}\)是一个元素的集合：\(\mathbf{C}=\) {特朗普连任}

选民可以投赞成或者反对，用文中的符号表示即：逻辑 \(\mathcal{L}_{\mathbf{C}}\)含有两个命题(proposition)：特朗普连任is true， 特朗普连任is false。

假如有5个选民，则每个选民的投票状态有3种：赞成，反对，未投票。所以这5个选民所有可能的投票状态有\(3^5\)种。假如当前的有2人投了反对票，则在第三个人投赞成票之后，状态发生了转移：{反对，反对，未投票，未投票，未投票} \(\rightarrow\) {反对，反对，赞成，未投票，未投票}。 这种状态转移可以看作一个函数 \(F_{赞成}\)，其输入是一个状态，输出也是一个状态。同样可以有函数 \(F_{反对}\)。所有投票状态的集合(含有\(3^5\)个状态)，以及状态转移函数集合{\(F_{赞成}\),\(F_{反对}\)}构成了一个范畴(Category)。Category(范畴) 简单来说就是一个集合加上这个集合上的操作。比如集合是整数，而操作是加、减、乘。注意除法不是，因为两个整数的除法可能不是整数。用文中的符号表示就是 objects in \(\Sigma\) = 所有整数，morphisms = 加法、减法、乘法。

我们根据当前的投票状态预测最终的投票结果叫做estimate，比如当前的投票状态为 {反对，反对，赞成，未投票，未投票} ，则我们会觉得最后特朗普最终连任失败的概率比较大。但不排除成功的可能。但是如果第4个选民投了反对票，则特朗普连任一定失败，因为无论第5个选民投什么，反对票已经占了多数。我们用estimator函数\(\mathcal{E}\)来表示这种估计，其输入是当前投票状态，而输出则是多数选民投票的结果。在第4个人投了反对票之后，特朗普一定连任失败，我们称命题“特朗普连任is false” 在状态 {反对，反对，赞成，反对，未投票}下是estimate safe的。

我们可以得到这样一个结论：状态\(\sigma_1\)={反对，反对，反对，未投票，未投票}由于是estimate safe，则其后续的任何状态\(\sigma_2\)={反对，反对，反对，反对，未投票}，或者\(\sigma_3\)={反对，反对，反对，赞成，未投票}，或者\(\sigma_4\)={反对，反对，反对，赞成，赞成}有相同的预测结果，而且命题“特朗普连任失败”都是estimate safe的。相应的，命题“特朗普连任成功”是不可能safe的。

根据这个结论，如果一个命题已经是estimate safe，则可以作出决定，提前结束选举。对应到block chain中，则是交易得到确认(finalize)，即保证以后不会撤销。

2. RChain中的Casper共识

BlockChain中，共识问题需要解决的问题是选取哪个块加入到链上。在bitcoin的Proof of Work (POW)共识中，所有矿工都以消耗的电力作为成本产生区块，而唯有首先解答出计算题的块被选入。所以我们可以理解为投入电力越多的矿工，其产生的块才越有可能被选中。在Casper中，则用抵押的币代替电力，一个验证者(Validator，相当于矿工)抵押越多的币，其产生的区块才越有可能被选中。

先考虑一个最简单的共识算法：验证者所有新产生的区块必须加到抵押总和最多的链上，如果一个链被所有验证者都在其后加载了块，则该链上所有的交易将永远不会被修改。

如图所示，假设有三个验证者: A,B,C，其中A上方的方块中的数字200表示目前以A产生的块结尾的那条链的押金总和，同理B,C。比如，创世块拥有100押金，而A,B,C各自产生了押金100,0,50的块，并分别加在创世块之后形成了3条链：

接着，A产生了新的块，押金为10。根据规则必须要加到押金总和最大的链上，这里有个问题，由于延时，A可能不知道验证者B，而只收到C的消息，在图中用虚线表示。当然A一定知道自己的链的押金情况。由于A押金200>C押金150，因此A的块加载到A链上，图中用实线表示：

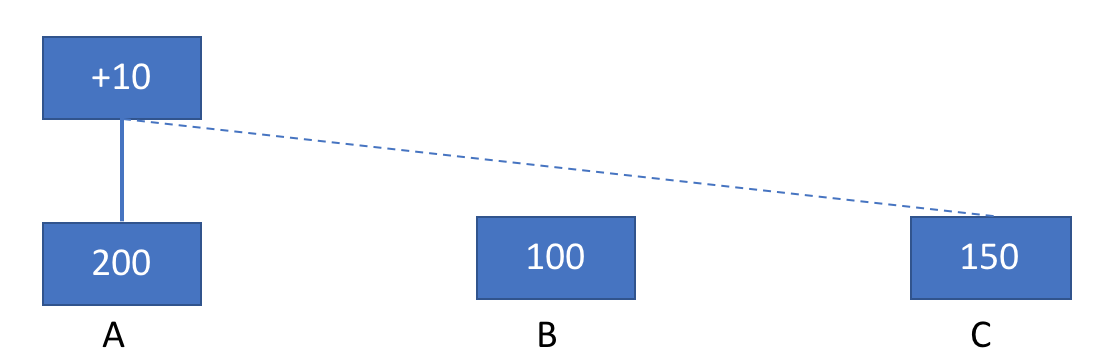
然后B产生一个块，押金为5，由于延时，B不知道A，只知道C，由于B链押金100小于C链押金150，因此块加入C链：

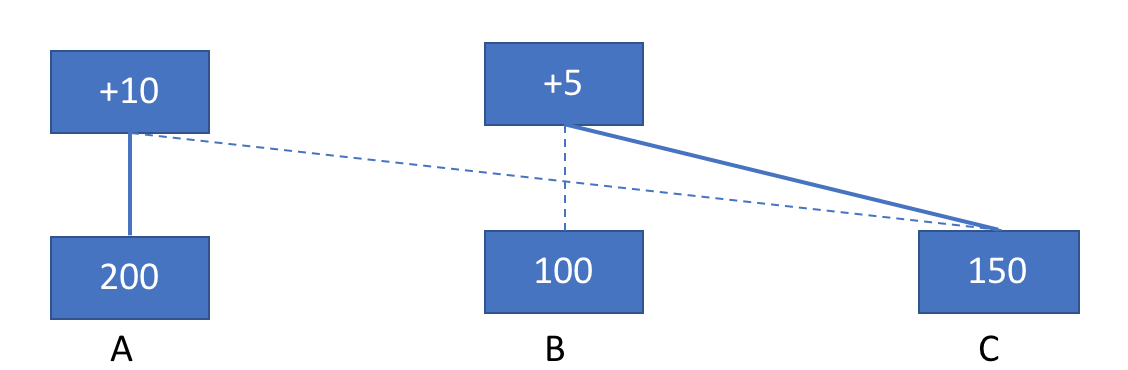
接下来B又产生一个块，押金为20，这时B收到了A的消息，比较之后A链胜出，因此加入A链

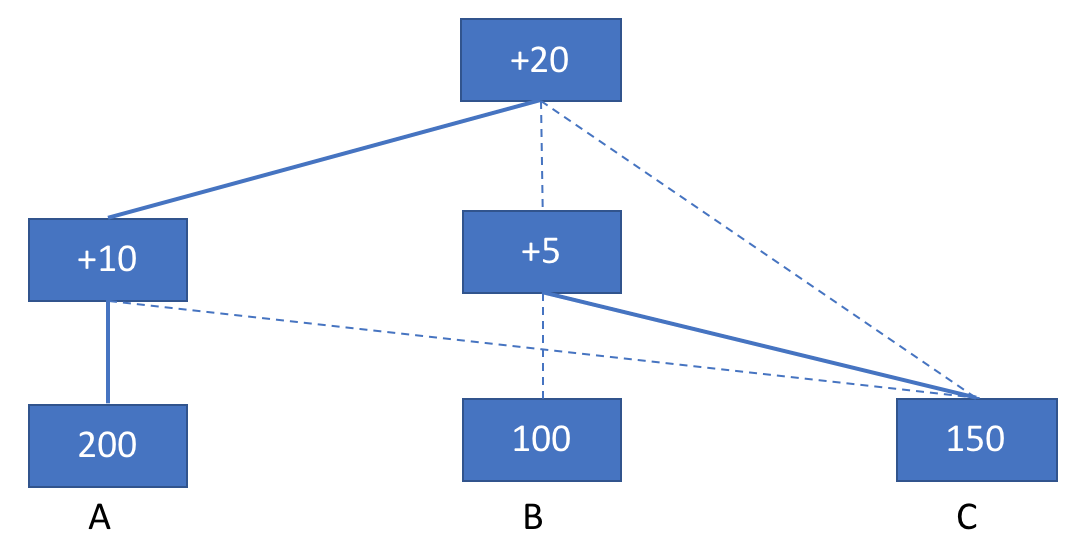
然后A产生一个押金为5的块，加入A链

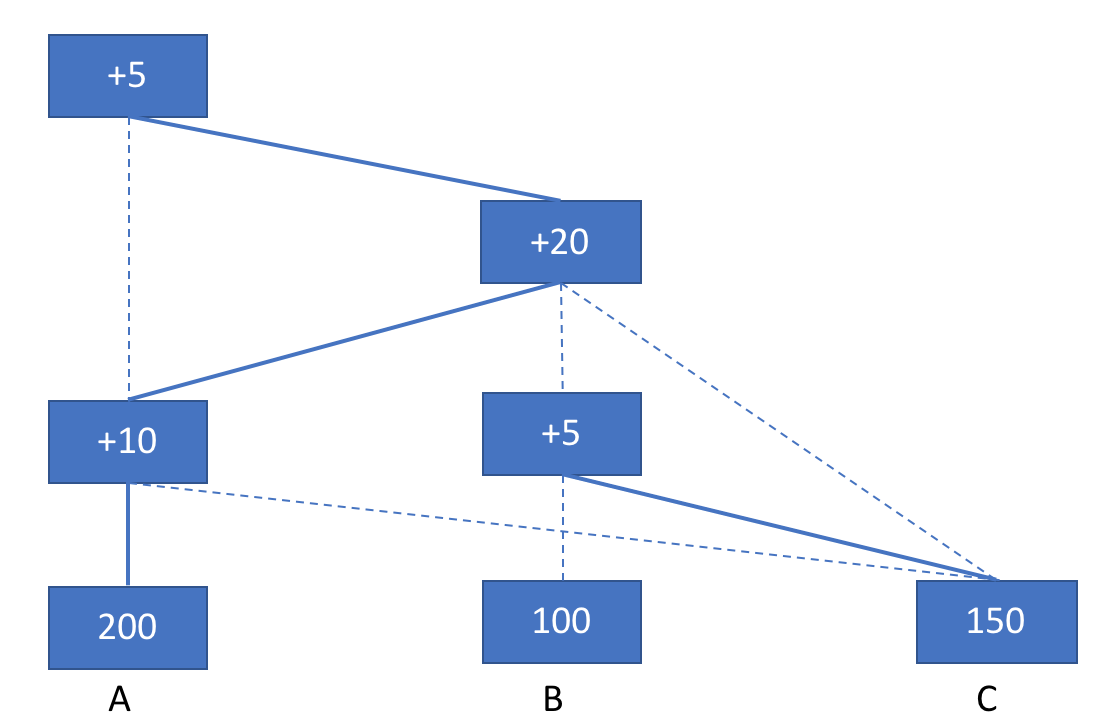
之后C产生一个押金为5的块，此时由于延时，C没有收到A的消息，C只知道B，比较之后加入B链。

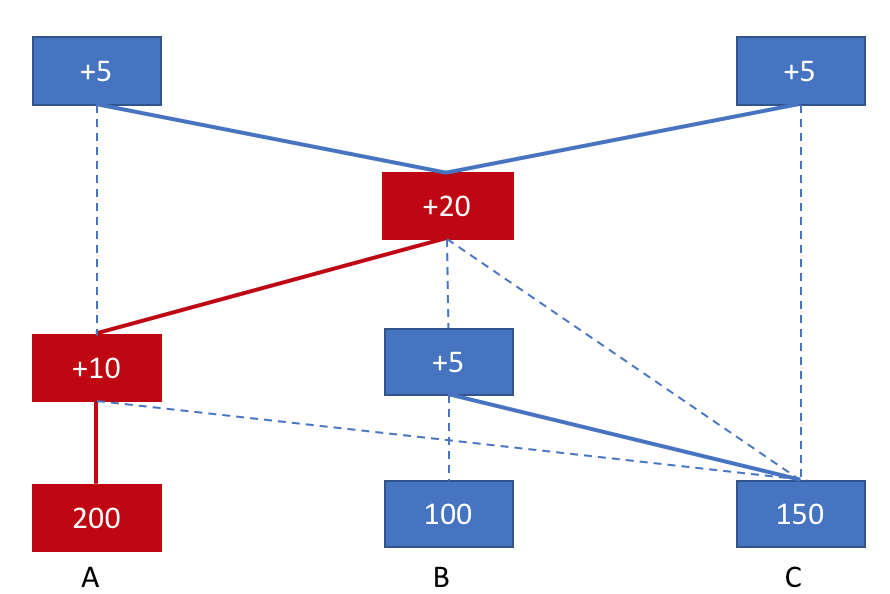
注意此时红色部分，接下来无论是A还是B还是C产生的新块，所追加的链都含有红色部分，因为红色部分是A链，B链，C链公共部分。因此可以安全地确认其中所含有的交易，不用担心今后会被撤销。

回到Estimate safety的定义：在当前的链状态下，命题“红色部分在将来不会被撤销is true”是estimate safe的。

需要指出的是，Casper共识产生的不是一个链，而是一个有向无环图(DAG)。

现在我们可以定义之前的符号了：

\(\mathbf{C}\)=所有DAG的集合，\(\mathcal{L}_{\mathbf{C}}\)=DAG中子图在将来是否会被撤销，Category(范畴)中元素集合\(ob(\Sigma)\) = DAG的状态，比如累计押金。操作morphisms：追加某个块从而形成新的DAG状态。而estimate safety在前面已经有所叙述。