casper correct by construction 共识(二)
本文属作者原创,转载请注明出处:
http://www.cnblogs.com/qxred/p/casper-2.html
1. Capser correct by construction (Casper CBC) 共识
本文是对rchain中capser共识的解释,原文来自 https://rchain.atlassian.net/wiki/spaces/CORE/pages/92536846/Casper+for+RChain上篇中那个最简单的共识模型存在以下问题:
- 如何设置奖励以鼓励更多用户参与。
- 如何控制奖励数量,以防止货币超发。
- 如何防止黑客。
本文将对原有的最原始模型进行改进。
首先,块的产生分为两步:
1 提议 (Propose):从验证者账号中扣除押金,并将押金放入块中。同时准备好块中的数据,数据包括:
- parent block pointer(s): 前驱块的Hash
- attached "political capital" (we'll get to where this comes from and what it is for shortly): 根据Greg在youtube视频里的解释,political capital (PC)是押金的函数。具体什么后面会解释,这里只需要明白一点,块的押金越多,PC越大,从而越有可能达成共识,获得奖励。
- data 有很多种,比如参与共识的验证者名单。
- justification (pointers to other blocks the validator had seen when this block was created) 简单说,就是在创建该块时,验证者所能看到的用于挑选押金最大的链的所有其他块。当然验证者为了加长自己链,可以假装看不见其他链。下面我们会看到这么做会减小他的PC,从而不容易被其他验证者确认。
2 确认 (Acknowledge): 验证区块,将块接入DAG中。具体来说,当前验证者只能从所有验证者的最新接入的块中挑一个或者多个作为新块的前驱,并且挑出的前驱块相互之间不能成为前驱。如下图所示,B新加了一个块(最上方的+5块),试图接入DAG。第二种接法是错的,因为B链的最后一块是C链的最后一块的前驱,第三种方法也是错的,因为接入的不是C的最后一块。
方法一:
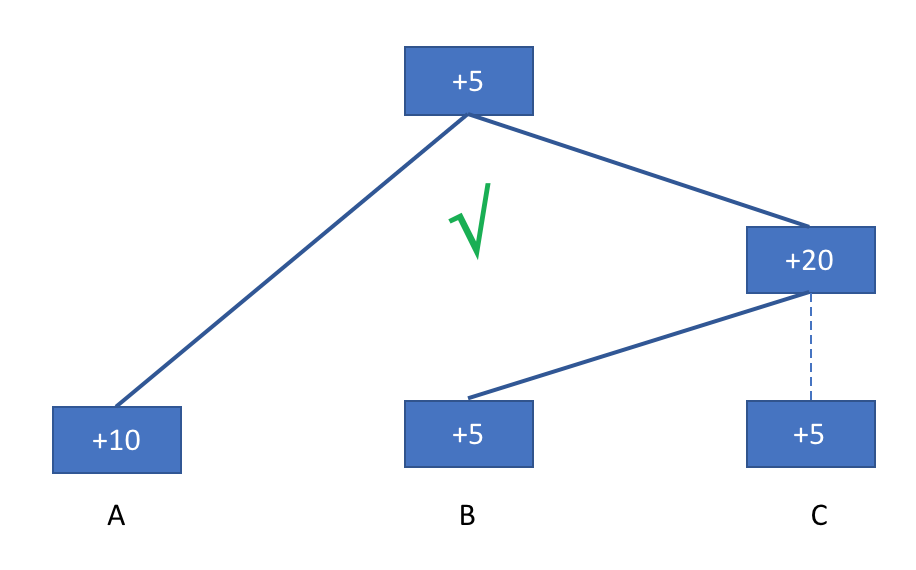
方法二:
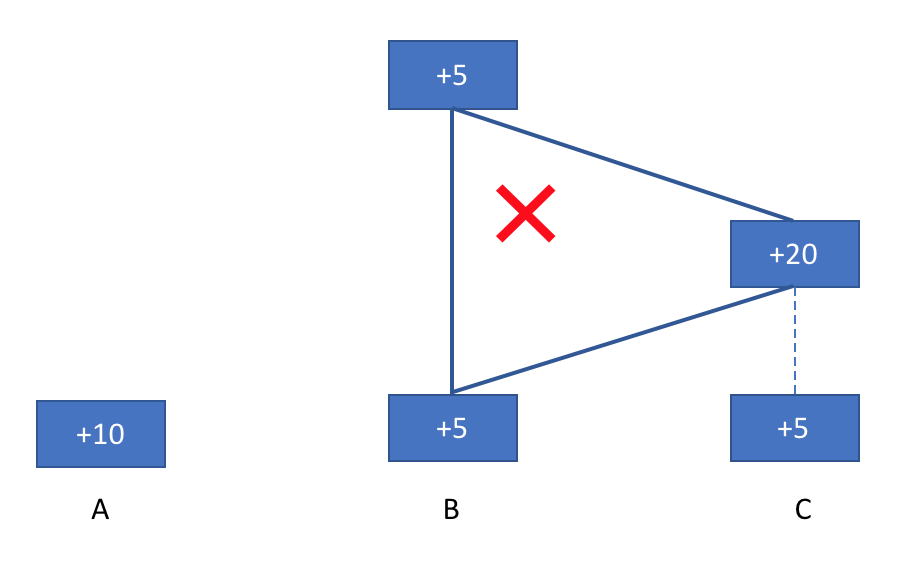
方法三:
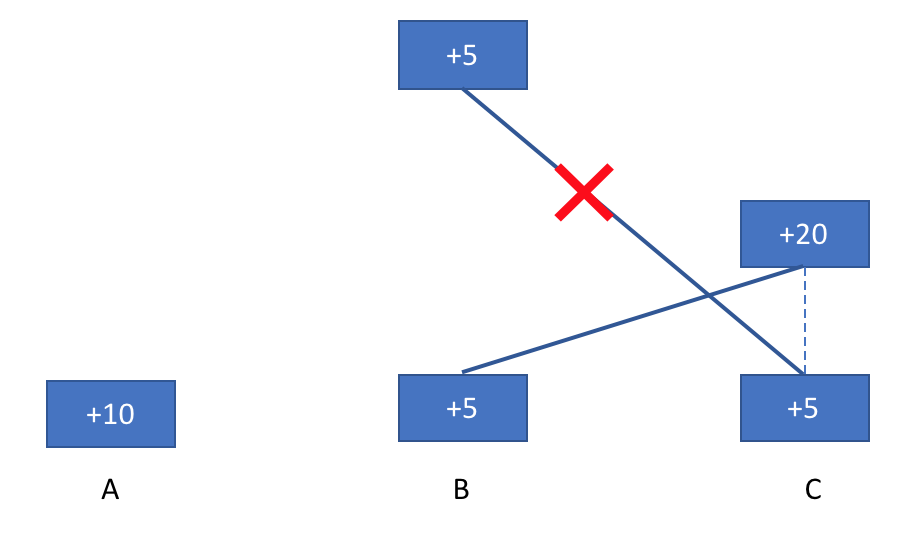
每次新块接入DAG,DAG中estimate safe的块就有可能增加(见前篇图中红色区域),此时要对参与这些块的验证者进行奖励。
注意的是,参与这两步的验证者是不同的。提议只会减少验证者的押金,只有确认才能增加验证者的收入。因此验证者必须轮换做这两步。
现在我们举原文中的例子,见下图,并对原文中的一些概念作解释。

有3个验证者(Validator) A, B, C,产生了块\(b_1, \dots, b_6\),构建了如图所示的DAG。图中带有ack的箭头及其所指向的块是Estimate Safe的,方块中的数字代表押金。\(\mathrm{pca}(b_6) = 3\)表示\(b_6\)的押金。
现在A要接入新的块。不同于之前的押金最大原则,这里采用得分最大原则。DAG中一个块的得分表示为:
\(score(b) = \sum_{b' \in 所有验证者离b最近的块} \quad\quad \quad W(b')\)
其中
\(W(b) = \sum_{\{b' | b \stackrel{\mathbf{ack}}{\rightarrow} b'\}} f\cdot W(b') + \mathrm{pca}(b)\)
代表\(b\)的权重。其中 \(\{b' | b \stackrel{\mathbf{ack}}{\rightarrow} b'\}\)是所有被\(b\)指向的块,箭头带有ack标记。\(f\)是一个参数。
我们可以算一下:\(W(b_6) = 3\),因为\(b_6\)出去的箭头没有ack标记(没有达成共识,不是safe的) \(W(b_5) = f \cdot (W(b_3) + W(b_4)) = f(f \cdot W(b_2) + f \cdot W(b_2)) = 4f^2\)。\(W(b_4) = 2f\)。从而有,
\(score(b_6) = W(b_1) + W(b_5) + W(b_4) = 2+4f^2+2f\)
\(score(b_5) = 4f^2+2f\)
\(score(b_4) = 2f\)
因此\(b_6\)得分最高,所以新块要接入到\(b_6\)。这里可以看到,假如B作弊,假装没看见A和C,则他所连的块就会少,从而得分低,不容易接入新块。
接下来考虑奖励问题。一个块\(b\)变成safe之后,参与验证的每个验证者将获得如下的奖励:
\(\mathrm{pce}(b) = f \left[\sum_{\{b' | b \stackrel{\mathbf{ack}}{\rightarrow} b'\}} \mathrm{pce}(b') + \mathrm{pca}(b)\right]\)
等式右边方括号里的\(\sum_{\{b' | b \stackrel{\mathbf{ack}}{\rightarrow} b'\}} \mathrm{pce}(b') + \mathrm{pca}(b)\) 就是我们之前提到的 PC,奖励的大小正比于PC。
可以看到奖励是递归的,其大小还取决于该块连接的块的奖励,即前一轮的奖励。
2. 使系统稳定的$f$
首先\(f<1\),否则根据pce的递归,奖励将无限放大。
文章Model of Total PC and Quantifying Branching 中提到了一个简单的模型用于测试f对奖励的影响。结论是 \(f\)必须满足 \(a\cdot f \cdot N =1/2\),其中\(a\)为参与acknowledge的验证者的百分比。(1-a)则是参与proposal的验证者百分比。N是总的验证者数。这个结论怎么来的呢?考虑一下下面这个简单的模型。假设\(V_t\)代表\(t\)轮验证者手上的币的总数,\(B_t\)代表\(t\)轮块中所含有的PC(political capital)总和,则\(f B_t\)是每个验证者可以获得的奖励。有
\begin{eqnarray} V_{t+1} & = & a V_t + a f N B_t\nonumber\\ B_{t+1} & = & (1-a) V_t + a f N B_t\nonumber \end{eqnarray}
解释一下:\(t+1\)轮,有\((1-a)\)百分比的验证者参与proposal,因此抵押了\((1-a) V_t\),手上剩下 \(a V_t\)。同时\(a N\)个验证者参与acknowledge,总共获得 \(a f N B_t\)的奖励。因此验证者总共的资产是 \(a V_t + a f N B_t\)。 而块中所含有的PC包含两部分,第一部分是propose的押金\((1-a)V_t\),第二部分则是参与acknowledge验证者所获的的奖励,为什么呢?参考一下前面\(\mathrm{pce}(b)\)的定义,\(\mathrm{pce}(b)=f\)[用ack链接的奖励(即上轮的奖励)+ b的押金].,因此\(t\)所获得的奖励都应该进入\(B_{t+1}\), b的押金总和即\((1-a)V_t\)。
将上述式子写成矩阵的形式,我们会有
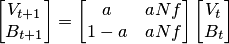
要让系统稳定,即\(B_{t+1} = Bt_t, V_{t+1} = V_t\),则必须其系数矩阵最大特征值为1,由此可以得出\(a f N = 1/2\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号