LCA（最近公共祖先）
什么是最近公共祖先？
来自百度百科的定义：对于有根树T的两个结点u、v，最近公共祖先LCA(T,u,v)表示一个结点x，满足x是u、v的祖先且x的深度尽可能大。
首先让我们给出一个题目【NKOJ2447-最近公共祖先】
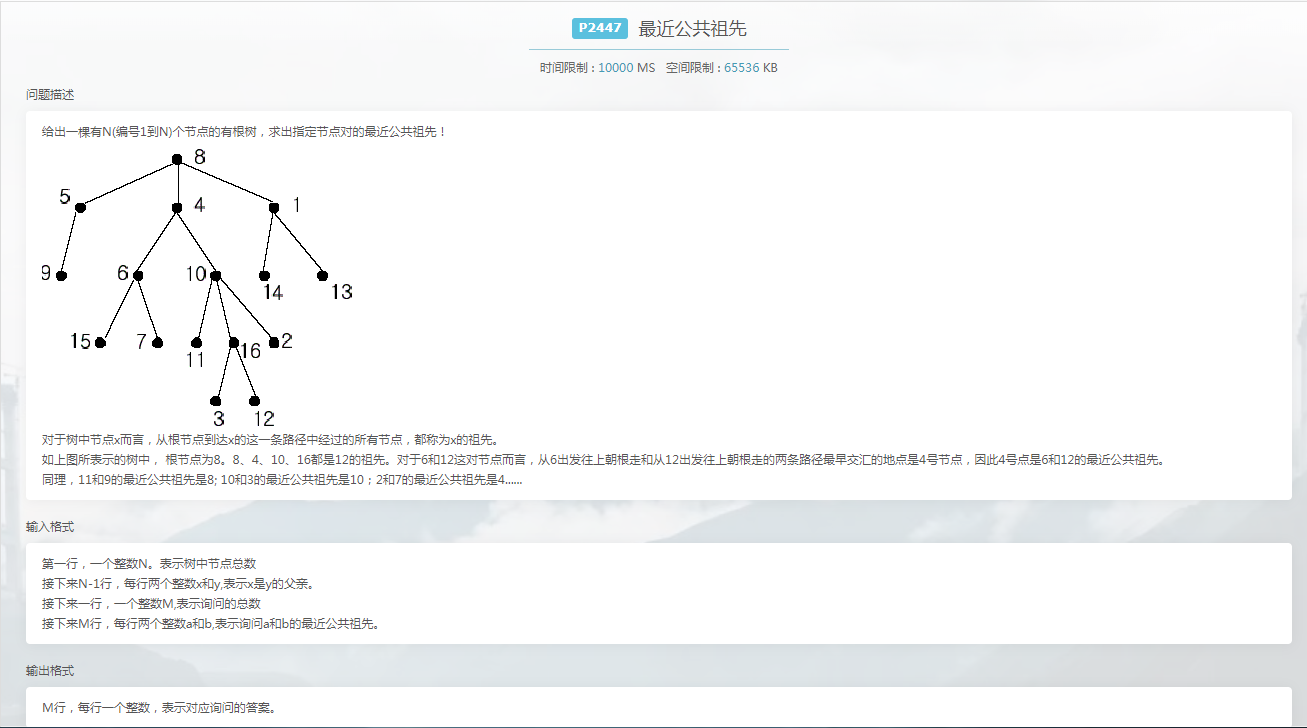
那么我们应该怎样去求最近公共祖先？
我们发现，如果使用暴力枚举第一个点所有的祖先，再看从深度最大的第二个点的祖先去一一验证是否有交集的话，时间复杂度是O（N）的。所以肯定会T。
ORZ。
（不然我们为什么要用LCA）
需要申明的数组
Dep[v]：用于记录节点v的深度；
Fa[v][k]：用于记录节点v向上第\(2^k\)个祖先的编号；
Last[x],End[i],Next[i]：存图；
注：
1.Fa[v][k]中之所以存的是\(2^k\)，是因为在接下来的操作中会使用到位运算；
2.在接下来的操作之中，我们还需要有一个必要的DFS来递归建树；
3.除了Fa[v][k]数组需要预处理以外，其他数组的初值均可赋值为0；
LCA的核心代码讲解
预处理
Fa[v][k] = Fa[Fa[v][k - 1]][k - 1]；
从v号点向上走P层
void Go_Up(int v, int p){
for(int i = 1; i <= s; i ++)//s为倍增上限，注意此处是i < s
if(p & (1 << i) ) v = Fa[v][i];
}
在x与y在同一层后找二者的公共祖先
if(x == y)return x;//假设之前Dep[x] < Dep[y]，那么此情况则相当于之前x是y的子孙
int s = ceil(log2(Dep[x]));//向上倍增的上限
for(int i = s; i >= 0; i --){
if(Fa[x][i] != Fa[y][i]){
x = Fa[x][i];
y = Fa[x][i];
}
}
return Fa[x][0];
在这里，有几个思考的问题：
1.为什么i层的循环是从s到1？
2.为什么祖先相同的时候不向上走，祖先不同的时候反而向上走？
3.最后的结果是什么？
对于第1，2个问题，我们来作这样的一个假设：
假设x是u和v的最近公共祖先，那么会有这样的两条结论
* x往上到根的路径上的所有点都是u和v的公共祖先；
所以当fa[u][i]==fa[v][i]条件成立时，fa[u][i]不一定是它们的最近公共祖先。
* 若fa[u][i]!=fa[v][i],说明点fa[u][i]和点fa[v][i]一定是x下方的点
由此，我们不难看出，1，2这两种措施都是为了防止“跳过头”，以免所求仅满足了“公共祖先”而未满足“最近”
所以说第3个问题的答案也就出来了。x，y停下来的位置再向上数一层既是所求的最近公共祖先
到这里，我们就讲解完了LAC的核心代码，接下来，我将给出LCA代码的模版（也就是在一开始我给出的例题的完整代码，我将会在其中以注释的方式进一步阐述说明）
建议先看LCA函数，再看主函数，最后看DFS函数
LCA代码模版
#include <stdio.h>
#include <bits/stdc++.h>
using namespace std;
int n, m, x, y;
int End[10005], Next[10005], Last[10005], Dep[10005],Fa[10005][20];
void DFS(int x){
Dep[x] = Dep[Fa[x][0]] + 1;
//由于在DFS中，我们是由根节点从上往下讨论的，所以我们可以保证x的father已经被算了出来
int s = ceil(log2(Dep[x]));
//计算倍增上限,ceil向上取整
for(int i = 1; i <= s; i ++)
Fa[x][i] = Fa[Fa[x][i - 1]][i - 1];
////倍增计算祖先 【核心代码1】
for(int i=Last[x];i;i=Next[i])
if(End[i]!=Fa[x][0])Fa[End[i]][0]=x,DFS(End[i]);
}
int LCA(int x, int y){
int i, k, s;
s = ceil(log2(n));//计算倍增上限
if(Dep[x] < Dep[y])swap(x, y);//保证x在y的下方，交换无影响
k = Dep[x] - Dep[y];
for(int i = 0 ; i <= s; i ++)
if(k & (1 << i))x = Fa[x][i];//GO_UP 【核心代码2】
if(x == y)return x;//如果x == y，则说明x之前是y的子孙，那么x，y的最近公共祖先就是y（也就是现在的x）
s = ceil(log2(Dep[x]));
for(int i = s; i >= 0; i --)//【核心代码3】
if(Fa[x][i] != Fa[y][i]){
x = Fa[x][i];
y = Fa[y][i];
}
return Fa[x][0];//此时Fa[x][0]（x节点向上数一层）就是x，y的最近公共祖先
}
int main(){
scanf("%d", &n);
for(int i = 1; i < n ; i ++){
scanf("%d%d", &x, &y);
Fa[y][0] = x;//记下y的father
End[i] = y;
Next[i] = Last[x];
Last[x] = i;
}
for(int i = 1; i <= n; i ++){
if(Fa[i][0] == 0){// 2^0 == 1，所以Fa[i][0]就记的是该节点的父亲
DFS(i);
break;
}
}
//由于这是一棵树，所以说这一步代码的目的就在于找出没有父亲的孤儿节点——即根节点root
//DFS的目的即初始化Fa[v][k]数组
scanf("%d", &m);
for(int i = 1; i <= m; i ++){
scanf("%d%d", &x, &y);
printf("%d\n", LCA(x, y));
}
return 0;
}
LCA大概就是这样orz，由于我太菜了所以说可能会有表述不清楚的地方，所以如果有没有理解到的地方欢迎骚扰什么的orz
