Treap 学习笔记
一、Treap
Treap 是一种通过旋转操作维护性质的二叉搜索树。
定义详见
要维护的东西还是一样，对于每个节点，要维护它的左右儿子，子树大小，还有权值和随机的优先级（这样才能保证树的高度是 \(O(\log n)\) 级别的）。
注意：旋转、分裂、伸展什么的都是手段，维持平衡树的 2 个性质才是目的。
对于全局，要维护树根的编号和当前有多少个节点。
二、实现
1. 旋转
由于插入、删除操作需要维护二叉搜索树的性质，所以我们需要一个操作来调整 Treap。它的核心操作就是旋转。
旋转的目标是在整棵树的中序遍历不变的情况下改变父子关系，让优先级小的节点更浅。而中序遍历递增可以在插入、删除操作中维护。
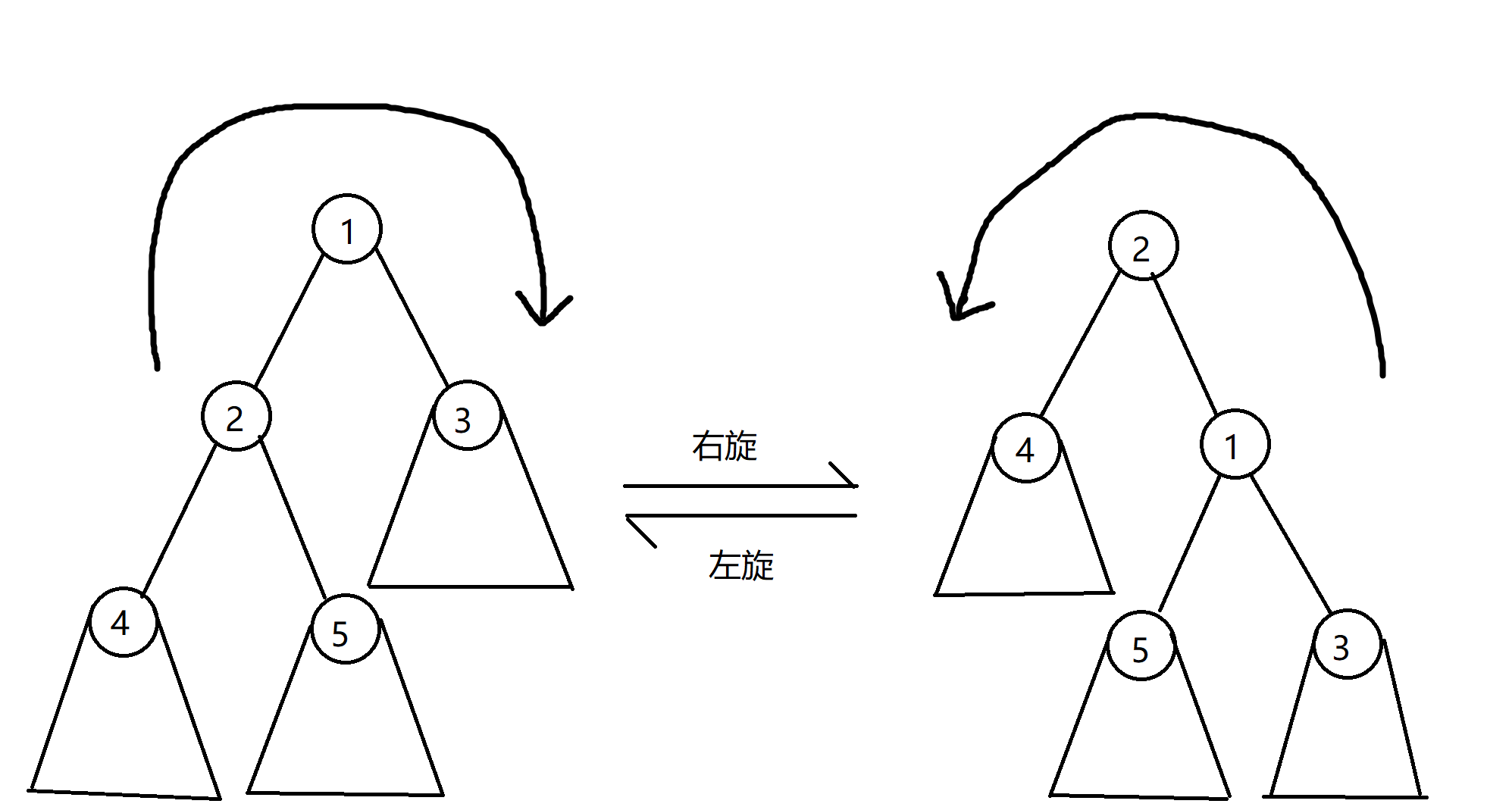
我们惊喜地看到，全树中序遍历没有变（都是 4 的子树->2->5 的子树->1->3 的子树），并且有且仅有 1、2 父子关系改变了。
然后来讲一下旋转操作具体怎么做。先放代码。
1. 维护操作
维护一个节点的子树大小，就是它自己加上左右子树的大小。
void upd(int x){
t[x].s=t[t[x].l].s+t[t[x].r].s+1;
}
时间复杂度 \(O(1)\)。
2. 右旋
inline void rrot(int &x){
int y=t[x].l;
t[x].l=t[y].r;
t[y].r=x;
upd(x);
upd(y);
x=y;
}
大概就是这样（绿色的节点表示维护完成）：
- 记录 \(y\) 为 \(x\) 的左子节点。
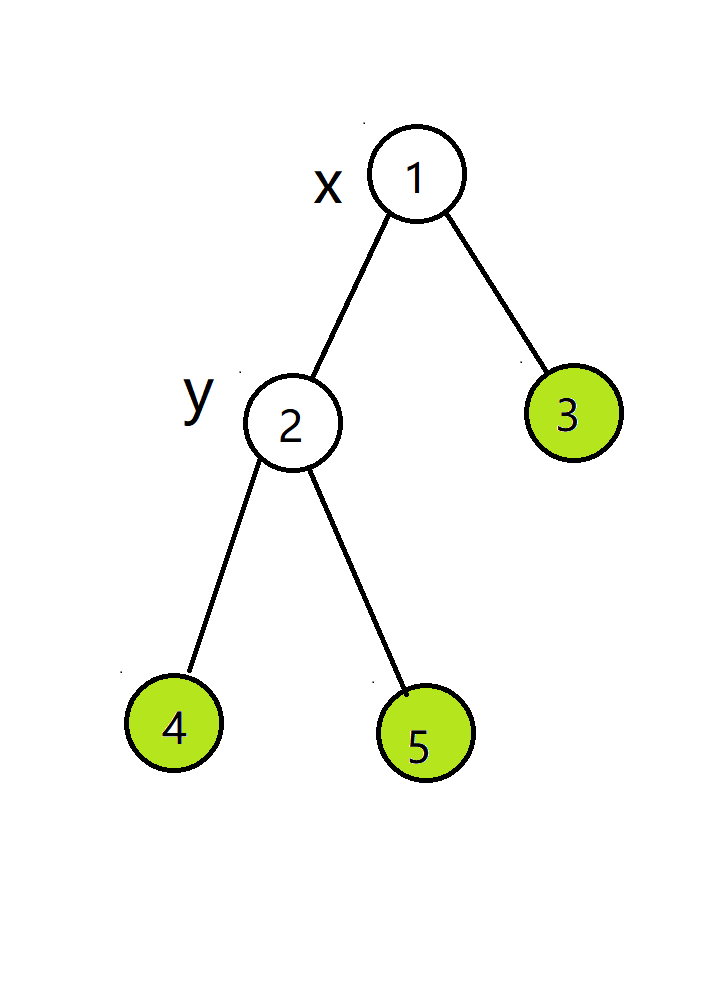
- 令 \(x\) 的左节点变为 \(y\) 的右节点。
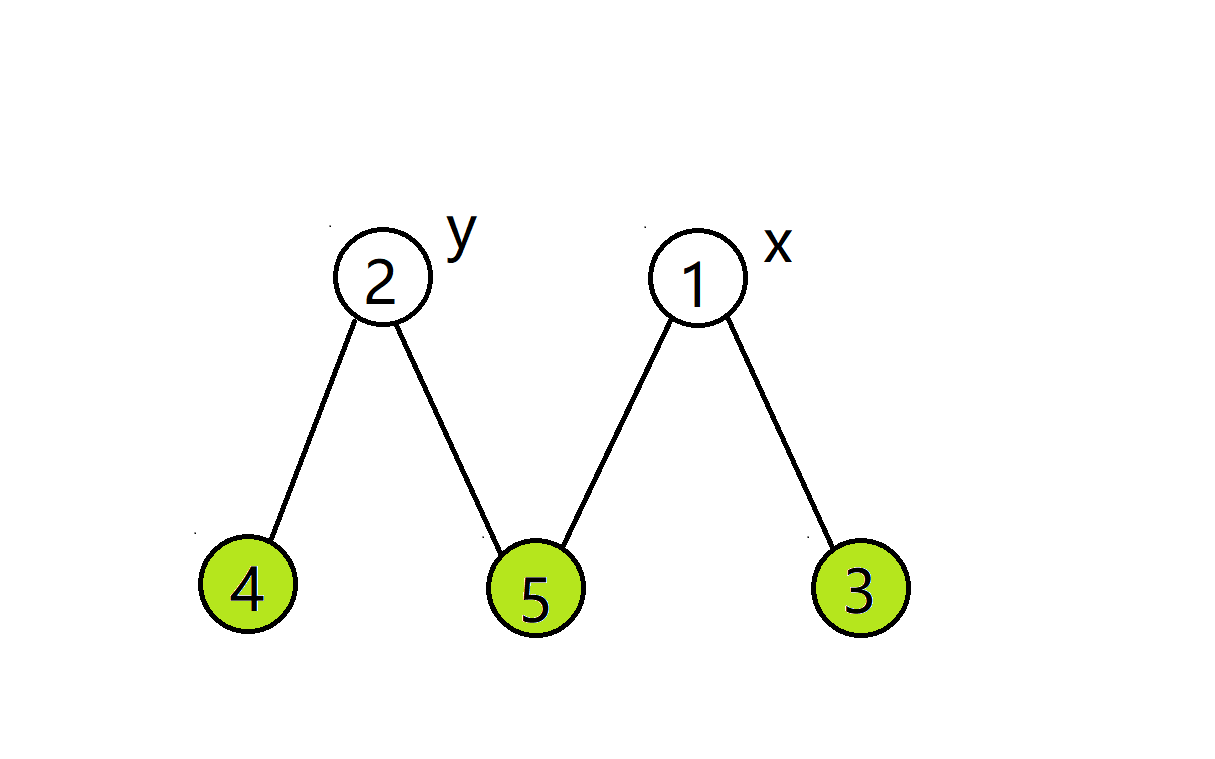
- 令 \(y\) 的右节点变为 \(x\)。
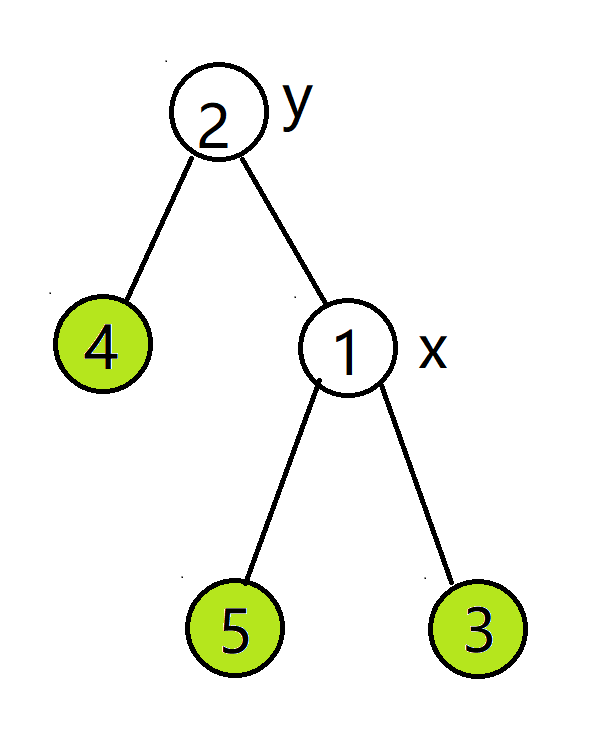
- 维护 \(x\)，再维护 \(y\)（顺序不能乱）
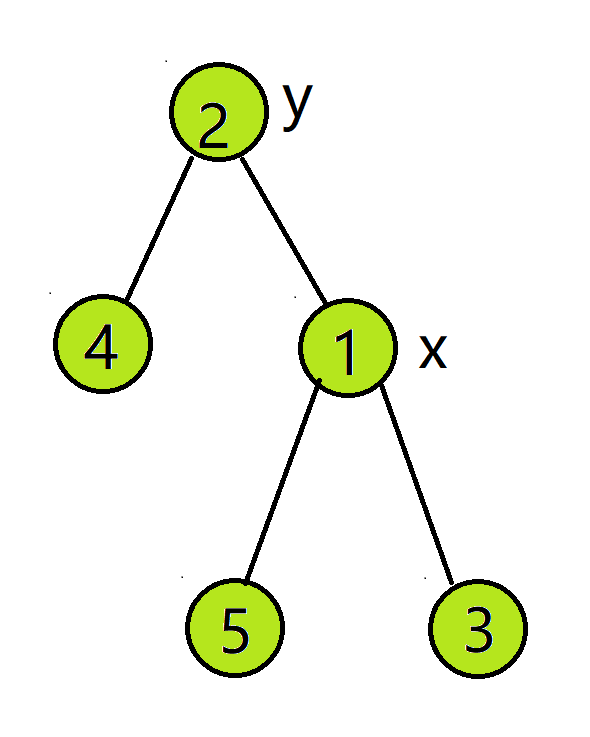
- 令根节点为 \(y\)。
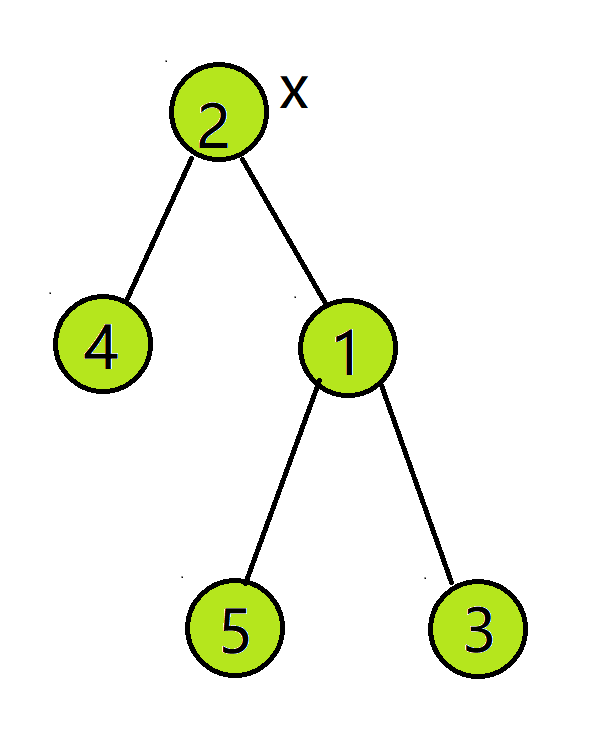
时间复杂度 \(O(1)\)。
3. 左旋
我们发现，右旋和左旋互为逆运算，而且左右对称，所以我们把右旋的所有左右反过来就行啦。
inline void lrot(int &x){
int y=t[x].r;
t[x].r=t[y].l;
t[y].l=x;
upd(x);
upd(y);
x=y;
}
时间复杂度 \(O(1)\)。
4. 插入
要插入一个数，而且要保证二叉搜索树性质，所以我们递归：
-
判断要插入的数与当前节点的关系。如果小于等于，插入到左子树。否则插入到右子树。
-
如果遇到一个空节点，就新增一个节点并返回。
-
然后回溯时要维护堆性质。那么我们往哪个方向插入了新数字，那个方向的堆性质才会被破坏。所以判断一下那个方向的堆性质有没有被破坏，如果有，进行对应的旋转即可。
inline void ins(int &x,int v){
if(!x){
t[x=++c]={0,0,1,v,rand()};
return;
}
t[x].s++;
if(v<=t[x].v){
ins(t[x].l,v);
if(t[t[x].l].p<t[x].p)rrot(x);
}else{
ins(t[x].r,v);
if(t[t[x].r].p<t[x].p)lrot(x);
}
}
时间复杂度 \(O(树高)\)，也就是 \(O(\log n)\)。当然实际上跑不满，因为一旦回溯到某一个地方时，发现不用旋转也满足了堆性质，那么这个地方及以上都不用旋转了。
5. 删除
要删除一个数，采用二叉堆的思想，将一个数旋转到叶子节点再删除。由于旋转操作不改变二叉搜索树性质，所以我们要维护堆性质：一个数的优先级小于等于它的儿子。那我们在将一个数向下旋转的时候，肯定是选择一个优先级小的转上来。
inline void del(int &x,int v){
if(t[x].v==v){
if(!t[x].l||!t[x].r){
x=t[x].l+t[x].r;
return;
}
if(t[t[x].l].p>t[t[x].r].p){
lrot(x);
del(t[x].l,v);
}else{
rrot(x);
del(t[x].r,v);
}
}else if(t[x].v>v)del(t[x].l,v);
else del(t[x].r,v);
upd(x);
}
时间复杂度 \(O(\log n)\)。
6. 查询 x 数的排名
照样是分左右子树查询。
注意一定要查询到空节点为止。
inline int vtr(int x,int v){
if(!x)return 1;
if(t[x].v>=v)return vtr(t[x].l,v);
return vtr(t[x].r,v)+t[t[x].l].s+1;
}
时间复杂度 \(O(\log n)\)。
7. 查询排名为 x 的数
inline int rtv(int x,int v){
if(t[t[x].l].s==v-1)return t[x].v;
if(t[t[x].l].s>=v)return rtv(t[x].l,v);
return rtv(t[x].r,v-1-t[t[x].l].s);
}
时间复杂度 \(O(\log n)\)。
8. 查询前驱
inline int pre(int x,int v){
if(!x)return -I;
if(t[x].v>=v)return pre(t[x].l,v);
return max(t[x].v,pre(t[x].r,v));
}
时间复杂度 \(O(\log n)\)。
9. 查询后缀
inline int nxt(int x,int v){
if(!x)return I;
if(t[x].v<=v)return nxt(t[x].r,v);
return min(t[x].v,nxt(t[x].l,v));
}
时间复杂度 \(O(\log n)\)。
