堆与二叉搜索树学习笔记
部分内容来自 OI-WIKI。
1. 堆
0. 堆的定义
堆是一棵二叉树，满足每个节点的键值都大于等于它的父亲节点或者小于等于它的父亲节点。每个节点的键值都大于等于它的父亲节点的叫小根堆，每个节点的键值都小于等于它的父亲节点的叫大根堆。
优先队列是一种抽象数据类型，它是一种容器，里面有一些元素，这些元素也称为队列中的节点。优先队列的节点至少要包含一种性质：有序性，也就是说任意两个节点可以比较大小。为了具体起见我们假设这些节点中都包含一个键值，节点的大小通过比较它们的键值而定。优先队列有三个基本的操作：插入节点，取得最小/大节点和删除最小/大节点。
常见的优先队列是二叉堆。
可并堆代表一种抽象数据结构，不仅能支持以上三种操作，还支持将两个堆合为一个的操作。但是两个二叉堆合并的时间复杂度是 \(O(n)\) 的，十分不优秀。所以存在配对堆、二项堆、左偏树等可以在 \(O(\log n)\) 甚至 \(O(1)\) 的时间复杂度内进行堆的合并。
单次操作时间复杂度：
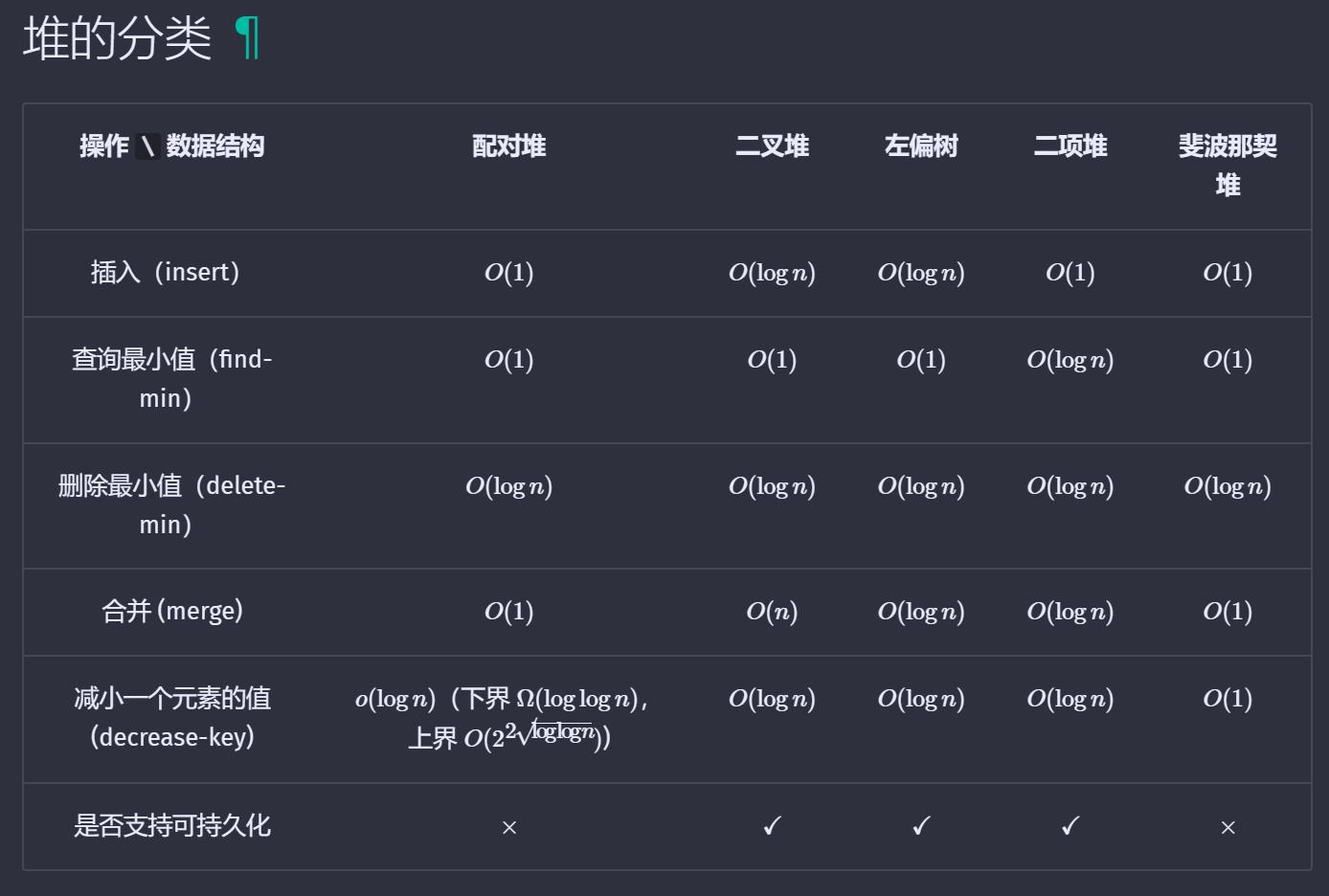
1. 二叉堆
2. 配对堆
3. 左偏树
2. 二叉搜索树
0. 二叉搜索树的定义与性质
- 首先，这是一棵二叉树，它的最主要的性质就是中序遍历单调不减，即对于每一个节点，它的权值小于等于它的右儿子，大于等于它的左儿子。但是我们发现，如果我们要将一个单调不降的数列插入二叉搜索树，那就会导致每次插入在最底端，二叉搜索树退化成链，时间复杂度变为 \(O(n^2)\)。
- 平衡树：
首先平衡树有三个性质：
-
堆性质，这里我们将维护一个小根堆（事实上维护大根堆也没有关系），即是一棵二叉树，树中每个节点的优先级值都会大于它的左儿子和右儿子。
-
搜索树性质，也就是每个节点的权值大于等于它左儿子的权值（如果有的话），并且小于等于它右儿子的权值（如果有的话）。更进一步，每个节点的权值大于等于它左子树所有节点的最大权值，小于等于它右子树所有节点的最小权值。
-
深度为 \(\log n\) 左右。
那么我们怎么维护它呢？
我们用一个结构体来维护平衡树每个节点的信息。
struct bst{
int l,r;//左右儿子
int pri,val;//优先级和权值
int sz;//以它为根的子树大小
}t[100010];
当然不同题目不同对待。
然后就是当前树根的编号 \(rt\)，以及当前新节点的编号 \(cnt\)，设为全局变量。
