CF1887E

题面

Alice 和你玩游戏。有一个 \(n\times n\) 的网格，初始时没有颜色。Alice 在游戏开始前依次给其中 \(2n\) 个格子分别涂上了第 \(1\sim 2n\) 种颜色，并告诉你每个颜色的位置。

接下来的每次操作，你可以选择一个未涂色的格子，由 Alice 在 \(2n\) 种颜色中选择一个涂在该格子上，并告诉你该颜色。

如果在某次操作后方格图上存在四个不同颜色的点，且它们的位置形成一个平行于边线的矩形，则输出它们以获得胜利。

你至多进行 \(10\) 次操作，请构造一个获胜方案。交互库自适应，也就是说 Alice 的决策与你的选择有关。

\(T\le200,n\le 1000\)。

题解

很有意思的一道题，告诉了我们如果在原题面摸索没有头绪，那么就要找到一个可以与题面对应上的模型。

像在此题中，就可以把网格对应到二分图中。这样：

• 第 \(i\) 行 \(j\) 列颜色为 \(c\) 的格子 \(\to\) 第 \(i\) 个点连了 \(j+n\) 个点权值为 \(c\) 的边。
• 四个不同颜色的平行于边线的矩形的点 \(\to\) 权值不同的四元环

并且题目保证最开始就有 \(2n\) 条权值不同的边，所以此时图中一定有权值不同的环。

我们对这样的一个环去分析。（蒯来的图）

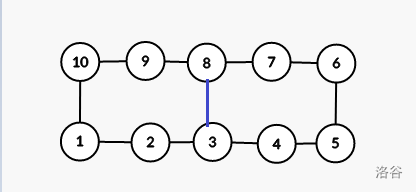
我们在环的中间连上一条边，然后可以注意到，无论Alice给他涂上什么颜色，左右边两个环中一定有一个环的边权是互不相同的。

这样就会是环的大小减少一半，最终满足要求。

启发

• 把陌生的问题对应到一个熟悉的模型上。