树分治
点/边分治
关于点分治和边分治,个人感觉就是将序列上的分治问题转化为了树上的分治问题,为了每次让划分的子问题更平均,所以才有了点分治的找重心、边分治的边三度化。剩下的部分基本都可以看出序列分治的影子。
点分治
想想序列的分治是怎么样的?找中点,处理跨过中点的贡献,之后在递归处理两边的子问题,既然说点分治就是树上的序列分治,那么同样的,我们找到重心,然后处理跨过重心的路径,然后递归处理子问题。
大致模板是这样的:
void sous2(int x){
chuli(x);//处理答案
v[x]=1;//划定边界,无论是处理答案还是寻找重心都不能经过。
for(int i=h[x];i;i=a[i].ne){
int y=a[i].y;
if(v[y])continue;
masi=1e9;
sous1(y,x,si[y]);//找重心
sous2(root);//递归处理子问题
}
}
但上面的这个有一点小问题,就是在找重心直接引入si[y],但只会带来常数上的影响,不会有大问题。详见
接下来就是处理答案的地方了,因为我们不能将同一棵子树内的点互相贡献,所以问题可能就会变成:进行多次加入操作,进行多次询问操作,再多次加入...可以看出,这是一个动态问题。
但是你也可以记录每一个点来自哪个子树,然后离线,离线的时候排除来自同样子树的情况就可以,只不过这个排除同子树的离线操作使用问题很少,所以一般不会采用。
void chuli(int x){
for(int i=h[x];i;i=a[i].ne){
int y=a[i].y;
if(v[y])continue;
top=0;
sous3(y,x);//将y这棵子树的节点都存入b中
for(int i=pr;i<=top;++i)这里是查询
for(int i=pr;i<=top;++i)这里是修改
}
这里是删除/撤回修改
当然也可以都存在一起之后离线排序。
}
接下来就是具体例子。
-
\(m\le 100\)次询问树上\(n\le 10^4\)距离为 \(k\) 的点对是否存在。
这里的多次询问貌似只是防随机数过题的情况...所以我们就将其当做单次询问。
在线处理的话可以根据值域大小选用桶或者
unordered_map。当然,这也是为数不多的可以离线处理的题,我们可以排序之后用指针做,由于只需要判断可行性,可以快速排除同子树情况。
-
P7565 [JOISC 2021 Day3] ビーバーの会合 2
给定一棵有 \(N\) 个点的树,每一个点上有一个人,这些人要开会,假设一次会议有 \(P\) 个人参加,这 第\(i\) 个人在第 \(p_i\) 个点上。如果点 \(k\in[1,n]\) 满足下面这个值最小。
\[\sum\limits_{i=1}^Pdis(k,p_i) \]那么就称第 \(k\) 个点为可期待的,这场会议的期待值即为所有点中中可期待点的个数。
对于每个 \(j \in [1,N]\),求当会议里有 \(j\) 个人的时候,会议的期待值的最大值是多少。
分析一下,我们需要对每一个\(j\),求最长的链的长度,使两端链底各带有\(j\)个节点。链的长度就是\(2\times j\)的答案。
看起来,我们在递归子树的时候无法忽视在当前处理问题外的节点(也就是当前子树外的节点),但实际上,由于重心的性质(子树大小不会超过整树的一半),一旦有节点要以处理完的重心作为链底的节点,那么这条链链底的节点大小将超过当前树大小的一半,肯定不会对答案产生贡献。
那么我们就可以忽略这些被处理过的点,所以和正常的点分治没有区别了。
现在再来考虑处理答案,开一个桶,维护当前某一链底大小为 \(i\) 的链到当前根的最大长度,这个可以直接在
sous3的时候更新单点,之后维护后缀和处理答案就行。注意单链也可以作为答案,就是某一链底为根的情况,这时候由于重心的性质,一定是满足条件的。
-
给定一棵由 \(n(\le 2\times10^5)\) 个点构成以 \(1\) 为根的树,对于 \(v\neq 1\),它父亲是 \(f_v\) ,到父亲的距离为 \(s_v\)。
对于 \(v\) 的一个祖先 \(A\) ,只有它们距离不超过 \(l_v\) 时,v 才可以直接到达城市\(A\),代价为 \(dis(A, v)p_v + q_v\) 。否则不能直接到达。对于每个节点求出到达根节点的最少代价。记得用cdq维护dp的情况吗?先递归左边,再处理当前,最后递归右边还记得为什么吗?
记得那就好办了,树上也是一样的。对于当前分治中心 \(x\) ,我们先去递归处理 \(x\) 的父亲部分,再将当前上界(这里的上界就类似序列中的区间限制)内的点都当做修改,之后遍历其他的子树作为询问。因为修改询问分开,可以离线处理 \(l\) 的限制。
具体来说,可以将点按\(dep_v-l_v\)排序,这样可以用指针维护加入的修改,因为加入的修改 \(x\) 有序,查询是无序,可以插入时单调栈,查询时二分。
细节:因为加入修改的 \(x\) 为降序,所以斜率的处理会有一些不同。
大概就是这些内容,点分治和序列的分治真的很像(尤其是这个dp,简直一模一样)。
注意一点:一旦点分治的分治重心或边界处理出问题了,普通数据是无法检验出来的,所以一定要测极限数据,最好是链、菊花等强力数据。
边分治
内容其实和点分治差不多,每次选择一个边作为分治中心,即对于一条边 \(i\) ,处理经过边 \(i\) 的路径。
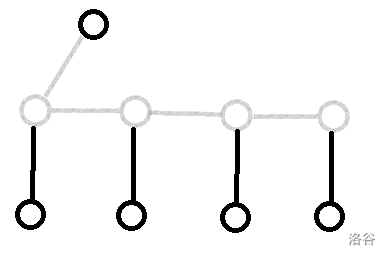
这样处理的好处就是只会有两端经过这个分治的边。这样我们就可以省去在点分治的时候烦人的排除子树内答案的操作。
但是这样会被菊花图卡掉,所以需要边三度化。边三度化的方法有很多,这里使用将所有儿子依次加一个点串起来的方法,如图:
代码:
int top,la[maxn];
void add1(int x,int y,int z){
if(si[x]<si[y])swap(x,y);//这里的目的是让x为y的父亲。
if(!la[x]){
la[x]=x;
T1.add(la[x],y,z);T1.add(y,la[x],z);
}
else{
++top;
T1.add(la[x],top,0),T1.add(top,la[x],0);
la[x]=top;
T1.add(top,y,z),T1.add(y,top,z);
}
}
之后找边均分怎么办?其实就可以通过找重心来均分,因为边可以对应点。代码是这样的:
void sous1(int x,int fa,int S,int id){
si[x]=1;
int ma=0;
for(int i=T1.h[x];i;i=T1.a[i].ne){
int y=T1.a[i].y;
if(!y||y==fa)continue;
sous1(y,x,S,i);
si[x]+=si[y];
ma=max(ma,si[y]);
}
ma=max(ma,S-si[x]);
if(id&&ma<misi)misi=ma,root=id;
}
看起来好像和点分治没有什么差别,确实是这样的。找到这条边之后,我们将这个边和反边的 \(y\) 都赋为 \(0\) ,这样就是消除了这个边。
之后的出来就和点分治大同小异了。
-
给两棵树 \(T1,T2\) ,求\(\max_{x,y}\{\text{depth}(x)+\text{depth}(y)-\text{depth}(lca_{x,y})-\text{depth}'(lca'_{x,y})\}\)
考虑化一下式子,得到\(\frac{1}{2}(\text{depth}(x)+\text{depth}(y)+dis(x,y))-\text{depth}'(lca'_{x,y})\)。
我们先考虑点分治,对于分治中心,我们遍历其子树,设\(val_x=\text{depth}(x)+\text{距离分治重心的距离}\),答案就是\(\frac{1}{2}(val_x+val_y)-\text{depth}'(lca'_{x,y})\)。
我们可以对这些遍历到的点在\(T2\)上建一虚树,对于虚树上的点 \(x\) 考虑以 \(x\) 为lca时的答案,但是这样对于多个子树的点我们无法排除,只能用边分治,这样在只有两边的点之后我们就可以用\(g_{x,0/1}\)来排除同树的情况了。
点分树
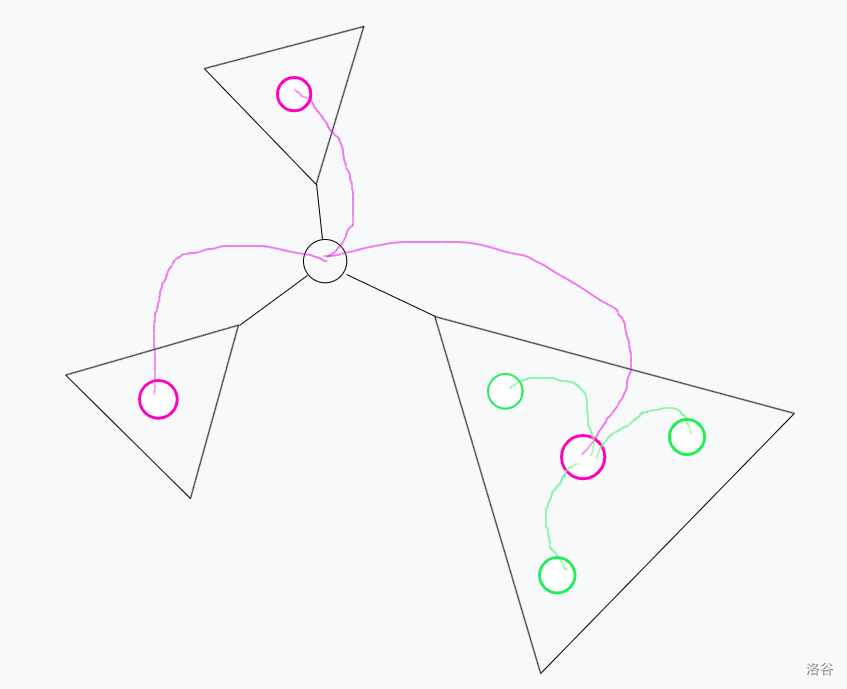
做完点/边分治的题目之后,你可能会注意到如果一道题目可以点/边分治,最重要的一点就是题目允许离线,并且没有修改。那么,如果题目需要我们支持这些操作怎么办?这个时候点分树就来了。
ps:为什么没有边分树...emm....只是没有相关的题目罢了。
点分树的思想很简单,就是将普通点分治的划分过程提前处理,并且将在每次分治的时候让各个子树的分治中心连接到当前中心上,如图:
代码长这样:
vector<int> b[maxn];
int fa2[maxn],top[maxn];
void sous2(int x){
v[x]=1;
for(int i=h[x];i;i=a[i].ne){
int y=a[i].y;
if(v[y])continue;
misi=1e9;
sous1(y,x,si[y]);//正常在y子树内找重心
fa2[root]=x,b[x].push_back(root);
//根据情况确定是否需要保留父亲和儿子的访问
sous3(y,x);//如果初始有信息可以先获取一遍。
sous2(root);
}
}
这样的操作之后,有几个性质:
-
这棵树的高度是 \(O(\log n)\) 的。这表明,我们可以暴力跳点分树的父亲来得到信息或更新。
-
任意两个点 \(x,y\) 的点分树上的
LCA一定在原树两点的简单路径上。而且在 \(x,y\) 的公共祖先中,LCA是唯一满足这个性质的。这表明,如果我们需要得到关于\(\text{path}_{x,y}\)的信息,只需要在点分树上的LCA位置存储。
其实你也可以理解为我提前得到了点分治过程中需要暴力遍历整棵树的信息,这样就之需要递归 \(\log n\) 次就可以得到答案。同样的,由于一个点 \(x\) 的信息只会被存储到 \(x\) 点分树的祖先上,但这样的祖先只有 \(\log n\) 个,所以我们也可以暴力修改。
注意一点,就是我们点分治的时候必须要排除位于同一棵子树的贡献,所以在点分树上。我们一般会用两个数组、数据结构 \(f,g\) 来维护答案,意义如下:
- \(f_x:\) 表示点分树中 \(x\) 子树的所有点在 \(x\) 处产生的贡献。
- \(g_x :\) 表示点分树中 \(x\) 子树的所有点在 \(fa_x\) 出产生的贡献。
这样,一旦贡献满足可删性,我们就可以在遍历的过程中加上 \(f_x\) 的贡献,减去 \(g_x\) 的贡献。
void change1(int x,int y){
int now=x;
change to f[x]
while(fa2[now]){
change to g[now]
now=fa2[now];
change to f[now]
}
}
void query(int x){
int now=x,ans=f[x].ans;
while(fa2[now]){
ans-=g[now].ans;
now=fa2[now];
ans+=f[now].ans;
}
}
当然往往我们不能只用这\(f,g\)就能得到答案,这就需要哦具体问题具体分析了。
-
一棵树,点有点权、边权为 1,多次操作。每次操作要么修改一个点权,要么询问到 \(u\) 的距离不超过 \(p\) 的点的点权和。强制在线
先考虑用点分治处理只有一次询问怎么办?对于一个分治重心 \(now\) ,先求出与 \(u\) 的距离 \(dis\) 。然后需要找距离分治重心 \(\le p-dis\) 的点的点权和。注意需要排除掉 \(u\) 子树内的点,并且往这棵子树内递归。
现在点分树可以帮我们找到需要的分治重心,现在考虑怎么维护信息。
先不考虑修改,我们设 \(f_{x,i}\) 表示点分树中 \(x\) 子树中距离 \(x\) 小于等于 \(i\) 的点的点权, \(g_{x,i}\) 表示点分树中 \(x\) 子树中距离 \(fa_x\) 小于等于 \(i\) 的点的点权,这样我们就可以查询 \(f_{x,p-dis}\) 得到答案,因为点分治保证了点数的限制,所以整体的空间复杂度是 \(O(n\log n)\) 的。
然而还有修改,那么有什么东西可以支持单点修改,前缀查询呢——树状数组!把数组改成树状数组就行了。
-
给定一棵树,边带负权,求点集最长直径,支持对点集插入和删除。
同样考虑如何点分治处理,对于一个分治重心,我们需要对每个子树找到在该子树中且位于点集中距离分治重心最远的点,然后对于每个分治重心求前两个最远的拼成一条路径。
那么现在考虑点分树怎么维护这些值。
发现原来的容斥思想设 \(f,g\) 无法适用。观察求点分治的过程,我们不妨用 \(g_x\) 表示 \(x\) 子树中所有在点集中的点与 \(fa_x\) 的距离,\(f_x\) 表示各个子树最远的距离,更新时选 \(g_x\) 的最大值加入\(f_{fa_x}\)中,答案就是所有 \(f_x\) 内的最大值和次大值和的最大值。
要支持加入和删除,就用可删堆维护。
点分树差不多就是这样,可以发现,点分树就是点分治的在线化算法,每次点分树查询、修改所涉及的信息必须是单点,难点就是维护 \(f,g\) 而且通过上面的题你也知道 \(f,g\) 并不只是数组,也可以是数据结构。



