排列组合&容斥

排列组合

• 排列组合的题目，一般看起来都很复杂，但都可以拆分成一个个最基本的小问题，再通过加法原理＆乘法原理合并。

• 当然，如果有时候正向拆分很困难，可以试试反向拆，即所有情况－不满足的情况（这种容斥思想会在下面详细说明）

• 分析小问题时弄清楚条件：是不是小球放进盒子的类型？有没有编号？可不可以有空盒？...

• 小练手：

  • 问题一：

    一副$n$种取值，$m$种花色的扑克，从中选5张，求两对同值的方案数

    • 先考虑同值的是哪两种值，共$C_n^2$种方案

    • 而对于每一种取值取两张，都有$C_m^2$种方案

    • 最后一张牌，要与前面的两种取值不同，就是$(n-2)m$方案，

    • 相乘即可。

  • 问题二：

    有$n$个男生，$m$个女生，$2$名老师排队，求满足条件的方案数

    １.两个女生不能相邻

    2.老师也不能相邻

    • 方法一：

      • 思考：因为老师不能相邻，所以他们之间一定夹了学生，又因为女生不能相邻，所以老师之间要么夹了一个女生，要么夹了一个男生和其它学生（也可以没有其它学生）
      • 如果两老师中间夹了一个女生：把这三个人当１个男生，问题转化为：$n+1$个男生中插$m-1$个女生的方案数乘上$2\times m$，即$C_{n+1+1}^{m-1}\times (n+1)!\times (m-1)!\times 2$。
      • 两老师之间夹了一个男生和其它学生：考虑先在$n$个男生中差两个老师，然后再在这$n+2$个人中插$m$个女生，答案为$n!\times C_{n+1}^2\times 2\times C_{n+3}^m\times m!$
      • 最后相加。

    • 方法二：

      • 满足条件的方案＝满足条件１的所有方案－满足条件１且不满足条件2的方案。
      • 满足条件１的所有方案：将老师看作２个男生，问题转化为“$n+2$个男生中插$m$个女生的方案数”，即$C_{n+2+1}^m\times (n+2)!\times m!$。
      • 满足条件１且不满足条件2的方案：将老师绑在一起（绑法有两种），看作１个男生，问题转化为“$n+1$个男生中插$m$个女生的方案数乘上２”，即$C_{n+1+1}^m\times (n+1)!\times m!\times2$。
      • 最后相减。

• 组合意义
  通过对问题组合意义的分析，可以快速对复杂问题化简，不过还是得注意细节，不然很容易出错。

  • 问题一：

    从$(0,0)$只能向上或向右走到$(n,m)$的方案数。

    • 其实就是对$n+m$步决策向上或右中选$n$个向上或$m$个向右，所以答案为$C_{n+m}^n$或$C_{n+m}^m$。

  • 问题二：

    证明$C_{n+r+1}^r=\sum_{i=0}^rC_{n+i}^i$

    • 先将$C_{n}^m$转化为走路问题，原式就转化为"从$(0,0)$走到$(n+1,r)$的方案数"=$\sum_{i=0}^n$从$(0,0)$走到$(n,i)$的方案数
    • 而从$(0,0)$走到$(n+1,r)$可以转化为从$(0,0)$到达$(n,i)\;\;i\in [0,r]$之后向右一步，然后一直向上。所以就是上面式子所表达的。

  • 问题三：

    允许重复的组合：从$A=\{1,2...n\}$中选$r$个元素$\{a_1,a_2...a_r\}$，并且允许重复选取一个元素多次的方案数。

    • 把问题转化为：把这$r$个元素进行划分，分成$n$个部分（可以为空），$\{a_1...a_j|a_{j+1}...a_k|\;\;|a_{k+1}...a_r\}$。并且把分成的$n$段分别是集合$A$中的第$i$个元素，如果这一段是空的就表示没有选第$i$个元素（因为集合并不要求）。
    • 发现如果$n$个部分都不能为空，那就可以运用插板法，在$r$个元素的$r-1$个空格之间选$n-1$个插上隔板，作为分组的端点。
    • 而因为分组可以为空，我们可以先加入$n$个额外的元素，参与插板。这样，在最后分好的$n$个部分每个都减1个元素。这样就可以转化为可以为空的插板问题。
    • 所以答案为$C_{n+r-1}^{n-1}$

  • 问题四：

    有$n$个元素的集合$S=\{0,1,...n\}$和整数$k$，从$S$中选取$\frac{k\times (k+1) }{2}$个子集，构成一个边长为$k$的三角形：

    $A_{1,1}$

    $A_{2,1},A_{2,2}$

    $A_{3,1},A_{3,2},A_{3,3}$

    ......

    $A_{k,1},A_{k,2},A_{k,3}......A_{k,k}$
    要求满足$A_{i,j} \subseteq A_{i,j-1},A_{i,j} \subseteq A_{i-1,j}$的子集选取方案数

  • 由于集合$S$的各个元素是不同的，也可以说各个元素之间是相互独立的，那么我们就可以单独对每一个元素考虑。

    • 而如果$A_{i,j}$没有当前的元素，那么以$A_{i,j}$为左上角，$A_{k,k}$为右下角的矩形所覆盖的区域都应该没有这个元素。

    • 如此一来，如果我们将有有这个元素的区域和没有这个元素的区域画上一条分界线，如图：

    

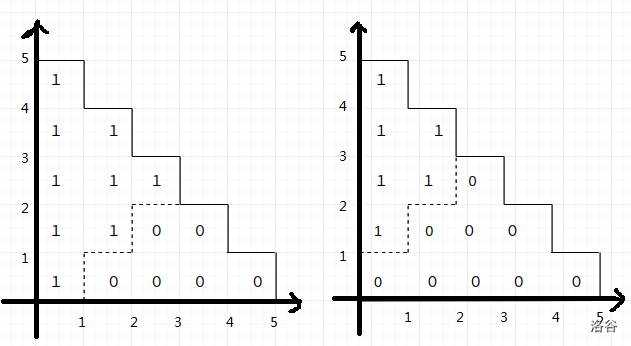
    • 如果以$A_{1,k}$左下角为原点建立坐标系，感觉这条分解线一定会经过$(0,0)$和$(i,k-i)\;\;i\in[0,k]$，并且一定是向上或向右坐标不断递增的，为什么呢？

    • 可以自己想象一下，在一个个矩形的覆盖下：一定不会向凹的情况，并且设$A_{x,y}$是$x$最小的无元素的子集，那么$A_{x,x}$一定是没有这个元素的，那么对应的分界线也就会到$A_{x,x}$的左上角，也就是$(x-1,k-x+1)$

    • 这样，问题就转化为了求从$(0,0)$走到$(i,k-i)\;\;i\in[0,k]$的方案数的问题

    • 发现，无论$i$为多少，都要走$k$步，那么就可以把问题看做是有$k$个决策，每次向上或向右，方案数自然是$2^k$。$n$个独立的元素方案数相乘，所以答案就是$2^{nk}$。

    • 同时，这也解释了$\binom{n}{0}+\binom{n}{1}+\cdots+\binom{n}{n}=\sum_{i=0}^n\binom{n}{i}=2^n$

容斥

• 容斥解决的是满足多个条件的方案数的问题，这里可以把每个条件转化为集合，例：

  • $|U|$：所有情况的方案数
  • $S_i$：满足条件$i$的方案数
  • $\begin{aligned} \left|\bigcup_{i=1}^{n}S_i\right|\end{aligned}$：满足任一一个条件的方案数
  • $\begin{aligned} \left|\bigcap_{i=1}^{n}S_{i}\right|\end{aligned}$：全部条件都满足的方案数

• 容斥的核心思想是对“至少(至多)”和“恰好（一般是）”之间的转换，重点是弄清楚哪种方案数容易求，相关的式子如下：

  • $\begin{aligned} \left|\bigcup_{i=1}^{n}S_i\right|=\sum_{m=1}^n(-1)^{m-1}\sum_{a_i<a_{i+1} }\left|\bigcap_{i=1}^mS_{a_i}\right| \end{aligned}$
  • $\begin{aligned}\left|\bigcap_{i=1}^{n}S_i\right|=|U|-\left|\bigcup_{i=1}^n\overline{S_i}\right| \end{aligned}$

• 问题一：

  $n$ 种烹饪方法，且会使用 $m$种主要食材

  使用烹饪方法 $i$ 和主要食材 $j$ 会做 $a_{i,j}$ 道不同的菜

  对于一种包含 $k(k\ge 1)$ 道菜的搭配方案而言，要求：

  • 每道菜的烹饪方法互不相同

  • 每种主要食材至多在一半的菜（即 $\lfloor \frac{k}{2} \rfloor$ 道菜）中被使用

  求搭配方案数

  • 先分析要求一，要求烹饪方法互不相同，感觉可以依次考虑对每种烹饪方法进行决策，在当前烹饪方法做不做菜？用哪种主要食材做？然后记录当前状态，以及决策对当前状态的影响，这就是一个dp了。
  • 可是发现要求二根本不好表示状态，因为对于每种食材都要满足条件，即$\begin{aligned} \left|\bigcap_{i=1}^{n}S_{i}\right|\end{aligned}$。但发现不满足条件二的方案很好求，即$\begin{aligned} \left|\bigcup_{i=1}^{n}\overline{S_i}\right|\end{aligned}$，因为只能有一种主要食材会超过一半，在dp时只需要记录一个主要食材的选用次数就可以了。
  • 于是考虑第二个式子$\begin{aligned}\left|\bigcap_{i=1}^{n}S_i\right|=|U|-\left|\bigcup_{i=1}^n\overline{S_i}\right| \end{aligned}$。通过dp计算满足要求一的所有情况数，和满足要求一而不满足要求二的方案数。
  • 注意此题dp状态需要优化，但与本次主题关联不大，故不展开分析。

• 问题二：

  一个$n\times m$的棋盘，用$c$种颜色染色，求满足条件的方案数

  • 棋盘的每一个小方格既可以染色（染成$c$种颜色中的一种），也可以不染色。
  • 棋盘的每一行至少有一个小方格被染色。
  • 棋盘的每一列至少有一个小方格被染色。
  • 每种颜色都在棋盘上出现至少一次。

  • 看上去很难，既要考虑颜色，又要考虑每一行，每一列，感觉特别不可做...
  • 我们先将颜色单独考虑。
  • 发现“出现至少一次”可以看成每种颜色都要用，即$\begin{aligned} \left|\bigcap_{i=1}^{n}S_{i}\right|\end{aligned}$，而我们发现如果有某几种颜色不用，其它颜色不考虑用不用的方法好像很好求（（其它颜色数+1）^要填的格子数），即$\begin{aligned} \left|\bigcap_{i=1}^{n}\overline{S_{i}}\right|\end{aligned}$。通过式子一和式子二共同转化，$\begin{aligned}\left|\bigcap_{i=1}^{n}S_i\right|=|U|-\left|\bigcup_{i=1}^n\overline{S_i}\right| =|U|- \sum_{m=1}^n(-1)^{m-1}\sum_{a_i<a_{i+1} }\left|\bigcap_{i=1}^mS_{a_i}\right| \end{aligned}$
    *$\begin{aligned} \sum_{a_i<a_{i+1} }\left|\bigcap_{i=1}^m\overline{S_{a_i}}\right| \end{aligned}$的意义是所有组$m$个颜色不用的方案数，组数就是$c$种颜色中选$m$种颜色，即$\binom{C}{m}$组，为了表述方便，我们设$f[i]$表示在棋盘上用最多用$i$种颜色满足要求一、二的方案数（这个待会去求），而一组的答案就为$f[c-m]$，与组数相乘即可，而全集是$f[c]$（最多用$c$种颜色就是所有情况）。所以答案为$ans=f[c]-\sum_{i=1}^{c}f[c-i]*\binom{c}{i}*(-1)^{i-1}$
  • 类似的，计算$f[i]$的时候所要考虑的要求一、二，也可以通过上面的容斥分析得到。还是通过上面的式子转化，不过此时的$\begin{aligned} \sum_{a_j<a_{j+1} }\left|\bigcap_{j=1}^k\overline{S_{a_j}}\right| \end{aligned}$就是所有组$k$列完全不涂色的方案数，一组的答案这么统计：对每一行单独考虑，答案数为$(i+1)^{m-k}$，可是一行不能全为空，就要减去一，$n$行都是独立的，相乘就是$((i+1)^{m-k}-1)^n$。这里全集就是当$k=0$时的值（0列完全不涂色就是所有的情况），所以$f[i]=((i+1)^m-1)^{n}-\sum_{k=1}^{m}*\binom{m}{k}*((i+1)^k-1)^n*(-1)^{k-1}$
  • 综合起来就可以了。