后缀排序
后缀数组
一般可用于某一个字符串的子串有关字典序的问题。
算法流程
先对该字符串的所有后缀进行排序
定义: 表示将所有后缀排序后第 小的后缀的编号。 表示后缀 的排名
采用倍增+基数排序(),(如果偷懒/怕错也可以用快排())
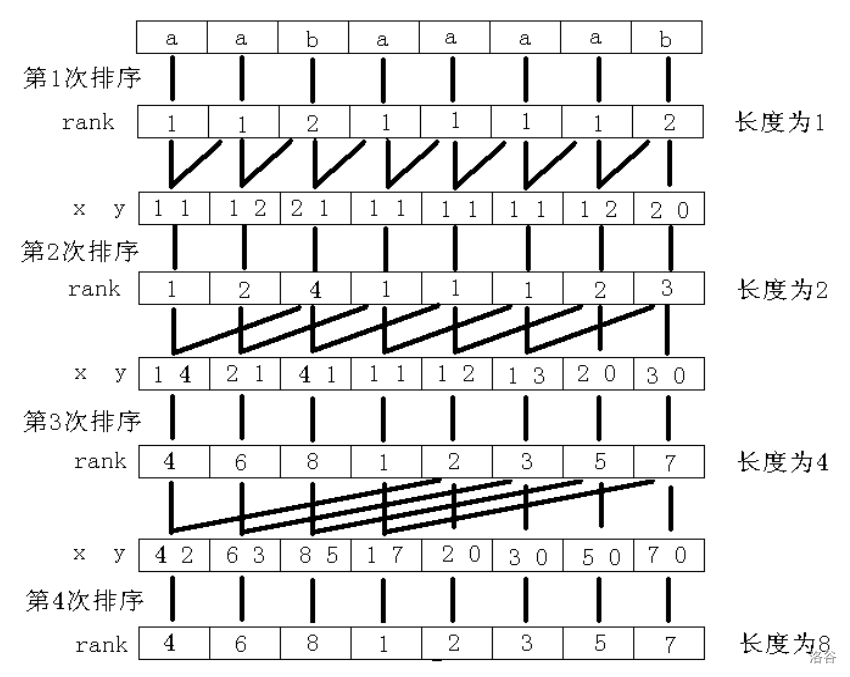
假设我们已经知道了长度为 的子串的排名 (即, 表示 在 中的排名),那么,以 为第一关键字, 为第二关键字(若 则令 为无穷小)进行排序,就可以求出 。
关于基数排序,是对每一个关键词按优先级从大到小进行一次捅排序,复杂度和值域向关,于是把一次的快排优化到了。
可以参考算法可视化进行理解
原始代码
scanf("%s", s + 1);
n = strlen(s + 1);
m = max(n, 300);
//m表示值域大小
for (i = 1; i <= n; ++i) ++cnt[rk[i] = s[i]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for (w = 1; w < n; w <<= 1) {
//按rk[i+w]第一次捅排,把排序结果存入id中
memset(cnt, 0, sizeof(cnt));
for (i = 1; i <= n; ++i) id[i] = sa[i];
for (i = 1; i <= n; ++i) ++cnt[rk[id[i] + w]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[rk[id[i] + w]]--] = id[i];
//按rk[i]第二次捅排,把排序结果存入sa中
memset(cnt, 0, sizeof(cnt));
for (i = 1; i <= n; ++i) id[i] = sa[i];
for (i = 1; i <= n; ++i) ++cnt[rk[id[i]]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[rk[id[i]]]--] = id[i];
/*
以上两次桶排也可以转化为以下简介的快排
bool paix(int x,int y){
return rk[x] == rk[y] ? rk[x + w] < rk[y + w] : rk[x] < rk[y];
}
sort(sa + 1, sa + n + 1, paix)
*/
memcpy(oldrk, rk, sizeof(rk));
//根据sa的值重新更新rk的值(因为把以前排名一致的更新)
for (p = 0, i = 1; i <= n; ++i) {
if (oldrk[sa[i]] == oldrk[sa[i - 1]] &&
oldrk[sa[i] + w] == oldrk[sa[i - 1] + w]) {
rk[sa[i]] = p;
} else {
rk[sa[i]] = ++p;
}
}
}
优化:
不需要对排序,因为你已经知道了,只需要对大于的处理成无限小,剩下的第名就是。
值域范围可以更新,我们在最后一段其实求出了当前的值域范围,用它更新。
如果值域已经是了,即已经互不相同,就可以结束
还有一些奇奇怪怪的卡常技巧(好像是连续访问一段内存会快一些)
总之,最后的代码如下
int i, m = 300, p, w;
scanf("%s", s + 1);
n = strlen(s + 1);
for (i = 1; i <= n; ++i) ++cnt[rk[i] = s[i]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for (w = 1;; w <<= 1, m = p) { // 优化二
//优化一
for (p = 0, i = n; i > n - w; --i) id[++p] = i;
for (i = 1; i <= n; ++i)
if (sa[i] > w) id[++p] = sa[i] - w;
memset(cnt, 0, sizeof(cnt));
//优化四
for (i = 1; i <= n; ++i) ++cnt[px[i] = rk[id[i]]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
memcpy(oldrk, rk, sizeof(rk));
for (p = 0, i = 1; i <= n; ++i)
//优化四
rk[sa[i]] = cmp(sa[i], sa[i - 1], w) ? p : ++p;
//优化三
if (p == n) {
for (int i = 1; i <= n; ++i) sa[rk[i]] = i;
break;
}
}
运用
算法讲解到这,好像发现了一个问题:后缀数组的用途是不是有点少啊...好像只能处理个后缀的字典序,除此之外就没得用了...
其实,后缀数组真正有用的一个重要数组才刚刚上场
数组
定义:,即第名的后缀与它前一名的后缀的最长公共前缀。
想一想,这种定义有什么好处,或者说,这种定义能做到什么
我们之前费尽周折,好不容易才把所有的后缀拍了个序,见下图
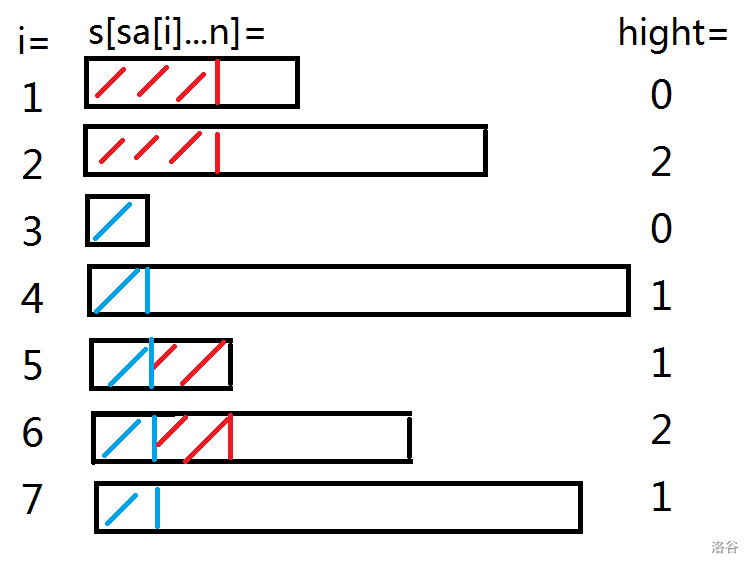
我们以排名为6的这个后缀为例(假如我们已经求出了所有)我们想知道这个后缀与所有其它后缀的前缀有多少是相同的,怎么办呢?
首先它与排名为5的后缀有个部分是相同的,与排名为4的后缀有1个部分是相同的,排名为4的有1个,排名为3的有0个,排名为2的也只有0个,发现,排名为的前缀与的前缀的公共部分就有(当也类似),为什么呢?
可以想一想字典序的相关定义,与的字典序小,说明与是相同,而与不同,那么如果 一直大于某个数,前这么多位就一直没变过。如果小于了某个数,那之后的就不可能会再一次与他重合了。
我们再想一想这个后缀还有什么性质
在求出每个之后,我们其实是对个后缀的相等信息进行了压缩,而个后缀的每一个前缀,又能完整的表示所有子串,这对我们处理子串的相等问题也大有帮助!
这就是数组在后缀数组种的运用实质,下面我们考虑怎么求出数组(终于开始将求法了...)
假设现在我们想得到(表示的是),其实可以利用,这里给出一个引理。
是不是看不懂,没关系,我们不用拘泥与这个式子,参考图想象一下。(下图中蓝色的一条和红色的一条表示后缀和后缀相等的部分)

可以发现,其实已经有了一个“保底”,即黑色下划线和绿色下划线的部分一定是相等的,但你无法保证就是啊
其实没有关系,我们可以结合字典序考虑,如果现在有字符串和(),而且已经有与前个字符是相等的,那么一定不存在一个使且与相等的前缀长度小于。
所以说,在你求的时候,已经有了的“保底”,后缀与后缀的前缀相同长度可以更长,但一定不会小于保底长度。
求的代码,就接在求出之后。
for (i = 1, k = 0; i <= n; ++i) {
if (k) --k;
while (s[i + k] == s[sa[rk[i] - 1] + k]) ++k;
ht[rk[i]] = k; // height太长了缩写为ht
}
这就是后缀数组的基本流程(还是比较好理解的吧...)
下面上一些经典的题目
咕咕咕。。。。。。。
本文作者:qwq_123
本文链接:https://www.cnblogs.com/qwq-123/p/15904946.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步