后缀自动机

后缀自动机只能对一个字符串建立（多个字符串需要广义后缀自动机），处理关于子串、字典序、出现次数等一系列问题的自动机。

后缀自动机的本质是对具有相同信息的子串（这里我们把这些子串看作一种状态）进行压缩（注意：这里后缀自动机对所有子串都进行了维护）。并且这个自动机具有图的结构，用来支持状态之间的转移，也就是一个子串加上一个字符会到另一个子串（前提是这个子串要在这个字符串中存在），还有会根据子串在原串中出现的位置的不同而形成一种树状关系（是不是感觉很高级，看不懂，没关系，我们先了解完算法之后在去看就会）

也可以添加一些其它信息（也就是在一开始自动机里并没有这些信息），这些是对后缀自动机能力的扩展，不过一般不会有太大的扩展。

算法流程

先给出对后缀自动机最为重要的一个集合——$endpos(t)$。它表示状态$t$在原字符串中所有结束位置，例对于$abcbc$，我们有 $endpos(bc)=\{2,4\}$。

我们对具有相同信息的子串就是根据$endpos$的不同而划分的，我们把$endpos$相同的看作为一个等价类。

为什么这么划分呢，因为它有许多特殊的性质来方便我们处理字符串中的子串。

性质一：

字符串 $s$ 的两个非空子串 $u$ 和 $w$（假设 $|u|≤|w|$）的 $endpos$ 相同，当且仅当字符串 $u$ 在 $s$ 中的每次出现，都是以 $w$ 后缀的形式存在的。
性质二：

考虑两个非空子串 $u$ 和 $w$（假设 $|u|≤|w|$）。那么要么 $\operatorname{endpos}(u)\cap \operatorname{endpos}(w)=\varnothing$，要么 $\operatorname{endpos}(w)\subseteq \operatorname{endpos}(u)$，取决于 $u$ 是否为 $w$ 的一个后缀。
性质三：

考虑一个 $endpos$ 等价类，将类中的所有子串按长度非递增的顺序排序。每个子串都不会比它前一个子串长，与此同时每个子串也是它前一个子串的后缀。换句话说，对于同一等价类的任一两子串，较短者为较长者的后缀，且该等价类中的子串长度恰好覆盖整个区间$ [x,y]$。

现在这三个性质还只是停留在理论上，我们还不能直接体现在算法（因为如果你对每一个维护$endpos$的话，空间...）上。所以，一个重要的来辅助表达出$endpos$的数组——$link$链接来了。

它是干什么的呢？

通过上面的性质，我们已经知道，状态 $v$ 对应于具有相同 $endpos $的等价类。我们如果定义 $w$ 为这些字符串中最长的一个，则所有其它的字符串都是 $w$ 的后缀。

我们还知道字符串 $w$ 的前几个后缀（按长度降序考虑）全部包含于这个等价类，且所有其它后缀（至少有一个——空后缀）在其它的等价类中。我们记 $t$ 为最长的这样的后缀，然后将 $v$ 的后缀链接连到 $t$ 上。

这个$link$也拥有一些优秀的性质：

性质四：

所有后缀链接构成一棵根节点为 $t_0$(开始节点) 的树。

后缀链接 $link(v)$ 连接到的状态对应于严格更短的字符串（后缀链接的定义）。因此，沿后缀链接移动，我们总是能到达对应空串的初始状态 $t_0$。
性质五：

该树的每个父节点的 $endpos $ 都包含在子节点的 $endpos $ ，即$\operatorname{endpos}(v)\subsetneq \operatorname{endpos}(\operatorname{link}(v)),$

由性质 2，任意一个 SAM 的两个要么完全没有交集，要么其中一个是另一个的子集。
性质六：

该树的每个父节点的表示的子串都是子节点的子串的后缀

到这里，我们发现$link$链接的存在，把维护了整个自动机的一个树的形态，而结合性质三我们知道每个状态都可以用一个长度区间$[x,y]$表示一个$endpos$等价类(设状态$v$最长的子串为$S(|S|=y)$)，表示的是$S[1\sim x],S[1\sim x+1],S[1\sim x+2]...S[1\sim y-1],S$这些子串，并且$link[v]$对应的区间的右端点一定是$x-1$，所以我们可以就用以下两个变量大概表示$endpos$：

$len[x]$：表示状态$x$中长度最长的子串的长度
$link[x]$：与状态$x$不是同一个$endpos$等价类，但为状态最长后缀所对应的状态

这样通过$link$和$len$，我们能够表达出该$endpos$对应的长度区间$[len[link[v]]+1,len[v]]$。

这也是后缀自动机对子串压缩的奥秘，现用endpos表示所有的子串，然后通过$endpos$的性质，转化为一段长度区间，最后通过$link$和$len$表达出来（所以$link$的实质就在这），所以，我们在后缀自动机里用到$link$和$len$的时候（虽然有时候$link/len$也会单独运用在题目中），要想到其背后的$endpos$。

上面是大段对endpos的解释，是为了更好理解下面对后缀自动机的构造，我们会通过$endpos$用极少的状态(最大为$2n-1$)表示所有的子串

构造

在构造中，我们要维护$link,len,next$（用来实现状态之间的转移）。

首先注意，后缀自动机是一个在线算法，每一次插入一个字符（设这个位置为$n$），然后对$S[1\sim n],S[2\sim n],S[3\sim n]...S[n\sim n]$这些子串建立状态和更新已有状态。

这$n$个子串中，一定会有子串对应状态的$endpos=\{n\}$（至少$S[1\sim n]$是），所以这里加入一个新状态，设这个新状态为$p$，所以$len[p]=n$

如果这$n$个子串都没在原串（$S[1\sim n-1]$）中出现过，对$endpos[p]$的更新就没了。

而如果有一段（$S[X\sim n]...S[n\sim n]$）已经出现过，那么我们就要得到表示$S[X\sim n]$这个字符串的状态$y$，并且用这个$y$更新$link[p]$。

为啥不能直接更新呢？

那么我们怎么得到这个$y$呢？

考虑$S[X\sim n]$可以拆解为$S[X\sim n-1]+S[n]$，而$S[X\sim n-1]$正是$S[1\sim n-1]$的后缀，那么根据性质六，我们就可以在$S[1\sim n-1]$对应的状态（设为$last$）向祖先跳，如果存在$x\in last$的父亲，且$next[x][S[n]]!=0$。那么$x$最长的子串就表示$S[X\sim n-1]$，$y$就是$next[x][S[n]]$。否则$link[x]=$初始状态。

如果要复制$y$之后为啥要更新$S[X\sim n-1]$对应状态及其祖先的转移呢?

因为$endpos[clone]$已经更新了（多了$\{n\}$），与$endpos[y]$不同了，那么所有本应该转移到$y$，且满足长度小于$len[clone]-1$的子串都应该更新为$clone$，而我们发现这些子串都是在$x$或$x$的祖先中（就是$S[X\sim n-1]$对应状态及其祖先），更新它们即可。

现在我们讲新子串带来的转移的更新。

首先，对于$S[1\sim n],S[2\sim n],S[3\sim n]...S[n\sim n]$这些子串，可以拆成$S[1\sim n-1]+S[n],S[2\sim n-1]+S[n],S[3\sim n-1]+S[n]...S[n]$，那么我们需要更新的转移，就是$S[1\sim n-1],S[2\sim n-1],S[3\sim n-1]...S[n-1]$对应的状态，那么我们在顺着$last$的祖先更新转移，把所有$x\in last$的父亲，且$next[x][s[n]]=0$的更新。如果是上文提到的已经出现过的一段子串（$next[x][s[n]]!=0$），那么它们的状态是已经存在的了，那么就不需它要转移，结束。

我们可以结合这几张图感受一下（黄色边表示link）：

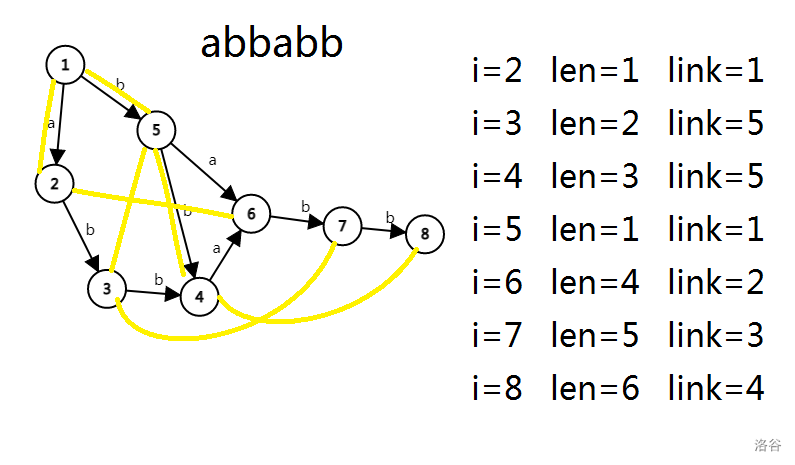
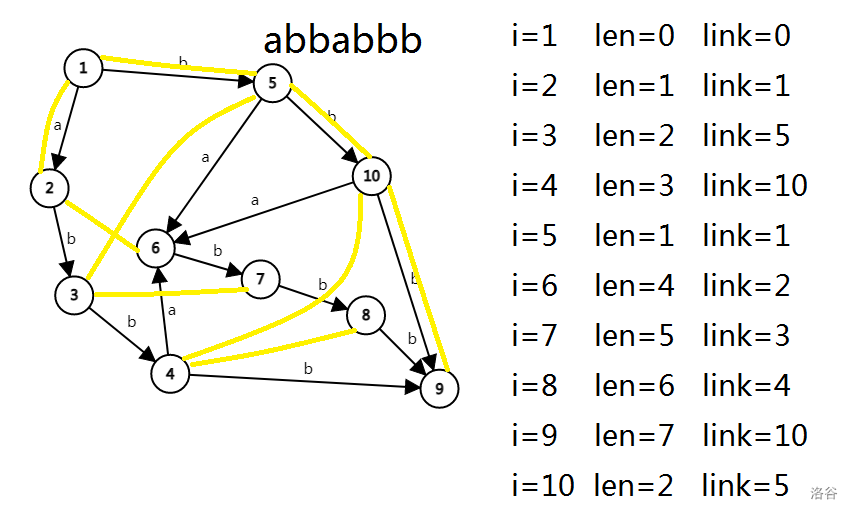
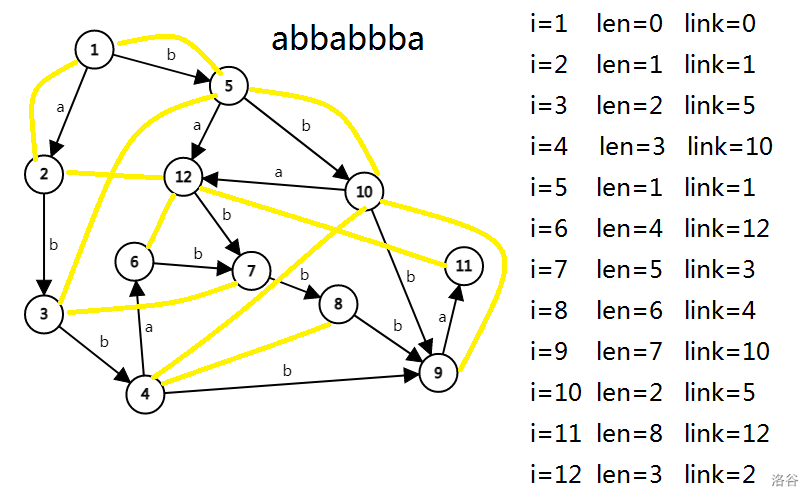
发现得到$y$的过程和更新转移的过程很像，我们可以合并一下，代码如下：

void sam(int cc){//cc=S[n]
	int p=++top;
	s[p].len=s[la].len+1;//len[p]=n,而len[la]=p-1;
	int x=la;
	while(x&&!s[x].ne[cc]){//想找一个祖先且ne[x][cc]!=0的状态x
		s[x].ne[cc]=p;//在查找的时候更新转移
		x=s[x].li;
	}
	if(!x)s[p].li=1;//状态赋值为初始状态
	else{
		int y=s[x].ne[cc];
		if(s[x].len+1==s[y].len)s[p].li=y;//如果len[y]就是|S[X~n]|
		else{
			int st=++top;	//复制y状态
			s[st]=s[y];
			s[st].len=s[x].len+1;	//更新新状态的endpos的右端点
			while(x&&s[x].ne[cc]==y){
				s[x].ne[cc]=st;
				x=s[x].li;
			}
			s[y].li=s[p].li=st;
		}
	}
	la=p;
}

后缀自动机有什么用呢?

主要体现在根据$endpos$性质，运用$link/len$来做事

$link$树
$len$
扩展

posted @ 2022-02-17 15:42 qwq_123 阅读(75) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

qwq123

后缀自动机

后缀自动机

算法流程

构造

公告