cart中回归树的原理和实现

前面说了那么多，一直围绕着分类问题讨论，下面我们开始学习回归树吧，

cart生成有两个关键点

• 如何评价最优二分结果
• 什么时候停止和如何确定叶子节点的值

 cart分类树采用gini系数来对二分结果进行评价，叶子节点的值使用多数表决，那么回归树呢？我们直接看之前的一个数据集（天气与是否出去玩，是否出去玩改成出去玩的时间）

sunny    hot    high    FALSE    25
sunny    hot    high    TRUE    30
overcast    hot    high    FALSE    46
rainy    mild    high    FALSE    45
rainy    cool    normal    FALSE    52
rainy    cool    normal    TRUE    23
overcast    cool    normal    TRUE    43
sunny    mild    high    FALSE    35
sunny    cool    normal    FALSE    38
rainy    mild    normal    FALSE    46
sunny    mild    normal    TRUE    48
overcast    mild    high    TRUE    52
overcast    hot    normal    FALSE    44
rainy    mild    high    TRUE    30

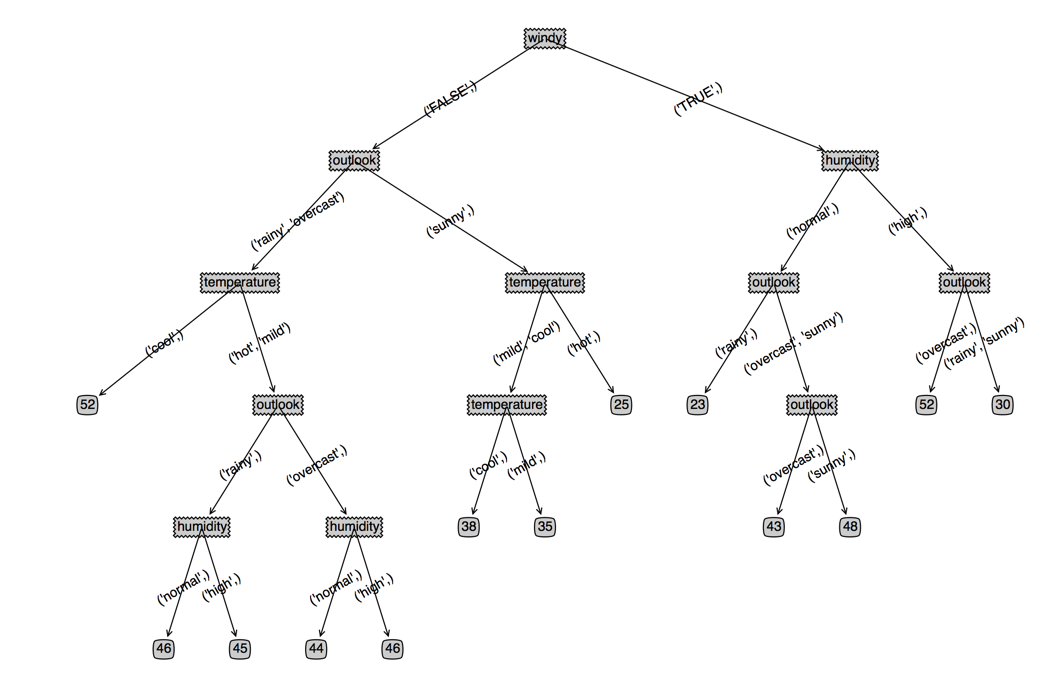
如果用分类树来做，结果就是这样的，一个结果值一个节点

回归树切分数据集和分类树是一样的，那么我们如何评价一个数据集划分的好坏呢？分类树是用gini系数衡量数据集的类别的混乱程度，同样，我们也可以衡量数据集的回归值的混乱程度，比较经典的是方差和标准差，由于我们需要得到和回归值接近的值作为叶子节点的值，我们这里使用标准差吧

n是回归值的个数，u是平均值，x是每个回归值，S是标准差（standard deviation）

第二个问题：什么时候停止和如何确定叶子节点的值？

分类树是特征用完或者类别都一样；对于回归问题回归值都一样的概率比较小，由于我们过程中不减少特征，所以最后肯定是一个样本一个分支。

有人说当分支的S小于总体的5%，分支就可以结束，然后节点的值取平均值

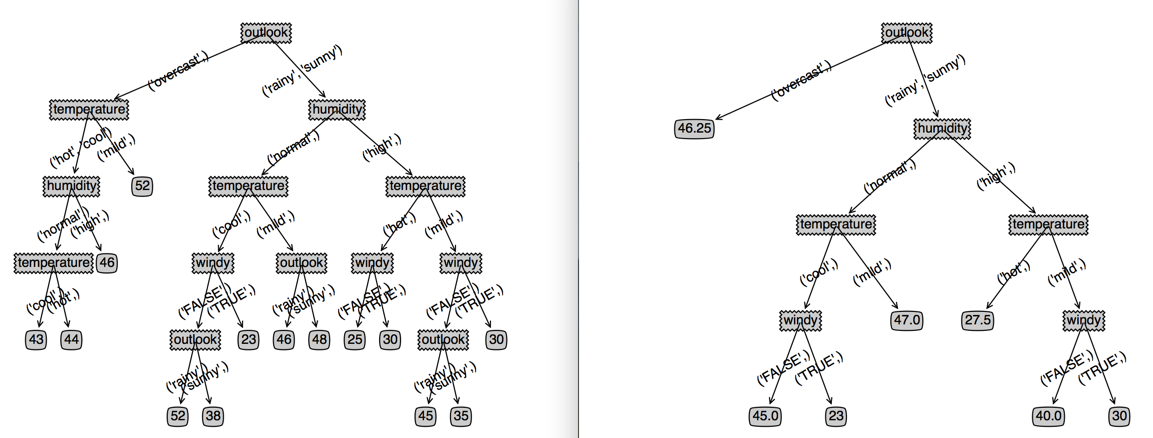
我们看下这样有效果不？左边是没有停止原始的回归树，右边是加上结束条件的回归树，感觉效果还可以，这样回归树就完成了

对比回归树和分类树的实现，发现基本是就仅仅是一个函数的区别，到这里明白为什么叫分类回归树了吗？

就是同样的代码，只需要改变一个函数，就可以实现分类或者回归的功能的了。

下面附上回归树的完整代码

# regression_tree.py
# coding:utf8
from itertools import *
from numpy import *
import operator,math
def calStDev(dataSet):
    classList = [float(example[-1]) for example in dataSet]
    n=len(classList)
    u=sum(classList)/n
    total=0
    for x in classList:
        total+=(x-u)*(x-u)
    S = math.sqrt(total)
    return S,u

def splitDataSet(dataSet, axis, values):
    retDataSet = []
    if len(values) < 2:
        for featVec in dataSet:
            if featVec[axis] == values[0]:#如果特征值只有一个，不抽取当选特征
                reducedFeatVec = featVec[:axis]     
                reducedFeatVec.extend(featVec[axis+1:])
                retDataSet.append(reducedFeatVec)
    else:
        for featVec in dataSet:
            for value in values:
                if featVec[axis] == value:#如果特征值多于一个，选取当前特征
                    retDataSet.append(featVec)

    return retDataSet    
# 传入的是一个特征值的列表，返回特征值二分的结果
def featuresplit(features):
    count = len(features)#特征值的个数
    if count < 2:
        # print features
        # print "please check sample's features,only one feature value"
        return ((features[0],),)
    # 由于需要返回二分结果，所以每个分支至少需要一个特征值，所以要从所有的特征组合中选取1个以上的组合
    # itertools的combinations 函数可以返回一个列表选多少个元素的组合结果，例如combinations(list,2)返回的列表元素选2个的组合
    # 我们需要选择1-（count-1）的组合
    featureIndex = range(count)
    featureIndex.pop(0) 
    combinationsList = []    
    resList=[]
    # 遍历所有的组合
    for i in featureIndex:
        temp_combination = list(combinations(features, len(features[0:i])))
        combinationsList.extend(temp_combination)
        combiLen = len(combinationsList)
    # 每次组合的顺序都是一致的，并且也是对称的，所以我们取首尾组合集合
    # zip函数提供了两个列表对应位置组合的功能
    resList = zip(combinationsList[0:combiLen/2], combinationsList[combiLen-1:combiLen/2-1:-1])
    return resList
# 返回最好的特征以及二分特征值
def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1      #
    bestStDev = inf; bestFeature = -1;bestBinarySplit=()
    for i in range(numFeatures):        #遍历特征
        featList = [example[i] for example in dataSet]#得到特征列
        uniqueVals = list(set(featList))       #从特征列获取该特征的特征值的set集合
        # 三个特征值的二分结果：
        # [(('young',), ('old', 'middle')), (('old',), ('young', 'middle')), (('middle',), ('young', 'old'))]
        for split in featuresplit(uniqueVals):
            StDev = 0.0
            if len(split)==1:
                continue
            (left,right)=split
            # print split,
            # 对于每一个可能的二分结果计算gini增益
            # 左增益
            left_subDataSet = splitDataSet(dataSet, i, left)
            left_prob = len(left_subDataSet)/float(len(dataSet))
            S,u = calStDev(left_subDataSet)
            StDev += left_prob * S
            # 右增益
            right_subDataSet = splitDataSet(dataSet, i, right)
            right_prob = len(right_subDataSet)/float(len(dataSet))
            S,u = calStDev(right_subDataSet)
            StDev += right_prob * S
            # print StDev
            if (StDev < bestStDev):       #比较是否是最好的结果
                bestStDev = StDev         #记录最好的结果和最好的特征
                bestFeature = i
                bestBinarySplit=(left,right)
    return bestFeature,bestBinarySplit,bestStDev                  

def majorityCnt(classList):
    classCount={}
    for vote in classList:
        if vote not in classCount.keys(): classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

def createTree(dataSet,labels,originalS):
    classList = [example[-1] for example in dataSet]
    # print dataSet
    if classList.count(classList[0]) == len(classList): 
        return classList[0]#所有的类别都一样，就不用再划分了
    if len(dataSet) == 1: #如果没有继续可以划分的特征，就多数表决决定分支的类别
        return majorityCnt(classList)
    bestFeat,bestBinarySplit,bestStDev = chooseBestFeatureToSplit(dataSet)
    if bestStDev < 0.05*originalS:
        return 1.0*sum(classList)/len(classList)
    # print bestFeat,bestBinarySplit,labels
    bestFeatLabel = labels[bestFeat]
    if bestFeat==-1:
        return majorityCnt(classList)
    myTree = {bestFeatLabel:{}}
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = list(set(featValues))
    for value in bestBinarySplit:
        subLabels = labels[:]       # #拷贝防止其他地方修改
        if len(value)<2:
            del(subLabels[bestFeat])
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels,originalS)
    return myTree  

filename="regression_sample"
dataSet=[];labels=[];
with open(filename) as f:
    for line in f:
        fields=line.strip("\n").split("\t")
        t=fields[0:-1]
        t.append(int(fields[-1]))
        dataSet.append(t)
labels=["outlook","temperature","humidity","windy"]
# print dataSet
originalS,u=calStDev(dataSet)
# print originalS,u
tree= createTree(dataSet,labels,originalS)
print tree