推荐系统实践--基于用户的协同过滤算法

基于邻域的算法是推荐系统中最基本的算法，该算法不仅在学术界得到了深入研究，而且在业界得到了广泛应用。基于邻域的算法分为两大类，一类是基于用户的协同过滤算法，另一类是基于物品的协同过滤算法。

我们先来看看基于用户的协同过滤算法，基于物品的协同过滤算法大体思路和基于用户的差不多，可以自己参考对比学习。

基于用户的协同过滤算法

每年新学期开始，刚进实验室的师弟总会问师兄相似的问题，比如“我应该买什么专业书啊”、“我应该看什么论文啊”等。这个时候，师兄一般会给他们做出一些推荐。这就是现实中个性化推荐的一种例子。在这个例子中，师弟可能会请教很多师兄，然后做出最终的判断。师弟之所以请教师兄，一方面是因为他们有社会关系，互相认识且信任对方，但更主要的原因是师兄和师弟有共同的研究领域和兴趣。那么，在一个在线个性化推荐系统中，当一个用户A需要个性化推荐时，可以先找到和他有相似兴趣的其他用户，然后把那些用户喜欢的、而用户A没有听说过的物品推荐给A。这种方法称为基于用户的协同过滤算法。

基于用户的协同过滤算法主要包括两个步骤。

(1) 找到和目标用户兴趣相似的用户集合。

(2) 找到这个集合中的用户喜欢的，且目标用户没有听说过的物品推荐给目标用户。

步骤(1)的关键就是计算两个用户的兴趣相似度。这里，协同过滤算法主要利用行为的相似度计算兴趣的相似度。给定用户u和用户v，令N(u)表示用户u曾经有过正反馈的物品集合，令N(v)为用户v曾经有过正反馈的物品集合。那么，我们可以通过如下的Jaccard公式简单地计算u和v的兴趣相似度或者通过余弦公式：

      jaccard                                                                             余项公式：

：                         

 

 

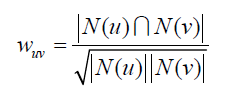
这个一个行为记录                                             我们可以根据余弦公式计算如下

                             

以余弦相似度为例，实现该相似度可以利用下面的伪代码：

def UserSimilarity(train):
    W = dict()
    for u in train.keys():
        for v in train.keys():
            if u == v:
                continue
            W[u][v] = len(train[u] & train[v])
            W[u][v] = /= math.sqrt(len(train[u]) * len(train[v]) * 1.0)
    return W

这种方法的时间复杂度是O(|U|*|U|)，这在用户数很大时非常耗时。事实上，很多用户相互之间并没有对同样的物品产生过行为，即很多时候N(u)^ N(v) = 0。上面的算法将很多时间浪费在了计算这种用户之间的相似度上。如果换一个思路，我们可以首先计算出N(u)^ N(v) != 0 的用户对(u,v)，然后再对这种情况除以分母sqrt(N(u)*N(v)) 。

为此，可以首先建立物品到用户的倒排表，对于每个物品都保存对该物品产生过行为的用户列表。令稀疏矩阵C[u][v]= N(u)^ N(v) 。那么，假设用户u和用户v同时属于倒排表中K个物品对应的用户列表，就有C[u][v]=K。从而，可以扫描倒排表中每个物品对应的用户列表，将用户列表中的两两用户对应的C[u][v]加1，最终就可以得到所有用户之间不为0的C[u][v]

def UserSimilarity(train):
    # build inverse table for item_users
    item_users = dict()
    for u, items in train.items():
        for i in items.keys():
            if i not in item_users:
                item_users[i] = set()
            item_users[i].add(u)
    #calculate co-rated items between users
    C = dict()
    N = dict()
    for i, users in item_users.items():
        for u in users:
            N[u] += 1
            for v in users:
                if u == v:
                    continue
                C[u][v] += 1
    #calculate finial similarity matrix W
    W = dict()
    for u, related_users in C.items():
        for v, cuv in related_users.items():
            W[u][v] = cuv / math.sqrt(N[u] * N[v])
    return W

 

下面是按照想法建立的稀疏矩阵，对于物品a，将W[A][B]和W[B][A]加1，对于物品b，将W[A][C]和W[C][A]加1，以此类推，扫描完所有物品后，我们可以得到最终的W矩阵，这里的W是余弦相似度中的分子部分，然后将W除以分母可以得到最终的用户兴趣相似度

得到用户之间的兴趣相似度后，UserCF算法会给用户推荐和他兴趣最相似的K个用户喜欢的物品。上面右边公式度量了UserCF算法中用户u对物品i的感兴趣程度：其中，S(u, K)包含和用户u兴趣最接近的K个用户，N(i)是对物品i有过行为的用户集合，Wuv是用户u和用户v的兴趣相似度，Rvi代表用户v对物品i的兴趣，因为使用的是单一行为的隐反馈数据，所以所有的Rvi=1。

如下代码实现了上面的UserCF推荐算法：

def Recommend(user, train, W):
    rank = dict()
    interacted_items = train[user]
    for v, wuv in sorted(W[u].items, key=itemgetter(1), reverse=True)[0:K]:
        for i, rvi in train[v].items:
        if i in interacted_items:
            #we should filter items user interacted before
            continue
        rank[i] += wuv * rvi
    return rank

选取K=3，用户A对物品c、e没有过行为，因此可以把这两个物品推荐给用户A。根据UserCF算法，用户A对物品c、e的兴趣是：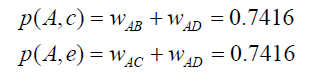

用户相似度计算的改进

如果两个用户都曾经买过《新华字典》，这丝毫不能说明他们兴趣相似，因为绝大多数中国人小时候都买过《新华字典》。但如果两个用户都买过《数据挖掘导论》，那可以认为他们的兴趣比较相似，因为只有研究数据挖掘的人才会买这本书。换句话说，两个用户对冷门物品采取过同样的行为更能说明他们兴趣的相似度。因此，John S. Breese在论文①中提出了如下公式，根据用户行为计算用户的兴趣相似度：

分子中的倒数惩罚了用户u和用户v共同兴趣列表中热门物品对他们相似度的影响。N(i)是对物品i有过行为的用户集合，越热门，N(i)越大

def UserSimilarity(train):
    # build inverse table for item_users
    item_users = dict()
    for u, items in train.items():
        for i in items.keys():
            if i not in item_users:
                item_users[i] = set()
            item_users[i].add(u)
    #calculate co-rated items between users
    C = dict()
    N = dict()
    for i, users in item_users.items():
        for u in users:
            N[u] += 1
            for v in users:
                if u == v:
                    continue
            C[u][v] += 1 / math.log(1 + len(users))
    #calculate finial similarity matrix W
    W = dict()
    for u, related_users in C.items():
        for v, cuv in related_users.items():
            W[u][v] = cuv / math.sqrt(N[u] * N[v])
    return W