观看视频时的拖动行为研究&对数正态分布拟合实践

在移动端观看视频的时候，大家一般会有一些拖动，那么拖动的时间间隔的分布是否有规律呢？

首先定义用户拖动的间隔和前后拖动（例如从第10秒拖动到23秒，间隔是+23（前拖）；从第100秒拖动到91秒，间隔是-9（后拖））

我们以10秒为一个级别，统计用户拖动分布的频率分布图如下，显然，前拖和后拖应该不是同一个分布

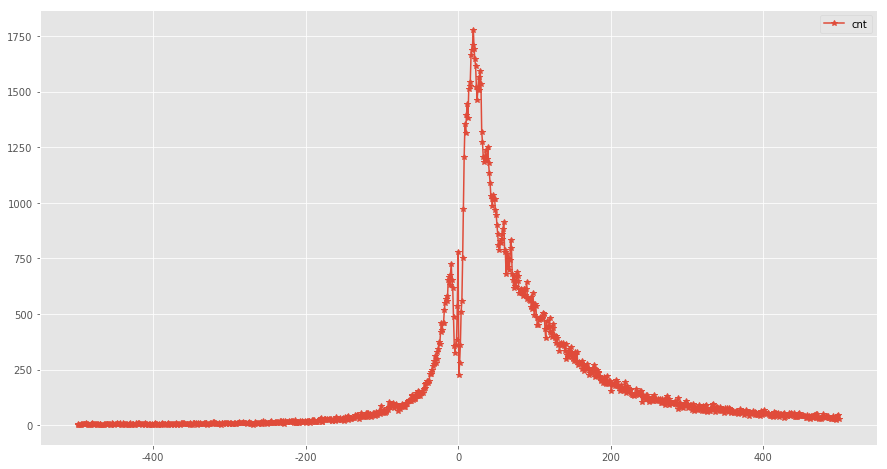
我们详细看下前拖，这看起来很像是对数正态分布的分布图

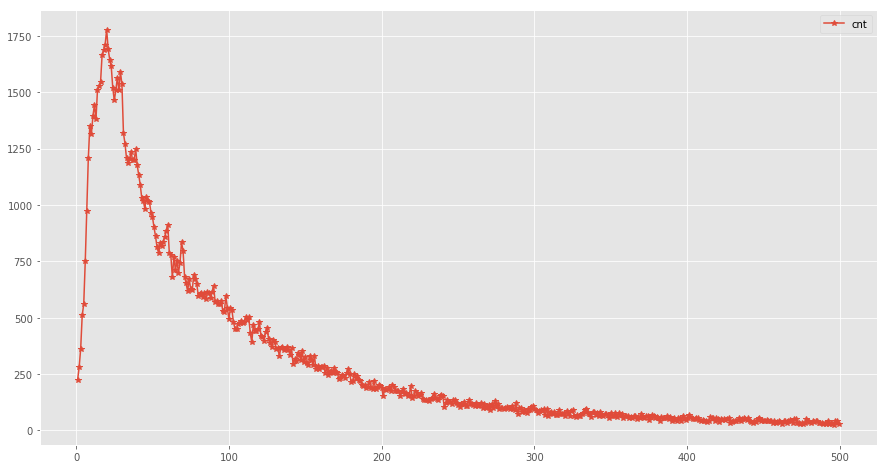
对拖动间隔对数化，看起来有点像正态分布的样子，下面我们尝试拟合一下

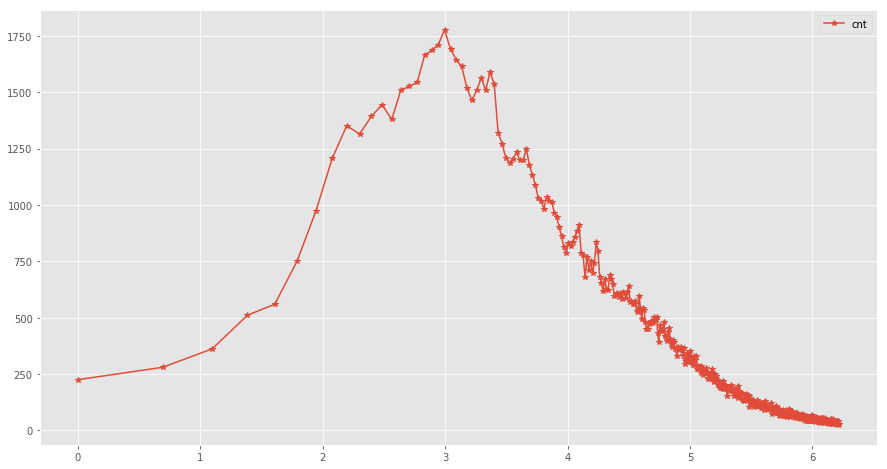
我们来看下对数正态分布的定义和相关公式

对于 $x>0$

下面我们求解原始分布的平均值（期望值）和方差，然后求解 $\mu$

可以看到，收集20w次的拖动数据模拟的效果，基本是很接近了

最后说下一开始的错误的想法，可能也是一些小伙伴在一开始碰到对数正态分布的“顺其自然”的想法

# 求解流程
# 1.拖动数据取出前拖数据
# 2.对前拖数据对数化
# 3.*对对数化数据求解正态分布参数*
# 3.1找到峰值点对应的采样值（mul）
# 3.2对峰值点采样点较多的一侧计算标准差（sig）
# 4.生成正态分布X~(mul, sig) temp
# 5.对比temp的log分布和原分布的重合性

其实这个想法理论上也没有问题，因为如果 $Y$

问题在于原始的对数正态分布的数据，对数化为的分布虽然符合正态分布，但是采样却是失真了，我们可以看到正态分布左侧的样本点明显稀疏很多，顶部的样本点分布也不合理

这就会导致3.2计算标准差面临挑战，所以这样的求解思路虽然可能正确，但面临着数据失真的问题

下面附上原始代码

# coding: utf-8
# In[1]:
import warnings
import math
warnings.filterwarnings('ignore')
# 导入pandas模块并取别名pd
import pandas as pd
# 指定查看pandas数据时展示最大的行数和列数
pd.options.display.max_rows = 100
pd.options.display.max_columns = 100
# 导入matplotlib模块用于绘图
import matplotlib
# 作用就是在你调用plot()进行画图或者直接输入Figure的实例对象的时候，会自动的显示并把figure嵌入到console中
get_ipython().magic(u'matplotlib inline')
# 使用自带的样式进行美化
matplotlib.style.use('ggplot')
# 从matplotlib中导入pyplot并取别名为plt
from matplotlib import pyplot as plt
# 一些图中想正常显示中文的基本配置
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
myfont = matplotlib.font_manager.FontProperties(fname=u"simsun.ttc", size=14)
# 其他的一些库
import math

import numpy as np
pd.set_option('max_colwidth', 500)

# In[2]:
original = pd.read_csv("./seek_original.csv")
original.shape

# In[3]:
show = original[(original['seekgap'] > -500) & (original['seekgap'] < 500)]
show.shape

# In[4]:
plt.figure(figsize=(15, 8))
plt.hist(show.seekgap, bins=1000)
plt.legend()

# In[5]:
show_cnt = show.groupby(['seekgap'], as_index=False)[
    'seekgap'].agg({'cnt': 'count'})
show_cnt.head(2)

# In[6]:
plt.figure(figsize=(15, 8))
plt.plot(show_cnt.seekgap, show_cnt.cnt, marker="*")
plt.legend()

# In[7]:
plt.figure(figsize=(15, 8))
plt.plot(show_cnt[show_cnt['seekgap'] > 0].seekgap,
         show_cnt[show_cnt['seekgap'] > 0].cnt, marker="*")
plt.legend()

# In[8]:
plt.figure(figsize=(15, 8))
plt.plot(np.log2(show_cnt[show_cnt['seekgap'] > 0].seekgap),
         show_cnt[show_cnt['seekgap'] > 0].cnt, marker="*")
plt.legend()

# In[9]:
forward_seek = original[original.seekgap > 0]
forward_seek.shape

# In[10]:
expect = np.mean(forward_seek.seekgap)
std = np.std(forward_seek.seekgap)
expect, std

# In[11]:
mul = np.round(np.log(expect) - 0.5 * np.log(1 + (std**2) / (expect**2)), 5)
sig = np.round(np.log(1 + (std**2) / (expect**2)), 5)
mul, sig

# In[12]:
log_sample = pd.DataFrame(np.random.lognormal(mul, sig, 220000), columns=['x'])
log_sample.shape

# In[13]:
mock_show = log_sample[(log_sample['x'] > -500) & (log_sample['x'] < 500)]
mock_show.shape

# In[14]:
mock_show['x'] = np.round(mock_show.x)
mock_show.head(2)

# In[15]:
mock_cnt = mock_show.groupby(['x'], as_index=False)['x'].agg({'cnt': 'count'})
mock_cnt.shape

# In[16]:
plt.figure(figsize=(15, 8))
plt.plot(show_cnt[show_cnt['seekgap'] > 0].seekgap,
         show_cnt[show_cnt['seekgap'] > 0].cnt, marker="*", label='original')
plt.plot(mock_cnt[mock_cnt['x'] > 0].x, mock_cnt[mock_cnt['x']
                                                 > 0].cnt, marker=".", color='b', label='mock')
plt.legend()

# In[17]:
show_cnt.cnt.sum(), mock_cnt.cnt.sum()

# In[18]:
# 下面是正确缺面临数据求解问题的思路

# In[19]:
# 求解流程
# 1.拖动数据取出前拖数据
# 2.对前拖数据对数化
# 3.*对对数化数据求解正态分布参数*
# 3.1找到峰值点对应的采样值（mul）
# 3.2对峰值点采样点较多的一侧计算标准差（sig）
# 4.生成正态分布X~(mul, sig) temp
# 5.对比temp的log分布和原分布的重合性

View Code

posted @ 2020-01-15 15:38 2BiTT 阅读(589) 评论(0) 编辑收藏举报

刷新页面返回顶部

2BiTT

观看视频时的拖动行为研究&对数正态分布拟合实践

公告