丢弃奇数位置上的元素

丢弃奇数位置上的元素

题目描述

给定 [1, n] 上的连续数字，每次去掉奇数位置上的数，当最后只剩一个数字时，这个数字是多少。

题解

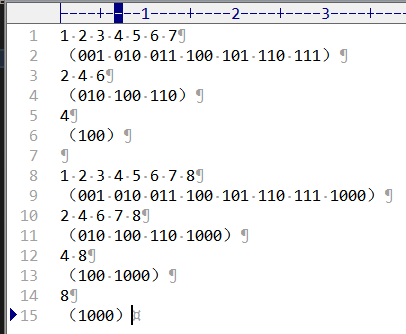
如图所示：

将每个数字转换成二进制表示，可以发现，在第 i 轮删掉的数字，都是在二进制表示中从右->左，第 i 个位置为 1 的数字。因此，留下来的数字，肯定是从左到右，10000... 这样的 二进制数，因为如果低位有 1 的话，在第 i 轮之后就会被删除。
对于 [1, n] 这些数，满足这样的数字为 2^k <= n 中的 k 取最大值时，能得到的数字 2^max_k。

例如当 n = 7 时， max_k = 2;
例如当 n = 8 时， max_k = 3;

max_k = log2(n)