Nowcoder Sum of Maximum ( 容斥原理 && 拉格朗日插值法 )

题目链接

题意 :

 

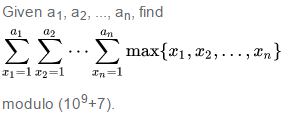
分析 :

分析就直接参考这个链接吧 ==> Click here

大体的思路就是

求和顺序不影响结果、故转化一下思路枚举每个最大值对答案的贡献最后累加就是结果

期间计数的过程要用到容斥和多项式求和 ( 利用拉格朗日求即可 ) 具体参考给出的链接

 

#include<bits/stdc++.h>
#define LL long long
#define ULL unsigned long long

#define scl(i) scanf("%lld", &i)
#define scll(i, j) scanf("%lld %lld", &i, &j)
#define sclll(i, j, k) scanf("%lld %lld %lld", &i, &j, &k)
#define scllll(i, j, k, l) scanf("%lld %lld %lld %lld", &i, &j, &k, &l)

#define scs(i) scanf("%s", i)
#define sci(i) scanf("%d", &i)
#define scd(i) scanf("%lf", &i)
#define scIl(i) scanf("%I64d", &i)
#define scii(i, j) scanf("%d %d", &i, &j)
#define scdd(i, j) scanf("%lf %lf", &i, &j)
#define scIll(i, j) scanf("%I64d %I64d", &i, &j)
#define sciii(i, j, k) scanf("%d %d %d", &i, &j, &k)
#define scddd(i, j, k) scanf("%lf %lf %lf", &i, &j, &k)
#define scIlll(i, j, k) scanf("%I64d %I64d %I64d", &i, &j, &k)
#define sciiii(i, j, k, l) scanf("%d %d %d %d", &i, &j, &k, &l)
#define scdddd(i, j, k, l) scanf("%lf %lf %lf %lf", &i, &j, &k, &l)
#define scIllll(i, j, k, l) scanf("%I64d %I64d %I64d %I64d", &i, &j, &k, &l)

#define lson l, m, rt<<1
#define rson m+1, r, rt<<1|1
#define lowbit(i) (i & (-i))
#define mem(i, j) memset(i, j, sizeof(i))

#define fir first
#define sec second
#define VI vector<int>
#define ins(i) insert(i)
#define pb(i) push_back(i)
#define pii pair<int, int>
#define VL vector<long long>
#define mk(i, j) make_pair(i, j)
#define all(i) i.begin(), i.end()
#define pll pair<long long, long long>

#define _TIME 0
#define _INPUT 0
#define _OUTPUT 0
clock_t START, END;
void __stTIME();
void __enTIME();
void __IOPUT();
using namespace std;
const int maxn = 1e3 + 10;
const LL mod = 1e9 + 7;

LL pow_mod(LL a, LL b)
{
    a %= mod;
    LL ret = 1;
    while(b){
        if(b & 1) ret = (ret * a) % mod;
        a = ( a * a ) % mod;
        b >>= 1;
    }
    return ret;
}

namespace polysum {
    #define rep(i,a,n) for (int i=a;i<n;i++)
    #define per(i,a,n) for (int i=n-1;i>=a;i--)
    const int D=2010;
    LL a[D],f[D],g[D],p[D],p1[D],p2[D],b[D],h[D][2],C[D];
    LL powmod(LL a,LL b){LL res=1;a%=mod;assert(b>=0);for(;b;b>>=1){if(b&1)res=res*a%mod;a=a*a%mod;}return res;}
    LL calcn(int d,LL *a,LL n) { // a[0].. a[d]  a[n]
        if (n<=d) return a[n];
        p1[0]=p2[0]=1;
        rep(i,0,d+1) {
            LL t=(n-i+mod)%mod;
            p1[i+1]=p1[i]*t%mod;
        }
        rep(i,0,d+1) {
            LL t=(n-d+i+mod)%mod;
            p2[i+1]=p2[i]*t%mod;
        }
        LL ans=0;
        rep(i,0,d+1) {
            LL t=g[i]*g[d-i]%mod*p1[i]%mod*p2[d-i]%mod*a[i]%mod;
            if ((d-i)&1) ans=(ans-t+mod)%mod;
            else ans=(ans+t)%mod;
        }
        return ans;
    }
    void init(int M) {
        f[0]=f[1]=g[0]=g[1]=1;
        rep(i,2,M+5) f[i]=f[i-1]*i%mod;
        g[M+4]=powmod(f[M+4],mod-2);
        per(i,1,M+4) g[i]=g[i+1]*(i+1)%mod;
    }
    LL polysum(LL m,LL *a,LL n) { // a[0].. a[m] \sum_{i=0}^{n-1} a[i]
        LL b[D];
        for(int i=0;i<=m;i++) b[i]=a[i];
        b[m+1]=calcn(m,b,m+1);
        rep(i,1,m+2) b[i]=(b[i-1]+b[i])%mod;
        return calcn(m+1,b,n-1);
    }
    LL qpolysum(LL R,LL n,LL *a,LL m) { // a[0].. a[m] \sum_{i=0}^{n-1} a[i]*R^i
        if (R==1) return polysum(n,a,m);
        a[m+1]=calcn(m,a,m+1);
        LL r=powmod(R,mod-2),p3=0,p4=0,c,ans;
        h[0][0]=0;h[0][1]=1;
        rep(i,1,m+2) {
            h[i][0]=(h[i-1][0]+a[i-1])*r%mod;
            h[i][1]=h[i-1][1]*r%mod;
        }
        rep(i,0,m+2) {
            LL t=g[i]*g[m+1-i]%mod;
            if (i&1) p3=((p3-h[i][0]*t)%mod+mod)%mod,p4=((p4-h[i][1]*t)%mod+mod)%mod;
            else p3=(p3+h[i][0]*t)%mod,p4=(p4+h[i][1]*t)%mod;
        }
        c=powmod(p4,mod-2)*(mod-p3)%mod;
        rep(i,0,m+2) h[i][0]=(h[i][0]+h[i][1]*c)%mod;
        rep(i,0,m+2) C[i]=h[i][0];
        ans=(calcn(m,C,n)*powmod(R,n)-c)%mod;
        if (ans<0) ans+=mod;
        return ans;
    }
}

LL arr[maxn];
int main(void){__stTIME();__IOPUT();


    int n;
    polysum::init(maxn);
    while(~sci(n)){
        for(int i=1; i<=n; i++) scl(arr[i]);

        sort(arr+1, arr+1+n);

        arr[0] = 0;

        LL now = 1;

        LL b[maxn];

        LL ans = 0;
        for(int i=1; i<=n; i++){
            if(arr[i] == arr[i-1]){
                now = (now * arr[i]) % mod;
                continue;
            }
            b[0] = 0;
            for(int j=1; j<=n-i+1; j++)
                b[j] = (LL)j * ((pow_mod((LL)j, n-i+1) - pow_mod((LL)j-1LL, n-i+1)%mod)+mod)%mod;
            LL tmp = ((polysum::polysum(n-i+1, b, arr[i]+1) -
                       polysum::polysum(n-i+1, b, arr[i-1]+1)%mod)+mod)%mod;

            ans = (ans + (tmp%mod * now%mod)%mod)%mod;

            now = (now * arr[i]) % mod;
        }

        printf("%lld\n", ans);
    }
















__enTIME();return 0;}


void __stTIME()
{
    #if _TIME
        START = clock();
    #endif
}

void __enTIME()
{
    #if _TIME
        END = clock();
        cerr<<"execute time = "<<(double)(END-START)/CLOCKS_PER_SEC<<endl;
    #endif
}

void __IOPUT()
{
    #if _INPUT
        freopen("in.txt", "r", stdin);
    #endif
    #if _OUTPUT
        freopen("out.txt", "w", stdout);
    #endif
}

 

 

注 : 

N + 1 个点能确定一个 N 次多项式、故拉格朗日插值需要确定 ( 最高次次数 + 1 ) 个点的值

 

namespace polysum {
    #define rep(i,a,n) for (int i=a;i<n;i++)
    #define per(i,a,n) for (int i=n-1;i>=a;i--)
    const int D=2010;//可能需要用到的最高次
    LL a[D],f[D],g[D],p[D],p1[D],p2[D],b[D],h[D][2],C[D];
    LL powmod(LL a,LL b){LL res=1;a%=mod;assert(b>=0);for(;b;b>>=1){if(b&1)res=res*a%mod;a=a*a%mod;}return res;}
    LL calcn(int d,LL *a,LL n) { // a[0].. a[d]  a[n]
        if (n<=d) return a[n];
        p1[0]=p2[0]=1;
        rep(i,0,d+1) {
            LL t=(n-i+mod)%mod;
            p1[i+1]=p1[i]*t%mod;
        }
        rep(i,0,d+1) {
            LL t=(n-d+i+mod)%mod;
            p2[i+1]=p2[i]*t%mod;
        }
        LL ans=0;
        rep(i,0,d+1) {
            LL t=g[i]*g[d-i]%mod*p1[i]%mod*p2[d-i]%mod*a[i]%mod;
            if ((d-i)&1) ans=(ans-t+mod)%mod;
            else ans=(ans+t)%mod;
        }
        return ans;
    }
    void init(int M) {//用到的最高次
        f[0]=f[1]=g[0]=g[1]=1;
        rep(i,2,M+5) f[i]=f[i-1]*i%mod;
        g[M+4]=powmod(f[M+4],mod-2);
        per(i,1,M+4) g[i]=g[i+1]*(i+1)%mod;
    }
    LL polysum(LL m,LL *a,LL n) { // a[0].. a[m] \sum_{i=0}^{n-1} a[i]
        for(int i=0;i<=m;i++) b[i]=a[i];
        b[m+1]=calcn(m,b,m+1);
        rep(i,1,m+2) b[i]=(b[i-1]+b[i])%mod;
        return calcn(m+1,b,n-1);
    }
    LL qpolysum(LL R,LL n,LL *a,LL m) { // a[0].. a[m] \sum_{i=0}^{n-1} a[i]*R^i
        if (R==1) return polysum(n,a,m);
        a[m+1]=calcn(m,a,m+1);
        LL r=powmod(R,mod-2),p3=0,p4=0,c,ans;
        h[0][0]=0;h[0][1]=1;
        rep(i,1,m+2) {
            h[i][0]=(h[i-1][0]+a[i-1])*r%mod;
            h[i][1]=h[i-1][1]*r%mod;
        }
        rep(i,0,m+2) {
            LL t=g[i]*g[m+1-i]%mod;
            if (i&1) p3=((p3-h[i][0]*t)%mod+mod)%mod,p4=((p4-h[i][1]*t)%mod+mod)%mod;
            else p3=(p3+h[i][0]*t)%mod,p4=(p4+h[i][1]*t)%mod;
        }
        c=powmod(p4,mod-2)*(mod-p3)%mod;
        rep(i,0,m+2) h[i][0]=(h[i][0]+h[i][1]*c)%mod;
        rep(i,0,m+2) C[i]=h[i][0];
        ans=(calcn(m,C,n)*powmod(R,n)-c)%mod;
        if (ans<0) ans+=mod;
        return ans;
    }
}

 

-------------------------------分 割 线-------------------------------

链接题解用到的化简容斥的多项式展开式如下

( x - 1 ) ^ k

= x^k

+ C(k, 1) * x^(k-1) * (-1)^1

+ C(k, 2) * x^(k-2) * (-1)^2

+ ......

+ C(k, k) * x^(k-k) * (-1)^k