POJ 1161 Walls ( Floyd && 建图 )

题意 : 

在某国，城市之间建起了长城，每一条长城连接两座城市。每条长城互不相交。因此，从一个区域到另一个区域，需要经过一些城镇或者穿过一些长城。任意两个城市A和B之间最多只有一条长城，一端在A城市，另一端在B城市。从A走到B，可以只在一个区域内行走，或者只在长城上行走。

有一个俱乐部，它的会员分布在不同的城市中，每个城市要么只有一个会员，要么没有会员。会员们决定要集中到一个区域内聚会。他们骑车前往目的地。首先，由于城市内交通太堵，他们不想进入任何一个城市内，其次，他们希望穿越尽可能少的长城。他们确定一个聚会的区域之后，有的会员要穿越多条长城才能到达聚会区域，有的会员则可能本身就住在这个区域边上的城市所以不需穿越任何长城。他们希望找到一个区域，使得所有会员穿越长城的数量之和最小。

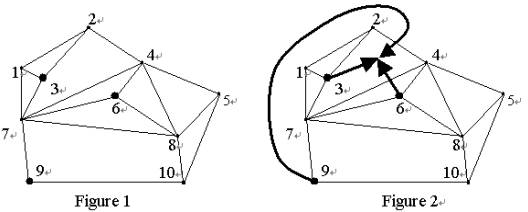
一共有N座城市，城市从1到N编号。如图一所示，有编号的顶点表示城市，每一条边表示一条长城。假设有3个会员，分别住在城市3、6和9，则最佳聚会区域和每个会员的路线如图二所示。共需穿越长城条数是2：城市9的会员需要穿越城市2和城市4之间的长城，城市6的会员需要穿越城市4和7之间的长城。给出城市、区域以及每个会员所在的城市，编一个程序，确定一个最佳的聚会区域，使得需要穿越长城的数量之和最小。

 

分析 :

这题先将各个区域抽象成点，然后每个区域之间如果有边相连 ( 例如题目所给图的 2、4、3、7 和 4、5、8 只通过了一个点相连，所以不算边相连 ) 那么就将这两个区域连接一条边权为 1 的点，然后对于各个城市如果它在某个区域的边缘上，那么就连一条城市到区域点且边权为 0 的有向边 ( 只是为了能让城市和区域之间有相连 )，最后根据这幅图去跑 Floyd 然后枚举区域点作为会员们聚集的点计算贡献取最小即可。这里的判断边相邻的方法，由于图的区域描述是按点顺时针给出（除了最后一个“外部区域”），所以可以根据这个特性，来用点的顺序描述一条边，比如开个数组 info[a][b] = 1 即 a 和 b 相连的边属于区域 1 ，如果下次再碰到有顺序 a、b 的边，那么说明此时这个区域和 1 边相连了，当然在判断的时候 info 里面的顺序是逆序的，而新判断的边是顺序的，至于为什么，模拟一下就知道了！

 

#include<stdio.h>
#include<algorithm>
#include<set>
#include<math.h>
using namespace std;
const int maxn = 500;
const int  INF = 0x3f3f3f3f;
int N, M, L;
int Members[30];
int tmp[maxn];
int info[maxn][maxn];///info[a][b] = c ==> 城市 a、b 之间的边属于区域 c
int dp[maxn][maxn];///跑 Floyd 的邻接矩阵
bool Belong[maxn][maxn];///Belong[a][b] = true ==> 区域 a 包含了点 b，false则反之，一开始初始化为 false

int main(void)
{
    while(~scanf("%d %d %d", &M, &N, &L)){
        for(int i=0; i<L; i++)
            scanf("%d", &Members[i]);

        for(int i=0; i<=M+N; i++){
            for(int j=0; j<=M+N; j++){
                if(i<=N && j<=N) info[i][j] = -1;
                if(i<=N && j<=M) Belong[i][j] = false;
                dp[i][j] = (i==j) ? 0 : INF;
            }
        }


        for(int i=1; i<=M; i++){
            int num;
            scanf("%d", &num);
            for(int j=0; j<num; j++){
                scanf("%d", &tmp[j]);
                Belong[i][tmp[j]] = true;
                //Belong[i].insert(tmp[j]);
                dp[tmp[j]+M][i] = 0; ///连一条城市到这个区域边权为 0 的边
            }

            //if(i == M) std::reverse(tmp, tmp+num);///最后的边是逆序的，一开始没想明白，其实如果倒序了就是错了
            for(int j=0; j<num; j++){
                int & Where = info[tmp[j]][tmp[(j+1)%num]];
                if(Where == -1) info[tmp[(j+1)%num]][tmp[j]] = i;///判断是否有边相连的情况，注意一下正顺和逆序
                else dp[i][Where] = dp[Where][i] = 1;
            }
        }

//        for(int i=1; i<=M+N; i++){
//            for(int j=1; j<=M+N; j++){
//                if(dp[i][j] == INF) printf("x ");
//                else printf("%d ", dp[i][j]);
//            }puts("");
//        }puts("");

        for(int k=1; k<=M+N; k++)
            for(int i=1; i<=M+N; i++)
                for(int j=1; j<=M+N; j++)
                    dp[i][j] = min(dp[i][j], dp[i][k]+dp[k][j]);

        int ans = INF;
        for(int i=1; i<=M; i++){///枚举集合的区域
            int sum = 0;
            for(int j=0; j<L; j++){
                if(Belong[i][Members[j]]) continue;
                sum += dp[Members[j]+M][i];///计算贡献
            }
            ans = min(ans, sum);
        }

        printf("%d\n", ans);
    }
    return 0;
}