UVa 1343 The Rotation Game (状态空间搜索 && IDA*)

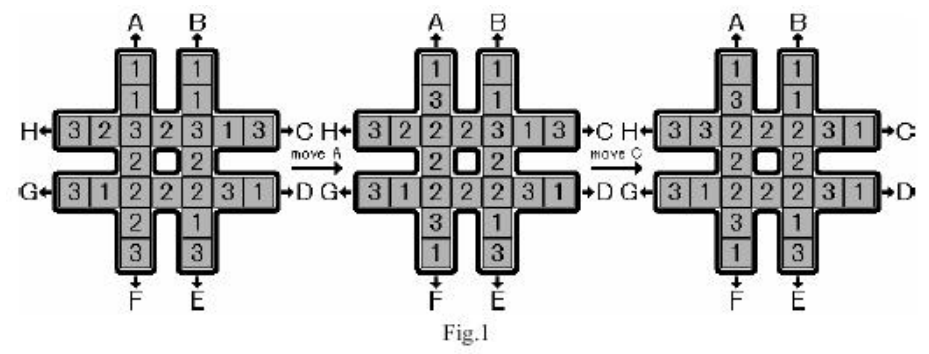
题意：有个＃字型的棋盘，2行2列，一共24个格。

如图：每个格子是1或2或3，一共8个1，8个2，8个3.

有A~H一共8种合法操作，比如A代表把A这一列向上移动一个，最上面的格会补到最下面。

求：使中心8个格子数字一致的最少步骤，要输出具体的操作步骤及最终中心区域的数字。如果有多个解，输出字典序最小的操作步骤。

 

分析 ： 还是状态空间的搜索，对象就是一个数字序列，判断中心位置是否一样，可以看出如果使用BFS，每一层还是爆炸，所以使用IDA*，关键还是模拟操作和h函数，这里的h函数是这样定义的，可以看出每一次操作，最多给当前局面添加一个符合要求的数字，那就统计一下中心区域最多的相同数字有多少，然后如果8-h > max_depth - cur_depth的话代表最好的情况下都无法解决，剪枝。模拟操作应该就是很白痴的数组转移赋值了，代码很长，很烦，建议看看刘汝佳的代码。

#include<bits/stdc++.h>
using namespace std;
int Init[25];
int ans_num;
char ans[1000];
bool Is_ok(int *arr)
{
    int temp = arr[7];
    if(temp!=arr[8] || temp!=arr[9] || temp!=arr[12] || temp!=arr[13] || temp!=arr[16] || temp!=arr[17] || temp!=arr[18])
        return false;
    return true;
}

inline int h(const int *now)
{
    int cnt[4];
    memset(cnt, 0, sizeof(cnt));
    cnt[now[7]]++,  cnt[now[8]]++,  cnt[now[9]]++,
    cnt[now[12]]++, cnt[now[13]]++, cnt[now[16]]++,
    cnt[now[17]]++, cnt[now[18]]++;
    int ret = max(cnt[1], cnt[2]);
    ret = max(ret, cnt[3]);
    return ret;
}

inline void Change(int *tmp, int one, int two, int three, int four, int five, int six, int seven)
{
    int index[9];
    index[1] = one, index[2] = two, index[3] = three,
    index[4] = four, index[5] = five, index[6] = six;
    index[7] = seven;
    int temp = tmp[one];//!
    for(int i=1; i<7; i++)
        tmp[index[i]] = tmp[index[i+1]];
    tmp[index[7]] = temp;
}

bool DFS(int *now, int cur_depth, int max_depth, int per_dir)
{
    if(8 - h(now) > max_depth - cur_depth) return false;
    if(cur_depth >= max_depth) return false;//!?
    for(int dir=1; dir<=8; dir++){//!
        int tmp[25];
        if(per_dir!=0){
            if((per_dir==1&&dir==6) || (dir==1&&per_dir==6)) continue;
            else if((per_dir==2&&dir==5) || (dir==2&&per_dir==5)) continue;
            else if((per_dir==3&&dir==8) || (dir==3&&per_dir==8)) continue;
            else if((per_dir==4&&dir==7) || (dir==4&&per_dir==7)) continue;
        }
        for(int i=1; i<25; i++) tmp[i] = now[i];
        int top = cur_depth;
        switch(dir){
            case 1: ans[top]='A';Change(tmp,1,3,7,12,16,21,23);break;
            case 2: ans[top]='B';Change(tmp,2,4,9,13,18,22,24);break;
            case 3: ans[top]='C';Change(tmp,11,10,9,8,7,6,5);break;
            case 4: ans[top]='D';Change(tmp,20,19,18,17,16,15,14);break;
            case 5: ans[top]='E';Change(tmp,24,22,18,13,9,4,2);break;
            case 6: ans[top]='F';Change(tmp,23,21,16,12,7,3,1);break;
            case 7: ans[top]='G';Change(tmp,14,15,16,17,18,19,20);break;
            case 8: ans[top]='H';Change(tmp,5,6,7,8,9,10,11);break;
        }
        if(Is_ok(tmp)){
            ans[top+1] = '\0';
            ans_num = tmp[7];
            return true;
        }
        if(DFS(tmp, cur_depth+1, max_depth, dir)) return true;
    }
    return false;
}
int main(void)
{
    while(~scanf("%d", &Init[1]) && Init[1]){
        for(int i=2; i<=24; i++){
            scanf("%d", &Init[i]);
        }
        if(Is_ok(Init)){
            puts("No moves needed");
            printf("%d\n", Init[7]);
            continue;
        }
        int max_depth = 1;
        while(1){
            if(DFS(Init, 0, max_depth, 0)) break;
            max_depth++;
        }
        puts(ans);
        printf("%d\n", ans_num);
    }
    return 0;
}

刘汝佳代码：

// UVa1343 The Rotation Game
// Rujia Liu
// This solutions uses IDA* instead of BFS described in the book, because it's shorter 8-)
// It's shorter because no need for lookup tables and "automatically" lexicographically smallest solution.
#include<cstdio>
#include<algorithm>
using namespace std;

/*
      00    01
      02    03
04 05 06 07 08 09 10
      11    12
13 14 15 16 17 18 19
      20    21
      22    23
*/

// lines E~H are computed with the help of rev[]
int line[8][7]={
  { 0, 2, 6,11,15,20,22}, // A
  { 1, 3, 8,12,17,21,23}, // B
  {10, 9, 8, 7, 6, 5, 4}, // C
  {19,18,17,16,15,14,13}, // D
};

const int rev[8] = {5, 4, 7, 6, 1, 0, 3, 2}; // reverse lines of each line

// center squares
const int center[8] = {6, 7, 8, 11, 12, 15, 16, 17};

int a[24];
char ans[1000];

bool is_final() {
  for(int i = 0; i < 8; i++)
    if (a[center[i]] != a[center[0]]) return false;
  return true;
}

int diff(int target) {
  int ans = 0;
  for(int i = 0; i < 8; i++)
    if(a[center[i]] != target) ans++;
  return ans;
}

inline int h() {
  return min(min(diff(1), diff(2)), diff(3));
}

inline void move(int i) {
  int tmp = a[line[i][0]];
  for(int j = 0; j < 6; j++) a[line[i][j]] = a[line[i][j+1]];
  a[line[i][6]] = tmp;
}

bool dfs(int d, int maxd) {
  if(is_final()) {
    ans[d] = '\0';
    printf("%s\n", ans);
    return true;
  }
  if(d + h() > maxd) return false;
  for(int i = 0; i < 8; i++) {
    ans[d] = 'A' + i;
    move(i);
    if(dfs(d+1, maxd)) return true;
    move(rev[i]);
  }
  return false;
}

int main() {
  for(int i = 4; i < 8; i++)
    for(int j = 0; j < 7; j++) line[i][j] = line[rev[i]][6-j];
  while(scanf("%d", &a[0]) == 1 && a[0]) {
    for(int i = 1; i < 24; i++) scanf("%d", &a[i]);
    for(int i = 0; i < 24; i++) if(!a[i]) return 0;
    if(is_final()) {
      printf("No moves needed\n");
    } else {
      for(int maxd = 1; ; maxd++)
        if(dfs(0, maxd)) break;
    }
    printf("%d\n", a[6]);
  }
  return 0;
}

 

瞎：遇到这种看起来很烦的题目，还是没有那种敏感性去试想状态空间搜索，一来就是想着如何模拟，然后脑袋一团shit，思路根本没有，所以总结应该很重要了，提供了一个思考的方向在那里，真正应该思考的是如何去实现这道题所对应的模型，而不是乱想。