「咕咕网校 - 基础省选」树上问题的进阶 by Drench
一定要在noip之前把自己花钱买的Luogu网课梳理完!QAQ
树上前缀和:
对于有根树,在每个点记录 val (点权) 和 sum(到根的点权之和)
当然记录的值因题而异(但是既然叫树上前缀和当然就要这么定义啊)
就可以做一些奇奇怪怪的操作了。
还是看题来理解这玩意儿的妙用吧2333
EG1
给定树和各点点权,t次询问,每次求u到v路径上的点权和。(1e5)
是道板子题了。
从根开始dfs,到每个点时记录该点的val和sum
其中sum为该点到祖先路径上点权之和,包括自己。
每次输出sum[u]+sum[v]-2*sum[lca(u,v)]+val[lca(u,v)]。
EG2
给定初始点权为0的树,n次操作,每次对u,v路径上每点+x。
求最后每点点权。(1e5)
运用差分思想。
对每个点记录一个val值,初始为0。
对于每次操作:
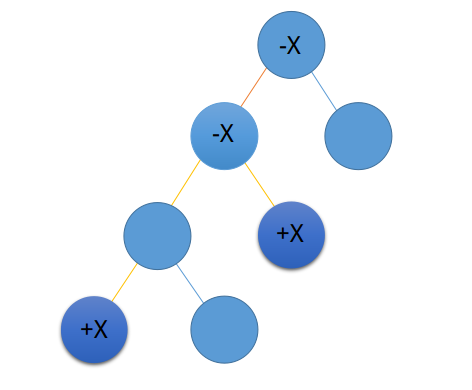
如图,两个深色的是u和v,黄色是u,v的路径。
推一推就会神奇(并不)的发现,每个点的真实点权就是该点的子树点权和。
val[u]+=x; val[v]+=x; val[lca(u,v)]-=x; if(fa[lca(u,v)]!=lca[u,v])
fa[lca(u,v)]-=x;
实现O(4)修改,最后用O(n)得到答案。
“经典的树上差分。”——ddd
EG3
给定树,边有边权。
求有多少对(u,v)使u,v路上所有边的边权异或和为0(1e5)
其中异或和=所有数异或起来的结果
记sum[x]为x到祖先的异或和。
由于异或有:
a xor a = 0
所以如下图,在sum[u] xor sum[v]时,lca以上的屎色线已经被消掉了。
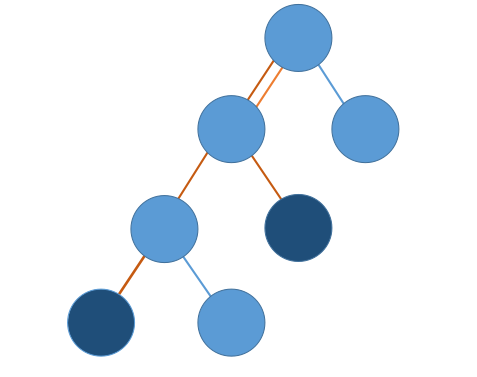
所以ans=sum[u] xor sum[v]
问题转化为:有1e5个数(sum),求中间有多少对数异或和=0
也就是有多少对相等的数。
用一个map记录,然后遍历map就行了。
EG4(留坑
给定一棵N个节点的树,每个点有一个权值val(1e9),对于第M(1e5)个询问(u,v,k),回答u和v这两个节点间第K小的点权。
权值线段树+前缀和。
前置知识:
权值线段树:以val为下标的树。
EG:
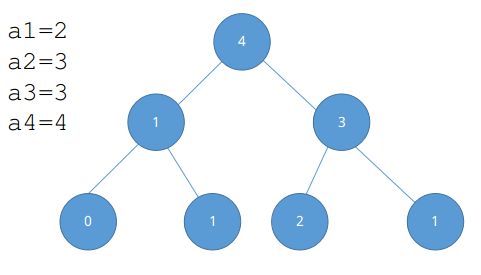
对于序列版本(在序列上问l到r之间第k大的数):
每加入一个新的点,只会对权值线段树上的logn个点产生影响。
所以从左往右每加入一个新点,就可持久化一下。
对于每个询问,算出[1,l-1]的权值线段树和[l,r]的权值线段树,减一下就星了。
(以下照抄ppt)
“对于树上版本,每个点从其父亲的版本可持久化而来。
那么对于一条路径,和树上前缀和一样,由4棵线段树即可提取出这条路径表示的权值线段树。
再在线段树上查询即可。”
好像还要四个主席树怎么搞一搞吧2333
我连可持久化都不会你跟我说这些东西?!!
DFS序
此物如名,就是dfs的顺序。
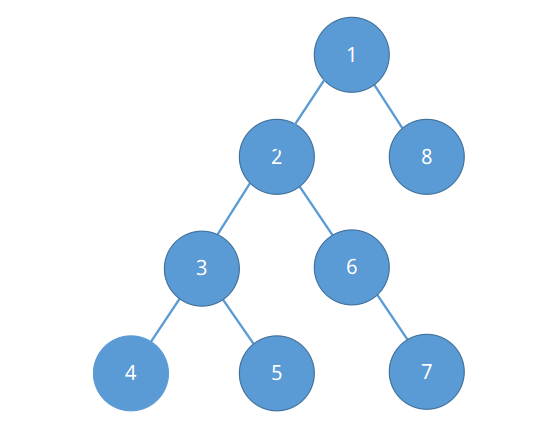
如图,如果按照前序遍历(根->左->右)去搜的话,搜索序就会是这样。
搜索的方法可以 根左右 可以 根右左 ,记录也有 只在进入时记一次 和 进入弹出都记 啊什么的,大同小异。
对于我们现在讨论的这种dfs序,有这样一个神奇的性质:
一个树的子树中的点,在dfs序上是连续的。
换言之,设该点为i,它在dfs序上的位置为pos,子树大小为siz。
则它的子树中的点在[pos,pos+siz-1]上。
这玩意儿我们可以联系代码解释:
1 void dfsx(int x) 2 { 3 cout<<x<<" "; 4 for(int i=heap[x];i;i=a[i].next) 5 { 6 dfsx(a[i].to); 7 } 8 return; 9 }
差不多是这样,想一想就能通了(吧)
EG
给定一棵有n个节点的树。 有两种操作: 1.给u的子树上每点+v 2.求u的子树上的点权和(1e5)
是道板子题了。
根据我们之前搞出来的dfs序,可以把对子树的操作转化为区间问题(区间加 区间求和)
然后线段树就行了。
以及dfs序还在LCA的ST法上有用,多年前的ST学习笔记。
树链剖分(轻重链剖分)
对于一个点,我们记它的所有儿子中,子树最大的一个儿子为重儿子,连接该儿子的边为重边(深色边);否则为轻边。
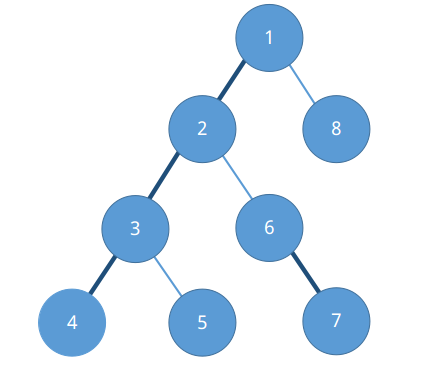
如图。
性质:从根到某一点的路径上,有不超过logn条轻边,不超过logn条重边。
代码实现方面:(口胡ing 等我口胡完就代码实现
首先扫一遍,得到哪些点是重儿子->哪些边是重边
然后对每个点,记fa[x]为x的父节点,top[x]为x在只走重链的前提下的祖先
恭喜你得到了一棵剖好了的树!
LCA(1e5)
对于u,v:
若top[u]==top[v],则lca为u,v中深度较小的那个点;
否则把链头较深的点 跳到链头的父亲处。
本质上还是算暴力跳的鬼畜优化吧(挠头
LA(一个点向上x步的祖先)(1e5)
对于查询u向上x步: 设当前点dep[u],目标祖先的dep就是dep[u]-x; 如果top[u]的dep比目标dep深,那么跳到链头的父亲处;(logn) 否则: 目标点肯定在当前点到top的路上。 也就是在这条重链上,所以在dfs序上连续。 从而所求点的dfn就是 top的dfn 加上 它到top的dep差。O(1)
EG6
树剖模板。
EG7
给定树,有点权。
操作:1.从u到v路径上每点点权+t
2.求所有于u点相邻的点的点权和
记每个点的轻儿子之和为sum[x]。
对于每次修改,暴力做轻儿子(树剖嘛)
每次查询该点的sum和重儿子和fa。
换根意义下的操作
————to be continued


