求一维数组的最大子数组1(结对开发)

题目：返回一个整数数组中最大子数组的和。

要求：

输入一个整形数组，数组里有正数也有负数。

数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。

求所有子数组的和的最大值。要求时间复杂度为O(n)

发表一篇博客文章讲述设计思想，出现的问题，可能的解决方案（多选）、源代码、结果截图、总结。

 

结对开发的伙伴：

博客名：Mr.缪

姓名：缪金敏

链接：http://www.cnblogs.com/miaojinmin799/

分析：

如果按照最笨的方法就是一个一个的比较先比较一个数的然后二个，直到个数为n为止，但是这样时间复杂度一算估计得要O(n*n)，所以不可行，后来通过上网查阅，找到了动态规划方法来实现求最大和，把比较大小分解为一小段一小段，每次比较输入数和输入前几个数之和的大小，选择最大的。要想输出子数组，就必须判断开始下标和结束下标。开始下标的条件：数组第二列的数前一个比现在的小且小于0且第一列的数小于等于第二列。结束下标的条件：当前的算出的最大子数组+输入的值比下一步的最大值大于或等于，或第二列的数大于等于第一列。

所遇到困难：

开始下标和结束下标考虑过于单一，有些特殊情况没有考虑到。

结对开发照：

源代码：

//求一维数组的最大子数组 王文奇 缪金敏 2016/3/23
#include<iostream>
using namespace std;

int max(int a,int b)   //返回a和b中的最大值
{
    if (a > b)
    {
        return a;
    }
    else
    {
        return b;
    }
}

int main()
{
        int Array[100];
        int i = 1;
        int dynamic_planning[100][2], j, sum;
        int start = 0;                   //最大子数组的起始位置  
        int end = 0;                    //最大子数组的终止位置  
        cout << "请输入一组一维数组(回车结束)："<<endl;
        cin >> Array[0];
        while (cin.get() != '\n') //回车结束
        {
            cin >> Array[i++];
        }
        //动态规划数组初始化
        dynamic_planning[0][0] = 0;
        dynamic_planning[0][1] = Array[0];
        for (j = 1; j<i; j++)
        {
            dynamic_planning[j][0] = max(dynamic_planning[j - 1][0], dynamic_planning[j - 1][1]);
            dynamic_planning[j][1] = max(Array[j], (dynamic_planning[j - 1][1] + Array[j]));
            //开始下标的条件：数组第二列的数前一个比现在的小且小于0且第一列的数小于等于第二列
            if (dynamic_planning[j - 1][1] < dynamic_planning[j][1] && dynamic_planning[j - 1][1]<0&&dynamic_planning[j][0]<=dynamic_planning[j][1])
            { 
                start = j;
                //cout << "start:"<<start << endl;
            }
            //结束下标的条件1：当前的算出的最大子数组+输入的值比下一步的最大值大于或等于
            if (dynamic_planning[j - 1][1] >= dynamic_planning[j][0])
            {
                end = j - 1;
                //cout << "end:" << end << endl;
            }
            //结束下标的条件2：第二列的数大于等于第一列
            if (dynamic_planning[j][1] >= dynamic_planning[j][0])
            {
                end = j;
                //cout << "end:" << end << endl;
            }
            
        }
        //cout << start << " " << end << endl;
        sum = max(dynamic_planning[i - 1][0], dynamic_planning[i - 1][1]);
        cout << "最大的子数组为：" << endl;
         for (int i = start; i <= end; i++)
         {
             cout << Array[i] << " ";
         } 
         cout << endl;
         cout << "最大的子数组的和为：" << sum << endl;
        return 0;
}

运行结果截图：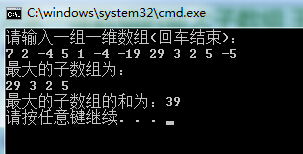

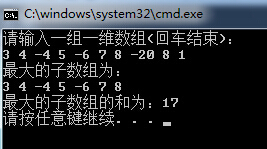
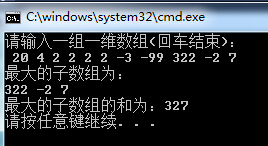
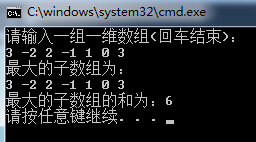
总结：

      这次实验主要运用了动态规划的思想，再就是临界下标的判断，一定考虑到所有的情况。

项目计划总结：

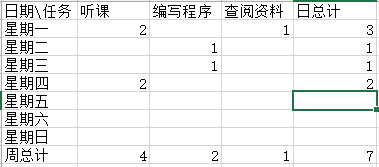
时间记入日志：

缺陷记入日志：