图像处理8 选择性搜索(selective search)
介绍
以下介绍和算法引用自选择性搜索(selective search)。
一、目标检测 VS 目标识别
目标识别(objec recognition)是指明一幅输入图像中包含那类目标。其输入为一幅图像,输出是该图像中的目标属于哪个类别(class probability)。而目标检测(object detection)除了要告诉输入图像中包含了哪类目前外,还要框出该目标的具体位置(bounding boxes)。
在目标检测时,为了定位到目标的具体位置,通常会把图像分成许多子块(sub-regions / patches),然后把子块作为输入,送到目标识别的模型中。分子块的最直接方法叫滑动窗口法(sliding window approach)。滑动窗口的方法就是按照子块的大小在整幅图像上穷举所有子图像块。这种方法产生的数据量想想都头大。和滑动窗口法相对的是另外一类基于区域(region proposal)的方法。selective search就是其中之一!
二、selective search算法流程
step0:生成区域集R,具体参见论文《Efficient Graph-Based Image Segmentation》
step1:计算区域集R里每个相邻区域的相似度S={s1,s2,…}
step2:找出相似度最高的两个区域,将其合并为新集,添加进R
step3:从S中移除所有与step2中有关的子集
step4:计算新集与所有子集的相似度
step5:跳至step2,直至S为空三、相似度计算
论文考虑了颜色、纹理、尺寸和空间交叠这4个参数。
3.1、颜色相似度(color similarity)
将色彩空间转为HSV,每个通道下以bins=25计算直方图,这样每个区域的颜色直方图有25*3=75个区间。 对直方图除以区域尺寸做归一化后使用下式计算相似度:
3.2、纹理相似度(texture similarity)
论文采用方差为1的高斯分布在8个方向做梯度统计,然后将统计结果(尺寸与区域大小一致)以bins=10计算直方图。直方图区间数为8*3*10=240(使用RGB色彩空间)。
其中,
是直方图中第
个bin的值。
3.3、尺寸相似度(size similarity)
保证合并操作的尺度较为均匀,避免一个大区域陆续“吃掉”其他小区域。
例:设有区域a-b-c-d-e-f-g-h。较好的合并方式是:ab-cd-ef-gh -> abcd-efgh -> abcdefgh。 不好的合并方法是:ab-c-d-e-f-g-h ->abcd-e-f-g-h ->abcdef-gh -> abcdefgh。
3.4、交叠相似度(shape compatibility measure)
3.5、最终的相似度
实现
使用了前面几篇提到的一些算法,运行速度慢
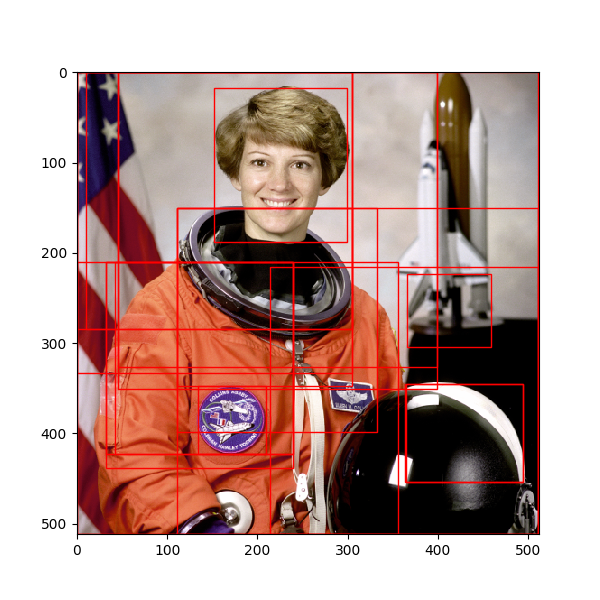
# -*- coding: utf-8 -*- from __future__ import division from skimage.color import rgb2hsv from skimage.data import astronaut import numpy from _felzenszwalb_cy import _felzenszwalb_cython import matplotlib.patches as mpatches import matplotlib.pyplot as plt import math # "Selective Search for Object Recognition" by J.R.R. Uijlings et al. # # - Modified version with LBP extractor for texture vectorization def _sim_colour(r1, r2): """ calculate the sum of histogram intersection of colour """ return sum([min(a, b) for a, b in zip(r1["hist_c"], r2["hist_c"])]) def _sim_texture(r1, r2): """ calculate the sum of histogram intersection of texture """ return sum([min(a, b) for a, b in zip(r1["hist_t"], r2["hist_t"])]) def _sim_size(r1, r2, imsize): """ calculate the size similarity over the image """ return 1.0 - (r1["size"] + r2["size"]) / imsize def _sim_fill(r1, r2, imsize): """ calculate the fill similarity over the image """ bbsize = ( (max(r1["max_x"], r2["max_x"]) - min(r1["min_x"], r2["min_x"])) * (max(r1["max_y"], r2["max_y"]) - min(r1["min_y"], r2["min_y"])) ) return 1.0 - (bbsize - r1["size"] - r2["size"]) / imsize def _calc_sim(r1, r2, imsize): return (_sim_colour(r1, r2) + _sim_texture(r1, r2) + _sim_size(r1, r2, imsize) + _sim_fill(r1, r2, imsize)) def histogram(a, bins=10, range=None): """ Compute the histogram of a set of data. """ import numpy as numpy from numpy.core import linspace from numpy.core.numeric import (arange, asarray) # 转成一维数组 a = asarray(a) a = a.ravel() mn, mx = [mi + 0.0 for mi in range] ntype = numpy.dtype(numpy.intp) n = numpy.zeros(bins, ntype) # 预计算直方图缩放因子 norm = bins / (mx - mn) # 均分,计算边缘以进行潜在的校正 bin_edges = linspace(mn, mx, bins + 1, endpoint=True) # 分块对于大数组可以降低运行内存,同时提高速度 BLOCK = 65536 for i in arange(0, len(a), BLOCK): tmp_a = a[i:i + BLOCK] tmp_a_data = tmp_a.astype(float) # 减去Range下限,乘以缩放因子,向下取整 tmp_a = tmp_a_data - mn tmp_a *= norm indices = tmp_a.astype(numpy.intp) # 对indices标签分别计数,标签等于bins减一 indices[indices == bins] -= 1 n += numpy.bincount(indices, weights=None, minlength=bins).astype(ntype) return n, bin_edges def _calc_colour_hist(img): """ calculate colour histogram for each region the size of output histogram will be BINS * COLOUR_CHANNELS(3) number of bins is 25 as same as [uijlings_ijcv2013_draft.pdf] extract HSV """ BINS = 25 hist = numpy.array([]) for colour_channel in (0, 1, 2): # extracting one colour channel c = img[:, colour_channel] # calculate histogram for each colour and join to the result hist = numpy.concatenate( [hist] + [histogram(c, BINS, (0.0, 255.0))[0]]) # L1 normalize hist = hist / len(img) return hist def circular_LBP(src, n_points, radius): height = src.shape[0] width = src.shape[1] dst = src.copy() src.astype(dtype=numpy.float32) dst.astype(dtype=numpy.float32) neighbours = numpy.zeros((1, n_points), dtype=numpy.uint8) lbp_value = numpy.zeros((1, n_points), dtype=numpy.uint8) for x in range(radius, width - radius - 1): for y in range(radius, height - radius - 1): lbp = 0. # 先计算共n_points个点对应的像素值,使用双线性插值法 for n in range(n_points): theta = float(2 * numpy.pi * n) / n_points x_n = x + radius * numpy.cos(theta) y_n = y - radius * numpy.sin(theta) # 向下取整 x1 = int(math.floor(x_n)) y1 = int(math.floor(y_n)) # 向上取整 x2 = int(math.ceil(x_n)) y2 = int(math.ceil(y_n)) # 将坐标映射到0-1之间 tx = numpy.abs(x - x1) ty = numpy.abs(y - y1) # 根据0-1之间的x,y的权重计算公式计算权重 w1 = (1 - tx) * (1 - ty) w2 = tx * (1 - ty) w3 = (1 - tx) * ty w4 = tx * ty # 根据双线性插值公式计算第k个采样点的灰度值 neighbour = src[y1, x1] * w1 + src[y2, x1] * w2 + src[y1, x2] * w3 + src[y2, x2] * w4 neighbours[0, n] = neighbour center = src[y, x] for n in range(n_points): if neighbours[0, n] > center: lbp_value[0, n] = 1 else: lbp_value[0, n] = 0 for n in range(n_points): lbp += lbp_value[0, n] * 2**n # 转换到0-255的灰度空间,比如n_points=16位时结果会超出这个范围,对该结果归一化 dst[y, x] = int(lbp / (2**n_points-1) * 255) return dst def _calc_texture_gradient(img): """ calculate texture gradient for entire image The original SelectiveSearch algorithm proposed Gaussian derivative for 8 orientations, but we use LBP instead. output will be [height(*)][width(*)] """ ret = numpy.zeros((img.shape[0], img.shape[1], img.shape[2])) for colour_channel in (0, 1, 2): ret[:, :, colour_channel] = circular_LBP( img[:, :, colour_channel], 8, 1) return ret def _calc_texture_hist(img): """ calculate texture histogram for each region calculate the histogram of gradient for each colours the size of output histogram will be BINS * ORIENTATIONS * COLOUR_CHANNELS(3) """ BINS = 10 hist = numpy.array([]) for colour_channel in (0, 1, 2): # mask by the colour channel fd = img[:, colour_channel] # calculate histogram for each orientation and concatenate them all # and join to the result hist = numpy.concatenate( [hist] + [numpy.histogram(fd, BINS, (0.0, 1.0))[0]]) # L1 Normalize hist = hist / len(img) return hist def _merge_regions(r1, r2): new_size = r1["size"] + r2["size"] rt = { "min_x": min(r1["min_x"], r2["min_x"]), "min_y": min(r1["min_y"], r2["min_y"]), "max_x": max(r1["max_x"], r2["max_x"]), "max_y": max(r1["max_y"], r2["max_y"]), "size": new_size, "hist_c": ( r1["hist_c"] * r1["size"] + r2["hist_c"] * r2["size"]) / new_size, "hist_t": ( r1["hist_t"] * r1["size"] + r2["hist_t"] * r2["size"]) / new_size, "labels": r1["labels"] + r2["labels"] } return rt def selective_search( im_orig, scale=1.0, sigma=0.8, min_size=50): assert im_orig.shape[2] == 3, "3ch image is expected" # 加载图像,使用felzenszwalb算法获取候选区域,区域标签存储到数据的第四维 im_mask = _felzenszwalb_cython( im_orig, scale=scale, sigma=sigma, min_size=min_size, kernel=9) img = numpy.append( im_orig, numpy.zeros(im_orig.shape[:2])[:, :, numpy.newaxis], axis=2) img[:, :, 3] = im_mask if img is None: return None, {} imsize = img.shape[0] * img.shape[1] R = {} hsv = rgb2hsv(img[:, :, :3]) # 第一步: 存储像素位置 for y, i in enumerate(img): for x, (r, g, b, l) in enumerate(i): # 新区域 if l not in R: R[l] = { "min_x": 0xffff, "min_y": 0xffff, "max_x": 0, "max_y": 0, "labels": [l]} # bounding box if R[l]["min_x"] > x: R[l]["min_x"] = x if R[l]["min_y"] > y: R[l]["min_y"] = y if R[l]["max_x"] < x: R[l]["max_x"] = x if R[l]["max_y"] < y: R[l]["max_y"] = y # 第二步: 计算LBP纹理特征 tex_grad = _calc_texture_gradient(img) # 第三步: 计算每个区域的颜色直方图 for k, v in list(R.items()): masked_pixels = hsv[:, :, :][img[:, :, 3] == k] R[k]["size"] = len(masked_pixels) # /4 R[k]["hist_c"] = _calc_colour_hist(masked_pixels) R[k]["hist_t"] = _calc_texture_hist(tex_grad[:, :][img[:, :, 3] == k]) # 提取邻域信息 def intersect(a, b): if (a["min_x"] < b["min_x"] < a["max_x"] and a["min_y"] < b["min_y"] < a["max_y"]) or ( a["min_x"] < b["max_x"] < a["max_x"] and a["min_y"] < b["max_y"] < a["max_y"]) or ( a["min_x"] < b["min_x"] < a["max_x"] and a["min_y"] < b["max_y"] < a["max_y"]) or ( a["min_x"] < b["max_x"] < a["max_x"] and a["min_y"] < b["min_y"] < a["max_y"]): return True return False R_list = list(R.items()) neighbours = [] for cur, a in enumerate(R_list[:-1]): for b in R_list[cur + 1:]: if intersect(a[1], b[1]): neighbours.append((a, b)) # 计算初始相似度 S = {} for (ai, ar), (bi, br) in neighbours: S[(ai, bi)] = _calc_sim(ar, br, imsize) # hierarchal search while S != {}: # get highest similarity i, j = sorted(S.items(), key=lambda i: i[1])[-1][0] # merge corresponding regions t = max(R.keys()) + 1.0 R[t] = _merge_regions(R[i], R[j]) # mark similarities for regions to be removed key_to_delete = [] for k, v in list(S.items()): if (i in k) or (j in k): key_to_delete.append(k) # remove old similarities of related regions for k in key_to_delete: del S[k] # calculate similarity set with the new region for k in [a for a in key_to_delete if a != (i, j)]: n = k[1] if k[0] in (i, j) else k[0] S[(t, n)] = _calc_sim(R[t], R[n], imsize) regions = [] for k, r in list(R.items()): regions.append({ 'rect': ( r['min_x'], r['min_y'], r['max_x'] - r['min_x'], r['max_y'] - r['min_y']), 'size': r['size'], 'labels': r['labels'] }) return img, regions if __name__=="__main__": img = astronaut() # perform selective search img_lbl, regions = selective_search( img, scale=500, sigma=0.9, min_size=10) candidates = set() for r in regions: # excluding same rectangle (with different segments) if r['rect'] in candidates: continue # excluding regions smaller than 2000 pixels if r['size'] < 2000: continue # distorted rects x, y, w, h = r['rect'] if w / h > 1.2 or h / w > 1.2: continue candidates.add(r['rect']) # draw rectangles on the original image fig, ax = plt.subplots(ncols=1, nrows=1, figsize=(6, 6)) ax.imshow(img) for x, y, w, h in candidates: print(x, y, w, h) rect = mpatches.Rectangle( (x, y), w, h, fill=False, edgecolor='red', linewidth=1) ax.add_patch(rect) plt.show() """ (46, 0, 353, 326) (366, 223, 93, 81) (365, 345, 129, 109) (32, 210, 207, 213) (10, 0, 295, 284) (0, 0, 305, 284) (152, 17, 147, 171) (32, 210, 207, 228) (111, 150, 400, 361) (0, 210, 356, 301) (42, 210, 197, 213) (0, 0, 305, 333) (0, 0, 511, 511) (111, 150, 194, 198) (134, 348, 75, 75) (46, 0, 353, 351) (111, 150, 221, 248) (214, 216, 297, 295) (364, 345, 130, 109) """
_felzenszwalb_cython代码如下。
import numpy as np import cv2 def find_root(forest, n): """Find the root of node n. Given the example above, for any integer from 1 to 9, 1 is always returned """ root = n while (forest[root] < root): root = forest[root] return root def set_root(forest, n, root): """ Set all nodes on a path to point to new_root. Given the example above, given n=9, root=6, it would "reconnect" the tree. so forest[9] = 6 and forest[8] = 6 The ultimate goal is that all tree nodes point to the real root, which is element 1 in this case. """ while (forest[n] < n): j = forest[n] forest[n] = root n = j forest[n] = root def join_trees(forest, n, m): """Join two trees containing nodes n and m. If we imagine that in the example tree, the root 1 is not known, we rather have two disjoint trees with roots 2 and 6. Joining them would mean that all elements of both trees become connected to the element 2, so forest[9] == 2, forest[6] == 2 etc. However, when the relationship between 1 and 2 can still be discovered later. """ if (n != m): root = find_root(forest, n) root_m = find_root(forest, m) if (root > root_m): root = root_m set_root(forest, n, root) set_root(forest, m, root) def _felzenszwalb_cython(image, scale=1, sigma=0.8,kernel=3,min_size=20): """Felzenszwalb's efficient graph based segmentation for single or multiple channels. Produces an oversegmentation of a single or multi-channel image using a fast, minimum spanning tree based clustering on the image grid. The number of produced segments as well as their size can only be controlled indirectly through ``scale``. Segment size within an image can vary greatly depending on local contrast. Parameters ---------- image : (N, M, C) ndarray Input image. scale : float, optional (default 1) Sets the obervation level. Higher means larger clusters. sigma : float, optional (default 0.8) Width of Gaussian smoothing kernel used in preprocessing. Larger sigma gives smother segment boundaries. min_size : int, optional (default 20) Minimum component size. Enforced using postprocessing. Returns ------- segment_mask : (N, M) ndarray Integer mask indicating segment labels. """ # image = img_as_float(image) image = np.asanyarray(image, dtype=np.float) / 255 # rescale scale to behave like in reference implementation scale = float(scale) / 255. # image = ndi.gaussian_filter(image, sigma=[sigma, sigma, 0]) image =cv2.GaussianBlur(image, (kernel, kernel), sigma) # compute edge weights in 8 connectivity: down_cost = np.sqrt(np.sum((image[1:, :, :] - image[:-1, :, :]) *(image[1:, :, :] - image[:-1, :, :]), axis=-1)) right_cost = np.sqrt(np.sum((image[:, 1:, :] - image[:, :-1, :]) *(image[:, 1:, :] - image[:, :-1, :]), axis=-1)) dright_cost = np.sqrt(np.sum((image[1:, 1:, :] - image[:-1, :-1, :]) *(image[1:, 1:, :] - image[:-1, :-1, :]), axis=-1)) uright_cost = np.sqrt(np.sum((image[1:, :-1, :] - image[:-1, 1:, :]) *(image[1:, :-1, :] - image[:-1, 1:, :]), axis=-1)) costs = np.hstack([ right_cost.ravel(), down_cost.ravel(), dright_cost.ravel(), uright_cost.ravel()]).astype(np.float) # compute edges between pixels: height, width = image.shape[:2] segments = np.arange(width * height, dtype=np.intp).reshape(height, width) down_edges = np.c_[segments[1:, :].ravel(), segments[:-1, :].ravel()] right_edges = np.c_[segments[:, 1:].ravel(), segments[:, :-1].ravel()] dright_edges = np.c_[segments[1:, 1:].ravel(), segments[:-1, :-1].ravel()] uright_edges = np.c_[segments[:-1, 1:].ravel(), segments[1:, :-1].ravel()] edges = np.vstack([right_edges, down_edges, dright_edges, uright_edges]) # initialize data structures for segment size # and inner cost, then start greedy iteration over edges. edge_queue = np.argsort(costs) edges = np.ascontiguousarray(edges[edge_queue]) costs = np.ascontiguousarray(costs[edge_queue]) segments_p = np.arange(width * height, dtype=np.intp) #segments segment_size = np.ones(width * height, dtype=np.intp) # inner cost of segments cint = np.zeros(width * height) num_costs = costs.size for e in range(num_costs): seg0 = find_root(segments_p, edges[e][0]) seg1 = find_root(segments_p, edges[e][1]) if seg0 == seg1: continue inner_cost0 = cint[seg0] + scale / segment_size[seg0] inner_cost1 = cint[seg1] + scale / segment_size[seg1] if costs[e] < min(inner_cost0, inner_cost1): # update size and cost join_trees(segments_p, seg0, seg1) seg_new = find_root(segments_p, seg0) segment_size[seg_new] = segment_size[seg0] + segment_size[seg1] cint[seg_new] = costs[e] # postprocessing to remove small segments # edges = edges for e in range(num_costs): seg0 = find_root(segments_p, edges[e][0]) seg1 = find_root(segments_p, edges[e][1]) if seg0 == seg1: continue if segment_size[seg0] < min_size or segment_size[seg1] < min_size: join_trees(segments_p, seg0, seg1) seg_new = find_root(segments_p, seg0) segment_size[seg_new] = segment_size[seg0] + segment_size[seg1] # unravel the union find tree flat = segments_p.ravel() old = np.zeros_like(flat) while (old != flat).any(): old = flat flat = flat[flat] flat = np.unique(flat, return_inverse=True)[1] return flat.reshape((height, width))



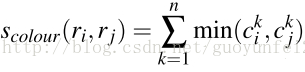








【推荐】还在用 ECharts 开发大屏?试试这款永久免费的开源 BI 工具!
【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步