图像处理7 LBP纹理特征提取
LBP纹理特征提取
LBP(Local Binary Pattern,局部二值模式)是一种用来描述图像局部纹理特征的算子;它具有旋转不变性和灰度不变性等显著的优点。它是首先由T. Ojala, M.Pietikäinen,和 D. Harwood 在1994年提出,用于纹理特征提取。而且,提取的特征是图像的局部的纹理特征;
1、LBP特征的描述
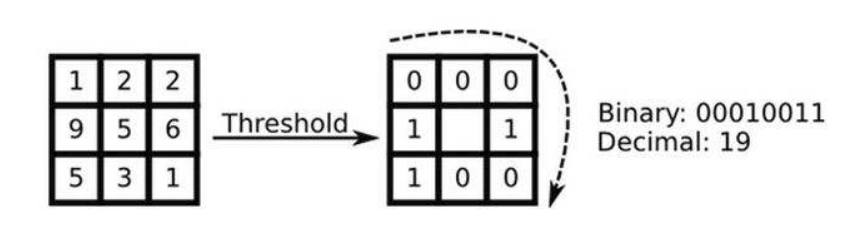
原始的LBP算子定义为在3*3的窗口内,以窗口中心像素为阈值,将相邻的8个像素的灰度值与其进行比较,若周围像素值大于中心像素值,则该像素点的位置被标记为1,否则为0。这样,3*3邻域内的8个点经比较可产生8位二进制数(通常转换为十进制数即LBP码,共256种),即得到该窗口中心像素点的LBP值,并用这个值来反映该区域的纹理信息。如下图所示:
LBP的改进版本:
原始的LBP提出后,研究人员不断对其提出了各种改进和优化。
(1)圆形LBP算子:
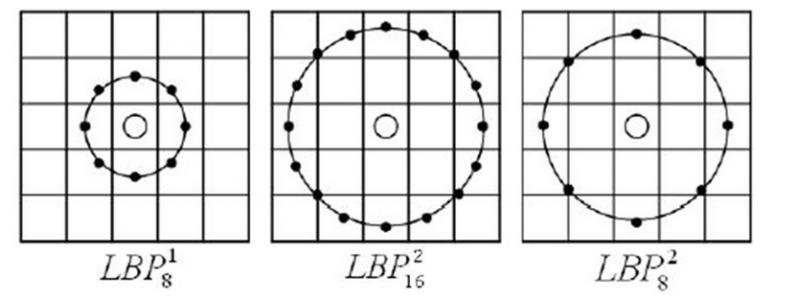
基本的 LBP算子的最大缺陷在于它只覆盖了一个固定半径范围内的小区域,这显然不能满足不同尺寸和频率纹理的需要。为了适应不同尺度的纹理特征,并达到灰度和旋转不变性的要求,Ojala等对 LBP算子进行了改进,将 3×3邻域扩展到任意邻域,并用圆形邻域代替了正方形邻域,改进后的 LBP算子允许在半径为 R 的圆形邻域内有任意多个像素点。从而得到了诸如半径为R的圆形区域内含有P个采样点的LBP算子;
(2)LBP旋转不变模式
从 LBP 的定义可以看出,LBP 算子是灰度不变的,但却不是旋转不变的。图像的旋转就会得到不同的 LBP值。
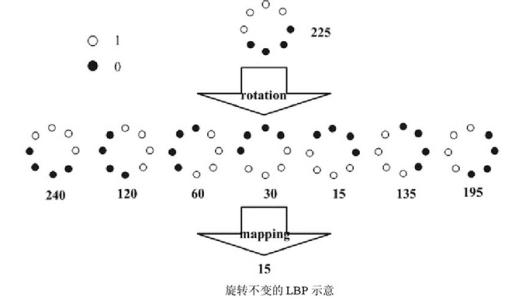
Maenpaa等人又将 LBP算子进行了扩展,提出了具有旋转不变性的 LBP算子,即不断旋转圆形邻域得到一系列初始定义的 LBP值,取其最小值作为该邻域的 LBP值。
上图给出了求取旋转不变的 LBP 的过程示意图,图中算子下方的数字表示该算子对应的 LBP值,图中所示的 8种 LBP模式,经过旋转不变的处理,最终得到的具有旋转不变性的 LBP值为 15。也就是说,图中的 8种 LBP 模式对应的旋转不变的 LBP模式都是 00001111。
(3)LBP等价模式
一个LBP算子可以产生不同的二进制模式,对于半径为R的圆形区域内含有P个采样点的LBP算子将会产生P2种模式。很显然,随着邻域集内采样点数的增加,二进制模式的种类是急剧增加的。例如:5×5邻域内20个采样点,有220=1,048,576种二进制模式。如此多的二值模式无论对于纹理的提取还是对于纹理的识别、分类及信息的存取都是不利的。同时,过多的模式种类对于纹理的表达是不利的。例如,将LBP算子用于纹理分类或人脸识别时,常采用LBP模式的统计直方图来表达图像的信息,而较多的模式种类将使得数据量过大,且直方图过于稀疏。因此,需要对原始的LBP模式进行降维,使得数据量减少的情况下能最好的代表图像的信息。
为了解决二进制模式过多的问题,提高统计性,Ojala提出了采用一种“等价模式”(Uniform Pattern)来对LBP算子的模式种类进行降维。Ojala等认为,在实际图像中,绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变。因此,Ojala将“等价模式”定义为:当某个LBP所对应的循环二进制数从0到1或从1到0最多有两次跳变时,该LBP所对应的二进制就称为一个等价模式类。如00000000(0次跳变),00000111(只含一次从0到1的跳变),10001111(先由1跳到0,再由0跳到1,共两次跳变)都是等价模式类。除等价模式类以外的模式都归为另一类,称为混合模式类,例如10010111(共四次跳变)(这是我的个人理解,不知道对不对)。
通过这样的改进,二进制模式的种类大大减少,而不会丢失任何信息。模式数量由原来的2P种减少为 P ( P-1)+2种,其中P表示邻域集内的采样点数。对于3×3邻域内8个采样点来说,二进制模式由原始的256种减少为58种,这使得特征向量的维数更少,并且可以减少高频噪声带来的影响。
2、LBP特征用于检测的原理
显而易见的是,上述提取的LBP算子在每个像素点都可以得到一个LBP“编码”,那么,对一幅图像(记录的是每个像素点的灰度值)提取其原始的LBP算子之后,得到的原始LBP特征依然是“一幅图片”(记录的是每个像素点的LBP值)。
LBP的应用中,如纹理分类、人脸分析等,一般都不将LBP图谱作为特征向量用于分类识别,而是采用LBP特征谱的统计直方图作为特征向量用于分类识别。
因为,从上面的分析我们可以看出,这个“特征”跟位置信息是紧密相关的。直接对两幅图片提取这种“特征”,并进行判别分析的话,会因为“位置没有对准”而产生很大的误差。后来,研究人员发现,可以将一幅图片划分为若干的子区域,对每个子区域内的每个像素点都提取LBP特征,然后,在每个子区域内建立LBP特征的统计直方图。如此一来,每个子区域,就可以用一个统计直方图来进行描述;整个图片就由若干个统计直方图组成;
例如:一幅100*100像素大小的图片,划分为10*10=100个子区域(可以通过多种方式来划分区域),每个子区域的大小为10*10像素;在每个子区域内的每个像素点,提取其LBP特征,然后,建立统计直方图;这样,这幅图片就有10*10个子区域,也就有了10*10个统计直方图,利用这10*10个统计直方图,就可以描述这幅图片了。之后,我们利用各种相似性度量函数,就可以判断两幅图像之间的相似性了;
3、对LBP特征向量进行提取的步骤
(1)首先将检测窗口划分为16×16的小区域(cell);
(2)对于每个cell中的一个像素,将相邻的8个像素的灰度值与其进行比较,若周围像素值大于中心像素值,则该像素点的位置被标记为1,否则为0。这样,3*3邻域内的8个点经比较可产生8位二进制数,即得到该窗口中心像素点的LBP值;
(3)然后计算每个cell的直方图,即每个数字(假定是十进制数LBP值)出现的频率;然后对该直方图进行归一化处理。
(4)最后将得到的每个cell的统计直方图进行连接成为一个特征向量,也就是整幅图的LBP纹理特征向量;
公式和实现(以圆形LBP为例)
原始LBP公式

圆形LBP公式

Python代码
包含从scikit-image源码简化的local_binary_pattern和根据公式实现的圆形LBP,结果一致。
# coding: utf8 from __future__ import division import numpy as np import math import matplotlib.pyplot as plt from skimage.data import coffee def local_binary_pattern(image, P, R): """Gray scale and rotation invariant LBP (Local Binary Patterns). LBP is an invariant descriptor that can be used for texture classification. """ # local position of texture elements rr = - R * np.sin(2 * np.pi * np.arange(P, dtype=np.double) / P) cc = R * np.cos(2 * np.pi * np.arange(P, dtype=np.double) / P) rp = np.round(rr, 5) cp = np.round(cc, 5) # pre-allocate arrays for computation texture = np.zeros(P, dtype=np.double) signed_texture = np.zeros(P, dtype=np.int8) output_shape = (image.shape[0], image.shape[1]) output = np.zeros(output_shape, dtype=np.double) rows = image.shape[0] cols = image.shape[1] for r in range(image.shape[0]): for c in range(image.shape[1]): for i in range(P): texture[i] = bilinear_interpolation(image, rows, cols, r + rp[i], c + cp[i], 'C', 0) # signed / thresholded texture for i in range(P): if texture[i] - image[r, c] >= 0: signed_texture[i] = 1 else: signed_texture[i] = 0 # Compute the variance without passing from numpy. # Following the LBP paper, we're taking a biased estimate # of the variance (ddof=0) sum_ = 0.0 var_ = 0.0 for i in range(P): texture_i = texture[i] sum_ += texture_i var_ += texture_i * texture_i var_ = (var_ - (sum_ * sum_) / P) / P if var_ != 0: lbp = var_ else: lbp = np.nan output[r, c] = lbp return np.asarray(output) def bilinear_interpolation(image, rows,cols, r, c, mode, cval): """Bilinear interpolation at a given position in the image. """ minr = int(np.floor(r)) minc = int(np.floor(c)) maxr = int(np.ceil(r)) maxc = int(np.ceil(c)) dr = r - minr dc = c - minc top = (1 - dc) * get_pixel2d(image, rows, cols, minr, minc, mode, cval) \ + dc * get_pixel2d(image, rows, cols, minr, maxc, mode, cval) bottom = (1 - dc) * get_pixel2d(image, rows, cols, maxr, minc, mode, cval) \ + dc * get_pixel2d(image, rows, cols, maxr, maxc, mode, cval) return (1 - dr) * top + dr * bottom def get_pixel2d(image, rows, cols,r, c, mode,cval): """Get a pixel from the image, taking wrapping mode into consideration. """ if (r < 0) or (r >= rows) or (c < 0) or (c >= cols): return cval else: return image[r , c] def circular_LBP(src, n_points, radius): height = src.shape[0] width = src.shape[1] dst = src.copy() src.astype(dtype=np.float32) dst.astype(dtype=np.float32) neighbours = np.zeros((1, n_points), dtype=np.uint8) lbp_value = np.zeros((1, n_points), dtype=np.uint8) for x in range(radius, width - radius - 1): for y in range(radius, height - radius - 1): lbp = 0. # 先计算共n_points个点对应的像素值,使用双线性插值法 for n in range(n_points): theta = float(2 * np.pi * n) / n_points x_n = x + radius * np.cos(theta) y_n = y - radius * np.sin(theta) # 向下取整 x1 = int(math.floor(x_n)) y1 = int(math.floor(y_n)) # 向上取整 x2 = int(math.ceil(x_n)) y2 = int(math.ceil(y_n)) # 将坐标映射到0-1之间 tx = np.abs(x - x1) ty = np.abs(y - y1) # 根据0-1之间的x,y的权重计算公式计算权重 w1 = (1 - tx) * (1 - ty) w2 = tx * (1 - ty) w3 = (1 - tx) * ty w4 = tx * ty # 根据双线性插值公式计算第k个采样点的灰度值 neighbour = src[y1, x1] * w1 + src[y2, x1] * w2 + src[y1, x2] * w3 + src[y2, x2] * w4 neighbours[0, n] = neighbour center = src[y, x] for n in range(n_points): if neighbours[0, n] > center: lbp_value[0, n] = 1 else: lbp_value[0, n] = 0 for n in range(n_points): lbp += lbp_value[0, n] * 2**n # 转换到0-255的灰度空间,比如n_points=16位时结果会超出这个范围,对该结果归一化 dst[y, x] = int(lbp / (2**n_points-1) * 255) return dst if __name__ == "__main__": img = coffee() fig = plt.figure() f1 = fig.add_subplot(121) f1.imshow(img) f1.set_title("image") for colour_channel in (0, 1, 2): img[:, :, colour_channel] = local_binary_pattern( img[:, :, colour_channel], 8,1.0) print img[:, :, colour_channel] print circular_LBP(img[:, :, colour_channel], 8,1) f2 = fig.add_subplot(122) f2.imshow(img) f2.set_title("LBP") plt.show() """ [[ 12 10 12 ..., 198 227 46] [ 11 0 0 ..., 7 3 5] [ 12 0 0 ..., 5 2 14] ..., [ 13 105 23 ..., 19 6 203] [222 23 7 ..., 7 14 165] [ 84 26 15 ..., 174 185 179]] [[ 12 10 12 ..., 198 227 46] [ 11 54 7 ..., 6 3 5] [ 12 112 98 ..., 100 2 14] ..., [ 13 36 20 ..., 0 6 203] [222 23 7 ..., 7 14 165] [ 84 26 15 ..., 174 185 179]] """
相关的双线性插值
双线性插值,这个名字咋一听很高大上的样纸,再在维基百科上一查(见文末,我去,一堆的公式吓死人),像俺这种半文盲,看到公式脑子就懵的类型,真心给跪。虽然看着好复杂,但仔细一看道理再简单不过了,所以还是自己梳理一下好。
双线性插值,顾名思义就是两个方向的线性插值加起来(这解释过于简单粗暴,哈哈)。所以只要了解什么是线性插值,分别在x轴和y轴都做一遍,就是双线性插值了。
线性插值的概念也非常简单粗暴,就是两个点A,B,要在AB中间插入一个点C(点C坐标在AB连线上),就直接让C的值落在AB的值的连线上就可以了。
如A点坐标(0,0),值为3,B点坐标(0,2),值为5,那要对坐标为(0,1)的点C进行插值,就让C落在AB线上,值为4就可以了。
但是如果C不在AB的线上肿么办捏,所以就有了双线性插值。如图,已知Q12,Q22,Q11,Q21,但是要插值的点为P点,这就要用双线性插值了,首先在x轴方向上,对R1和R2两个点进行插值,这个很简单,然后根据R1和R2对P点进行插值,这就是所谓的双线性插值。
附:维基百科--双线性插值:
双线性插值,又称为双线性内插。在数学上,双线性插值是有两个变量的插值函数的线性插值扩展,其核心思想是在两个方向分别进行一次线性插值。
假如我们想得到未知函数
在点
的值,假设我们已知函数
在
,
,
, 及
四个点的值。
首先在 x 方向进行线性插值,得到
然后在 y 方向进行线性插值,得到
这样就得到所要的结果
,
如果选择一个坐标系统使得
的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1),那么插值公式就可以化简为
或者用矩阵运算表示为
与这种插值方法名称不同的是,这种插值方法的结果通常不是线性的,它的形式是
常数的数目都对应于给定的 f 的数据点数目
线性插值的结果与插值的顺序无关。首先进行 y 方向的插值,然后进行 x 方向的插值,所得到的结果是一样的。



 在点
在点 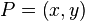 的值,假设我们已知函数
的值,假设我们已知函数  ,
,  ,
,  , 及
, 及  四个点的值。
四个点的值。
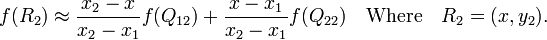
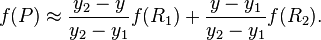
 ,
,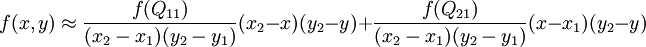

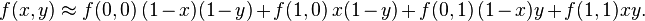






 浙公网安备 33010602011771号
浙公网安备 33010602011771号