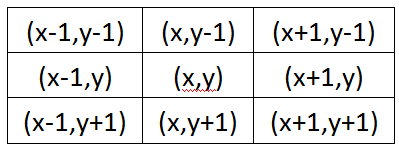图像处理1 高斯模糊

 

简介

高斯模糊（英语：Gaussian Blur），也叫高斯平滑，是在Adobe Photoshop、GIMP以及Paint.NET等图像处理软件中广泛使用的处理效果，通常用它来减少图像噪声以及降低细节层次。这种模糊技术生成的图像，其视觉效果就像是经过一个半透明屏幕在观察图像，这与镜头焦外成像效果散景以及普通照明阴影中的效果都明显不同。高斯平滑也用于计算机视觉算法中的预先处理阶段，以增强图像在不同比例大小下的图像效果（参见尺度空间表示以及尺度空间实现）。 从数学的角度来看，图像的高斯模糊过程就是图像与正态分布做卷积。由于正态分布又叫作高斯分布，所以这项技术就叫作高斯模糊。图像与圆形方框模糊做卷积将会生成更加精确的焦外成像效果。

由于高斯函数的傅立叶变换是另外一个高斯函数，所以高斯模糊对于图像来说就是一个低通滤波器，也就是说，低波通过，高波滤去。对于图像来讲，就是在低频的部分通过，对于高频的地方滤去。对图像的边缘等细节部分进行模糊，这是由高斯模糊的公式的性质决定的。这点，经常在数字图像处理中利用，以在图像仿真图像重打样等领域进行利用。

公式如下。

 

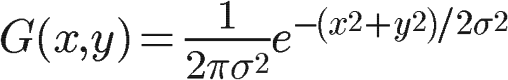
σ是标准差，在这里又叫做高斯半径。σ2表示的意思就是方差。f(x)是概率，μ是均值，即期望。即这个公式表示的意思在μ附近的概率。离μ越近，即σ越小，其概率越大；离μ越远，即σ越大，其概率越小。σ的取值范围是[0.1~250]。

 

高斯掩膜

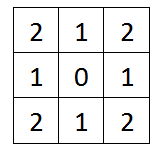
转自链接，对于图像中任意一点(x,y)，它周围的坐标为：

中间的(x,y)就是我们公式中的了， 当遍历(x-1,y-1)...(x+1,y+1)时,

：

(只剩下常数没有x,y是因为在相减的过程中把x，y抵消掉了)

：

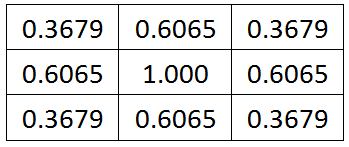
(这里取sigma为1.0)

归一化就得到高！斯！掩！膜！了：

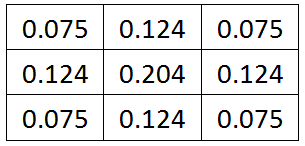
所以你看，高斯掩膜的求解与位置(x,y)无关，因为在计算过程中x,y被抵消掉了，

因！此！——

高斯掩膜只要求解一次就够了！ 当得到了这个模板，对图像的所有像素用这同一套模板去卷积就OK了！

实现

由上可知，高斯掩膜翻转不变，滤波函数功能与卷积一致。

运行结果如下。

 

# coding:utf8
import cv2
from filter import *
from  scipy.signal.signaltools import convolve2d


class MyGaussianBlur():
    # 初始化
    def __init__(self, kernel=3, sigema=1.5):
        self.kernel = kernel if kernel>=3 else 3
        self.radius = (kernel-1)/2
        self.sigema = sigema

    # 高斯的计算公式
    def calc(self, x, y):
        res1 = 1 / (2 * math.pi * self.sigema * self.sigema)
        res2 = math.exp(-(x * x + y * y) / (2 * self.sigema * self.sigema))
        return res1 * res2

    # 得到滤波模版
    def template(self):
        sideLength = self.kernel
        result = np.zeros((sideLength, sideLength))
        for i in range(sideLength):
            for j in range(sideLength):
                result[i, j] = self.calc(i - self.radius, j - self.radius)
        all = result.sum()
        return result / all

    # 卷积滤波函数
    def filter_conv(self, image):
        template = self.template()
        arr = np.array(image)
        channel = arr.shape[2]
        newData = arr.copy()
        for k in range(channel):
            newData[:, :, k] = convolve2d(arr[:, :, k], template, mode='same')
        return newData

    # 滤波函数
    def filter(self, image):
        template = self.template()
        arr = np.array(image)
        height = arr.shape[0]
        width = arr.shape[1]
        channel = arr.shape[2]
        newData = arr.copy()
        for k in range(channel):
            for i in range(self.radius, height - self.radius):
                for j in range(self.radius, width - self.radius):
                    t = arr[i - self.radius:i + self.radius + 1, j - self.radius:j + self.radius + 1, k]
                    a = np.multiply(t, template)
                    newData[i, j, k] = int(a.sum())
        return newData




if __name__ == '__main__':
    img = cv2.imread('test_data/0010.jpg')
    sigma=1.0
    kernel=3
    cv2.imshow('img0', img)

    img1 = cv2.GaussianBlur(img, (kernel, kernel), sigma)
    cv2.imshow('img1', img1)

    img2 = MyGaussianBlur(kernel=kernel, sigema=sigma).filter(img)
    cv2.imshow('img2', img2)

    img3 = MyGaussianBlur(kernel=kernel, sigema=sigma).filter_conv(img)
    cv2.imshow('img3', img3)
    cv2.waitKey(0)

    print MyGaussianBlur(kernel=kernel, sigema=sigma).template()
    """
    [[ 0.07511361  0.1238414   0.07511361]
     [ 0.1238414   0.20417996  0.1238414 ]
     [ 0.07511361  0.1238414   0.07511361]]
    """