BP神经网络

代码为MNIST数据集上运行简单BP神经网络的python实现。

 

 以下公式和文字来自Wanna_Go的博文 http://www.cnblogs.com/wxshi/p/6077734.html，包含详尽的描述和推导。

BP神经网络

单个神经元

　　神经网络是由多个“神经元”组成，单个神经元如下图所示：

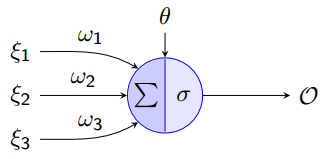
　　这其实就是一个单层感知机，输入是由ξ1 ,ξ2 ,ξ3和Θ组成的向量。其中Θ为偏置(bias),σ为激活函数(transfer function)，本文采用的是sigmoid函数，功能与阶梯函数(step function)相似控制设神经元的输出，它的优点是连续可导。

是神经元的输出，结果为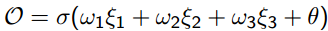

可以看得出这个“神经元”的输入-输出映射其实就是一个逻辑回归，常用的激活函数还有双曲正切函数 。

 激活函数

sigmoid：函数

取值范围为[0,1],它的图像如下：

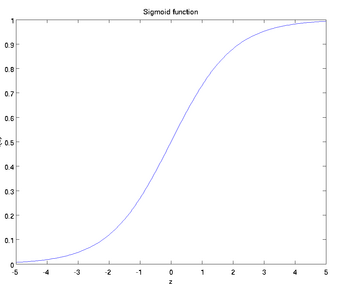
求导结果为：

 

tanh函数：

 

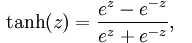
取值范围为[-1,1],图像如下：

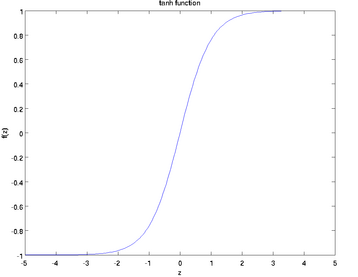
 求导数结果为。本文采用的是sigmoid函数作为激活函数。

神经网络模型

神经网络将许多“神经元”联结在一起，一个神经元的输出可以是另一个“神经元”的输入，神经元之间的传递需要乘法上两个神经元对应的权重，下图就是一个简单的神经网络：

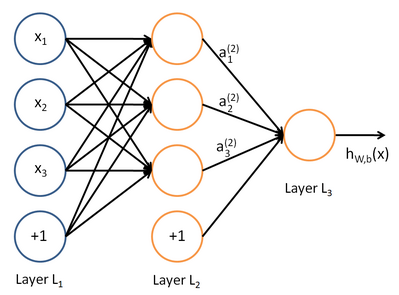
这是一个三层的神经网络，使用圆圈来表示神经元的输入，“+1”被称为偏置节点，从左到右依次为输入层、隐藏层和输出层，从图中可以看出，有3个输入节点、3个隐藏节点和一个输出单元(偏置不接受输入)。

本例神经网络的参数有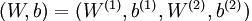，其中 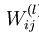是第l层第 j 单元与 l+1层第  \textstyle i 单元之间的联接参数，即：节点连线的权重，本图中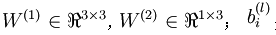 是第l+1 层第i单元的偏置项。

向前传播

　　机器学习(有监督)的任务无非是损失函数最小化，BP神经网络的原理是前向传播得到目标值（分类），再通过后向传播对data loss进行优化求出参数。可见最优化部分

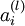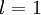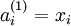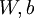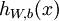 　　\textstyle a^{(l)}_i 表示\textstyle l 层第 \textstyle i 单元激活值（输出值）。当 \textstyle l=1 时， \textstyle a^{(1)}_i = x_i ，也就是第 \textstyle i 个输入值。对于给定参数集 \textstyle W,b ，\textstyle h_{W,b}(x) 来表示神经网络最后计算输出的结果。上图神经网络计算步骤如下：


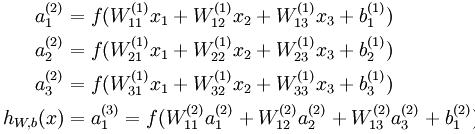
 可以看出，神经网络的核心思想是这一层的输出乘上相应的权重加上偏置，带入激活函数后的输出又是下一层的输入。用 \textstyle z^{(l)}_i 表示第\textstyle l层第\textstyle i 单元输入加权和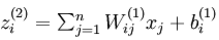 ，则 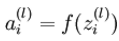。使用向量化表示方法表示，上面的公式可以简写为：

 

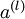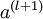这些计算步骤就是前向传播，将计算过程进行推广，给定第 \textstyle l 层的激活值 \textstyle a^{(l)}，第 \textstyle l+1层的激活值\textstyle a^{(l+1)}的计算过程为：

 

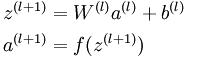
反向传播

在前向传播中，我们得到了神经网络的预测值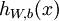\textstyle h_{W,b}(x)，这时候可以通过反向传播的方法计算出参数

符号定义

神经网络21.png：第l层第j个节点的输入。

神经网络22.png：从第l-1层第i个节点到第l层第j个节点的权值。

神经网络23.png：Sigmoid激活函数。

神经网络24.png：：第l层第j个节点的偏置。

神经网络25.png：：第l层第j个节点的输出。

神经网络26.png：：输出层第j个节点的目标值(label)。

使用梯度下降的方法求解参数，在求解的过程中需要对输出层和隐藏层分开计算

输出层权重计算

　　给定样本标签神经网络28.png和模型输出结果神经网络29.png，输出层的损失函数为：

神经网络27.png

这其实就是均方差项，训练的目标是最小化该误差，使用梯度下降方法进行优化，对上式子对权重W进行求导：

神经网络31.png

，整理神经网络32.png，

其中神经网络37.png=神经网络36.png带入神经网络34.png，对sigmoid求导得：

神经网络35.png

输出层第k个节点的输入神经网络38.png等于上一层第j个节点的输出神经网络39.png乘上神经网络100.png，即神经网络38.png=神经网络39.png神经网络100.png，而上一层的输出神经网络39.png与输出层的权重变量神经网络100.png无关，可以看做一个常数，所以直接求导可以得到：

 

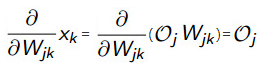
所以将神经网络36.png=神经网络37.png带入式子中就得到：

神经网络43.png

为了方便表示将上式子记作：

神经网络44.png

其中：

 隐藏层权重计算

采用同样方法对隐藏层的权重进行计算，与前面不同的是关于隐藏层和前一层权重的调整

神经网络46.png

整理

神经网络47.png

替换sigmoid函数

神经网络48.png

对sigmoid求导

神经网络49.png

把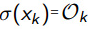带入进去，使用求导的链式法则：

神经网络51.png

输出层的输入等于上一层的输入乘以相应的权重，即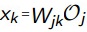：于是得到

神经网络54.png

对进行求导（神经网络37.png=神经网络36.png，同样适用于j），

神经网络56.png

同输出层计算的方法一样，再次利用，j换成i，k换成j同样成立，带入进去:

神经网络57.png

整理，得到：

神经网络59.png

其中：神经网络45.png

 

 我们还可以仿照神经网络58.png的定义来定义一个神经网络60.png，得到：

神经网络61.png

其中：神经网络70.png

 偏置调整

　　从上面的计算步骤中可以看出：例如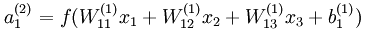，偏置节点是不存在对应的权值参数，也就是不存在关于权值变量的偏导数。

对偏置直接求导：

神经网络68.png

又有

神经网络63.png

 

 得到：

神经网络65.png，其中：神经网络45.png

BP算法步骤

1. 随机初始化W和b，需要注意的是，随机初始化并是不是全部置为0，如果所有参数都是用相同的值初始化，那么所有隐藏单元最终会得到与输入值相关、相同的函数(也就是说，对于所有 \textstyle i，\textstyle W^{(1)}_{ij}都会取相同的值，那么对于任何输入 \textstyle x 都会有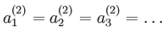： )，随机初始化的目的是使对称失效。

2.对每个输出节点按照这个公式计算delta：

神经网络71.png

3.对每个隐藏节点按照这个公式计算delta：

神经网络72.png

4.更新W和b的公式为：

神经网络73.png

 

并更新参数神经网络74.png，这里的η是学习率。

 

 1 # coding:utf8
 2 import cPickle
 3 import numpy as np
 4 
 5 
 6 class Network(object):
 7     def __init__(self, sizes):
 8         self.num_layers = len(sizes)
 9         self.sizes = sizes
10         self.biases = [np.random.randn(y, 1) for y in sizes[1:]]  # L(n-1)->L(n)
11         self.weights = [np.random.randn(y, x)
12                         for x, y in zip(sizes[:-1], sizes[1:])]
13 
14     def feedforward(self, a):
15         for b_, w_ in zip(self.biases, self.weights):
16             a = self.sigmoid(np.dot(w_, a)+b_)
17         return a
18 
19     def SGD(self, training_data, test_data,epochs, mini_batch_size, eta):
20         n_test = len(test_data)
21         n = len(training_data)
22         for j in xrange(epochs):
23             np.random.shuffle(training_data)  # shuffle
24             for k in xrange(0, n, mini_batch_size):
25                 mini_batch = training_data[k:k+mini_batch_size]
26                 self.update_mini_batch(mini_batch, eta)
27             print "Epoch {0}: {1} / {2}".format(
28                     j, self.evaluate(test_data), n_test)
29 
30     def update_mini_batch(self, mini_batch, eta):
31         for x, y in mini_batch:
32             delta_b, delta_w = self.backprop(x, y)
33             self.weights -= eta/len(mini_batch)*delta_w
34             self.biases -= eta/len(mini_batch)*delta_b
35 
36     def backprop(self, x, y):
37         b=np.zeros_like(self.biases)
38         w=np.zeros_like(self.weights)
39         a_ = x
40         a = [x]
41         for b_, w_ in zip(self.biases, self.weights):
42             a_ = self.sigmoid(np.dot(w_, a_)+b_)
43             a.append(a_)
44         for l in xrange(1, self.num_layers):
45             if l==1:
46                 delta= self.sigmoid_prime(a[-1])*(a[-1]-y)  # O(k)=a[-1], t(k)=y
47             else:
48                 sp = self.sigmoid_prime(a[-l])   # O(j)=a[-l]
49                 delta = np.dot(self.weights[-l+1].T, delta) * sp
50             b[-l] = delta
51             w[-l] = np.dot(delta, a[-l-1].T)
52         return (b, w)
53 
54     def evaluate(self, test_data):
55         test_results = [(np.argmax(self.feedforward(x)), y)
56                         for (x, y) in test_data]
57         return sum(int(x == y) for (x, y) in test_results)
58 
59     def sigmoid(self,z):
60         return 1.0/(1.0+np.exp(-z))
61 
62     def sigmoid_prime(self,z):
63         return z*(1-z)
64 
65 if __name__ == '__main__':
66 
67         def get_label(i):
68             c=np.zeros((10,1))
69             c[i]=1
70             return c
71 
72         def get_data(data):
73             return [np.reshape(x, (784,1)) for x in data[0]]
74 
75         f = open('mnist.pkl', 'rb')
76         training_data, validation_data, test_data = cPickle.load(f)
77         training_inputs = get_data(training_data)
78         training_label=[get_label(y_) for y_ in training_data[1]]
79         data = zip(training_inputs,training_label)
80         test_inputs = training_inputs = get_data(test_data)
81         test = zip(test_inputs,test_data[1])
82         net = Network([784, 30, 10])
83         net.SGD(data,test,20,10, 3.0,)  # 9496/10000

 

posted on 2016-11-25 21:49  1357  阅读(1990)  评论(0)  编辑  收藏  举报

导航