李超线段树学习笔记
一、算法介绍
李超线段树是一种用于维护平面直角坐标系内线段关系的数据结构。它常被用来处理这样一种形式的问题：给定一个平面直角坐标系，支持动态插入一条线段，询问从某一个位置$ (x,+\infty) $向下看能看到的最高的一条线段。
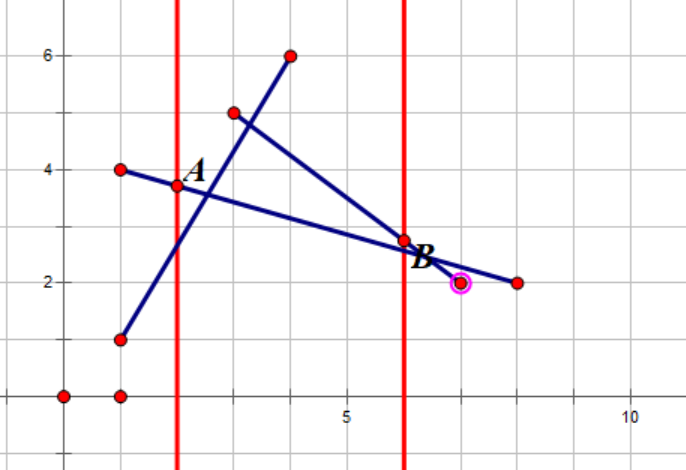如图，有三条线段，两条红色竖线代表两个询问，则点$ A $与点$ B $就是询问到的答案
李超线段树的核心是维护每个区间的“最优势线段”，即在每个区间的中点处最高的线段。询问时我们可以对所有包含横坐标为$ x $的位置的区间上的最优势线段计算答案，最后取个$ max $。其实就相当于一个记录当前区间最高线段的，不下传标记的线段树。
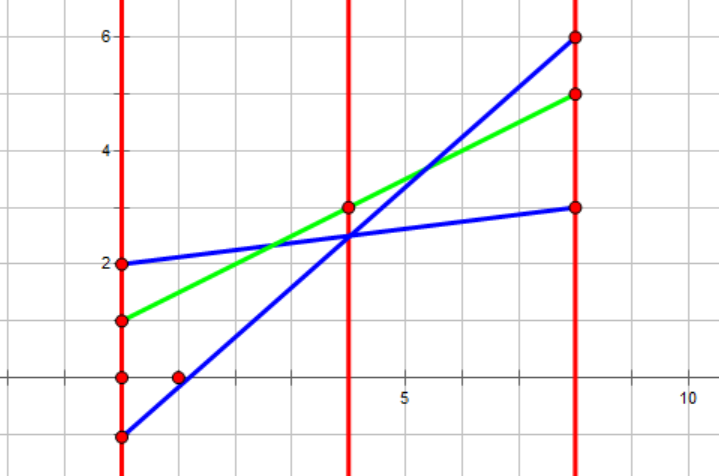
如图，对于区间$ [0,8] $，绿色线段是“最优势线段”
对于修改，我们先把线段的值域分割到线段树的区间上，每次访问一个完整的包含在线段值域中的区间时：
1、若当前区间还没有记录最优势线段，则记录最优势线段并返回。
2、若当前区间的最优势线段被插入的线段完全覆盖，则把最优势线段修改为被插入线段并返回。
3、若当前区间的最优势线段把被插入线断完全覆盖，则直接返回。
4、若当前区间最优势线段与被插入线段有交，则先判断哪条线段在当前区间更优，并把更劣的线段下传到交点所在子区间。（交点两边的部分被这两条线段分别控制，而我们已经让在中点更优的那条线段作为区间最优势线段，因此更劣的那条线段只有可能在交点所在子区间超过当前区间的最优势线段）
复杂度分析：
修改部分：我们每次把一条线段的值域分隔到$ O(\log n) $个区间，每个区间最多把标记下传$ O(\log n) $层，因此修改的时间复杂度为$ O(\log^2 n) $。（但实测常数很小）
查询部分：每次在线段树上从上到下扫一遍，时间复杂度为$ O(\log n) $
二、例题
1、bzoj1568 [JSOI2008]Blue Mary开公司
是道裸题。
代码：
#include<cstdio> #include<cstring> #include<cmath> #include<cstdlib> #include<algorithm> #include<vector> #define ll long long #define mod 1000000007 #define eps 1e-12 #define maxn 50010 inline ll read() { ll x=0; char c=getchar(),f=1; for(;c<'0'||'9'<c;c=getchar())if(c=='-')f=-1; for(;'0'<=c&&c<='9';c=getchar())x=x*10+c-'0'; return x*f; } inline void write(ll x) { static int buf[20],len; len=0; if(x<0)x=-x,putchar('-'); for(;x;x/=10)buf[len++]=x%10; if(!len)putchar('0'); else while(len)putchar(buf[--len]+'0'); } inline void writeln(ll x){write(x); putchar('\n');} inline void writesp(ll x){write(x); putchar(' ');} struct line{ double k,b; int l,r; }sgt[4*maxn]; int n; char op[10]; inline double calc(line a,int pos){return a.k*pos+a.b;} inline int cross(line a,line b){return floor((a.b-b.b)/(b.k-a.k));} void build(int now,int l,int r) { sgt[now].k=sgt[now].b=0; sgt[now].l=1; sgt[now].r=50000; if(l==r)return; int mid=(l+r)>>1; build(now<<1,l,mid); build(now<<1|1,mid+1,r); } void modify(int now,int l,int r,line k) { if(k.l<=l&&r<=k.r){ if(calc(k,l)-calc(sgt[now],l)>eps&&calc(k,r)-calc(sgt[now],r)>eps)sgt[now]=k; else if(calc(k,l)-calc(sgt[now],l)>eps||calc(k,r)-calc(sgt[now],r)>eps){ int mid=(l+r)>>1; if(calc(k,mid)-calc(sgt[now],mid)>eps){ line tmp=k; k=sgt[now]; sgt[now]=tmp; } if(cross(k,sgt[now])-mid<-eps)modify(now<<1,l,mid,k); else modify(now<<1|1,mid+1,r,k); } } else{ int mid=(l+r)>>1; if(k.l<=mid)modify(now<<1,l,mid,k); if(mid<k.r)modify(now<<1|1,mid+1,r,k); } } double query(int now,int l,int r,int x) { if(l==r)return calc(sgt[now],x); else{ int mid=(l+r)>>1; double ans=calc(sgt[now],x); if(x<=mid)return std::max(ans,query(now<<1,l,mid,x)); else return std::max(ans,query(now<<1|1,mid+1,r,x)); } } int main() { // freopen("bzoj1568.in","r",stdin); // freopen("bzoj1568.out","w",stdout); n=read(); build(1,1,50000); for(int i=1;i<=n;i++){ scanf("%s",op); if(op[0]=='P'){ double s,p; scanf("%lf%lf",&s,&p); line now; now.l=1; now.r=50000; now.k=p; now.b=s-p; modify(1,1,50000,now); } else{ int x=read(); writeln(floor(query(1,1,50000,x)/100)); } } // fclose(stdin); fclose(stdout); return 0; }
容易发现，每个机器人的位置是一个关于时间的一次分段函数，因此可以把询问离线下来，先用李超线段树维护对于每个时间点，位置-时间函数的最大值和最小值（正半轴和负半轴），然后就可以直接回答询问。因为横坐标较大，所以我们需要对线段树区间坐标进行离散化。
代码：
#include<cstdio> #include<cstring> #include<cmath> #include<cstdlib> #include<algorithm> #include<vector> #define ll long long #define mod 1000000007 #define Mod1(x) (x>=mod?x-mod:x) #define Mod2(x) (x<0?x+mod:x) #define maxn 600010 inline ll read() { ll x=0; char c=getchar(),f=1; for(;c<'0'||'9'<c;c=getchar())if(c=='-')f=-1; for(;'0'<=c&&c<='9';c=getchar())x=x*10+c-'0'; return x*f; } inline void write(ll x) { static int buf[20],len; len=0; if(x<0)x=-x,putchar('-'); for(;x;x/=10)buf[len++]=x%10; if(!len)putchar('0'); else while(len)putchar(buf[--len]+'0'); } inline void writeln(ll x){write(x); putchar('\n');} inline void writesp(ll x){write(x); putchar(' ');} struct line{ int l,r; ll k,b; }; struct point{ line mx,mn; int flag; }sgt[4*maxn]; struct opt{ int rk,k,v; }md[maxn]; ll pos[maxn]; int last[maxn],Time[maxn],q[maxn]; int n,m; char op[10]; ll calc(line a,int x){return a.k*x+a.b;} long double cross(line a,line b){return (long double)(a.b-b.b)/(b.k-a.k);} void modify(int now,int l,int r,line k) { // printf("%d %d %d %d %d %lld %lld\n",now,l,r,Time[k.l],Time[k.r],k.k,k.b); // system("pause"); if(k.l<=l&&r<=k.r){ if(!sgt[now].flag){ sgt[now].flag=1; sgt[now].mx=sgt[now].mn=k; return; } line tmp=k; if(calc(tmp,Time[l])>calc(sgt[now].mx,Time[l])&&calc(tmp,Time[r])>calc(sgt[now].mx,Time[r]))sgt[now].mx=tmp; else if(calc(tmp,Time[l])>calc(sgt[now].mx,Time[l])||calc(tmp,Time[r])>calc(sgt[now].mx,Time[r])){ int mid=(l+r)>>1; if(calc(tmp,Time[mid])>calc(sgt[now].mx,Time[mid])){ line t=tmp; tmp=sgt[now].mx; sgt[now].mx=t; } // puts("max ->"); if(cross(sgt[now].mx,tmp)<=Time[mid])modify(now<<1,l,mid,tmp); else modify(now<<1|1,mid+1,r,tmp); } tmp=k; if(calc(tmp,Time[l])<calc(sgt[now].mn,Time[l])&&calc(tmp,Time[r])<calc(sgt[now].mn,Time[r]))sgt[now].mn=tmp; else if(calc(tmp,Time[l])<calc(sgt[now].mn,Time[l])||calc(tmp,Time[r])<calc(sgt[now].mn,Time[r])){ int mid=(l+r)>>1; if(calc(tmp,Time[mid])<calc(sgt[now].mn,Time[mid])){ line t=tmp; tmp=sgt[now].mn; sgt[now].mn=t; } // puts("min ->"); if(cross(sgt[now].mn,tmp)<=Time[mid])modify(now<<1,l,mid,tmp); else modify(now<<1|1,mid+1,r,tmp); } } else{ int mid=(l+r)>>1; if(k.l<=mid)modify(now<<1,l,mid,k); if(mid<k.r)modify(now<<1|1,mid+1,r,k); } } ll query(int now,int l,int r,int x) { // printf("%d %d %d %d : %d %d %lld %lld || %d %d %lld %lld\n",now,l,r,x,sgt[now].mx.l,sgt[now].mx.r,sgt[now].mx.k,sgt[now].mx.b,sgt[now].mn.l,sgt[now].mn.r,sgt[now].mn.k,sgt[now].mn.b); if(l==r)return std::max(calc(sgt[now].mx,Time[x]),-calc(sgt[now].mn,Time[x])); else{ int mid=(l+r)>>1; ll ans=std::max(calc(sgt[now].mx,Time[x]),-calc(sgt[now].mn,Time[x])); if(x<=mid)return std::max(ans,query(now<<1,l,mid,x)); else return std::max(ans,query(now<<1|1,mid+1,r,x)); } } int main() { // writeln(sizeof(sgt)); n=read(); m=read(); for(int i=1;i<=n;i++) pos[i]=read(); int cnt1=0,cnt2=0; for(int i=1;i<=m;i++){ Time[i]=read(); last[i]=(Time[i]==Time[i-1]?last[i-1]:i); scanf("%s",op); if(op[0]=='c'){ int k=read(),v=read(); md[++cnt1]={last[i],k,v}; } else q[++cnt2]=last[i]; } memset(last,0,sizeof(last)); for(int i=1;i<=cnt1;i++){ pos[md[i].k]+=(ll)md[last[md[i].k]].v*(Time[md[i].rk]-Time[md[last[md[i].k]].rk]); line init={md[last[md[i].k]].rk,md[i].rk,md[last[md[i].k]].v,pos[md[i].k]-(ll)md[last[md[i].k]].v*Time[md[i].rk]}; modify(1,0,m,init); // puts("cxktxdy"); last[md[i].k]=i; } for(int i=1;i<=n;i++){ pos[i]+=(ll)md[last[i]].v*(Time[m]-Time[md[last[i]].rk]); line init={md[last[i]].rk,m,md[last[i]].v,pos[i]-(ll)md[last[i]].v*Time[m]}; modify(1,0,m,init); // puts("lgtxdy"); } for(int i=1;i<=cnt2;i++) writeln(query(1,0,m,q[i])); return 0; }
首先直接上链剖，然后就变成了一道裸题。但是查询似乎不太一样，是查询区间的最小值。但是我们可以发现，一次函数是单调的，因此我们可以很方便的查询一次函数在某个区间内的最值。因此直接在插入线段的时候顺便维护一下区间最值就可以回答询问了。不过这个复杂度。。。链剖一个$ \log $，李超线段树两个$ \log $，总时间复杂度是$ O(m \log^3 n) $。。。不过李超线段树常数很小，所以还是可以过的。
代码：
#include<cstdio> #include<cstring> #include<cmath> #include<cstdlib> #include<algorithm> #include<vector> #define ll long long #define inf 123456789123456789ll #define mod 1000000007 #define Mod1(x) (x>=mod?x-mod:x) #define Mod2(x) (x<0?x+mod:x) #define maxn 100010 inline ll read() { ll x=0; char c=getchar(),f=1; for(;c<'0'||'9'<c;c=getchar())if(c=='-')f=-1; for(;'0'<=c&&c<='9';c=getchar())x=x*10+c-'0'; return x*f; } inline void write(ll x) { static int buf[20],len; len=0; if(x<0)x=-x,putchar('-'); for(;x;x/=10)buf[len++]=x%10; if(!len)putchar('0'); else while(len)putchar(buf[--len]+'0'); } inline void writeln(ll x){write(x); putchar('\n');} inline void writesp(ll x){write(x); putchar(' ');} struct line{ ll l,r,k,b; friend inline ll calc(line a,ll b){return a.k*b+a.b;} friend inline ll calc_min(line a,ll l,ll r){return (a.k>0?calc(a,l):calc(a,r));} friend inline double cross(line a,line b){return (double)(a.b-b.b)/(b.k-a.k);} }; struct point{ line l; ll mn; }sgt[4*maxn]; struct edge{ int to,nxt,d; }e[2*maxn]; int fir[maxn],fa[maxn],dep[maxn],size[maxn],hson[maxn],id[maxn],top[maxn]; ll dist[maxn],val[maxn]; int seq[maxn]; int n,m,tot; inline void add_edge(int x,int y,int d){e[tot].to=y; e[tot].d=d; e[tot].nxt=fir[x]; fir[x]=tot++;} void dfs1(int now) { size[now]=1; hson[now]=0; for(int i=fir[now];~i;i=e[i].nxt) if(e[i].to!=fa[now]){ fa[e[i].to]=now; dep[e[i].to]=dep[now]+1; dist[e[i].to]=dist[now]+e[i].d; dfs1(e[i].to); size[now]+=size[e[i].to]; if(size[e[i].to]>size[hson[now]])hson[now]=e[i].to; } } void dfs2(int now,int tp) { id[now]=++tot; seq[tot]=now; top[now]=tp; if(hson[now])dfs2(hson[now],tp); for(int i=fir[now];~i;i=e[i].nxt) if(e[i].to!=fa[now]&&e[i].to!=hson[now])dfs2(e[i].to,e[i].to); } void build(int now,int l,int r) { sgt[now].l={l,r,0,inf}; sgt[now].mn=inf; if(l<r){ int mid=(l+r)>>1; build(now<<1,l,mid); build(now<<1|1,mid+1,r); } } void add(int now,int l,int r,line k) { // printf("%d %d %d %lld %lld %lld %lld\n",now,l,r,val[k.l],val[k.r],k.k,k.b); if(k.l<=l&&r<=k.r){ if(calc(k,val[l])<calc(sgt[now].l,val[l])&&calc(k,val[r])<calc(sgt[now].l,val[r])){ sgt[now].l=k; sgt[now].mn=calc_min(k,val[l],val[r]); if(l<r)sgt[now].mn=std::min(sgt[now].mn,std::min(sgt[now<<1].mn,sgt[now<<1|1].mn)); } else if(calc(k,val[l])<calc(sgt[now].l,val[l])||calc(k,val[r])<calc(sgt[now].l,val[r])){ int mid=(l+r)>>1; if(calc(k,val[mid])<calc(sgt[now].l,val[mid])){ line tmp=k; k=sgt[now].l; sgt[now].l=tmp; } if(cross(k,sgt[now].l)<=val[mid])add(now<<1,l,mid,k); else add(now<<1|1,mid+1,r,k); sgt[now].mn=std::min(std::min(sgt[now<<1].mn,sgt[now<<1|1].mn),calc_min(sgt[now].l,val[l],val[r])); } } else{ int mid=(l+r)>>1; if(k.l<=mid)add(now<<1,l,mid,k); if(mid<k.r)add(now<<1|1,mid+1,r,k); sgt[now].mn=std::min(std::min(sgt[now<<1].mn,sgt[now<<1|1].mn),calc_min(sgt[now].l,val[l],val[r])); } // printf("%d %d %d %lld ^^^^^^^^^^^^^^^\n",now,l,r,sgt[now].mn); } ll getmin(int now,int l,int r,int x,int y) { // printf("%d %d %d %d %d ****\n",now,l,r,x,y); if(x<=l&&r<=y)return sgt[now].mn; else{ int mid=(l+r)>>1; ll ans=calc_min(sgt[now].l,val[std::max(x,l)],val[std::min(y,r)]); if(x<=mid)ans=std::min(ans,getmin(now<<1,l,mid,x,y)); if(mid<y)ans=std::min(ans,getmin(now<<1|1,mid+1,r,x,y)); return ans; } } int getlca(int x,int y) { while(top[x]!=top[y]){ if(dep[top[x]]<dep[top[y]]){ int tmp=x; x=y; y=tmp; } x=fa[top[x]]; } return (dep[x]<dep[y]?x:y); } void modify(int u,int v,ll a,ll b) { int x=u,y=v,lca=getlca(x,y); ll d=dist[x]+dist[y]-2*dist[lca]; while(dep[top[x]]>dep[lca]){ // printf("&&&& %d %d\n",top[x],x); line tmp={id[top[x]],id[x],-a,a*(dist[u]-dist[x])+b+val[id[x]]*a}; add(1,1,n,tmp); x=fa[top[x]]; } while(dep[top[y]]>dep[lca]){ // printf("&&&& %d %d\n",top[y],y); line tmp={id[top[y]],id[y],a,a*(d-dist[v]+dist[y])+b-val[id[y]]*a}; add(1,1,n,tmp); y=fa[top[y]]; } if(x==lca){ // printf("**** %d %d\n",x,y); line tmp={id[x],id[y],a,a*(dist[u]-dist[x])+b-val[id[x]]*a}; add(1,1,n,tmp); } else{ // puts("qaq"); // printf("**** %d %d\n",y,x); line tmp={id[y],id[x],-a,a*(dist[u]-dist[y])+b+val[id[y]]*a}; add(1,1,n,tmp); } } ll query(int u,int v) { ll ans=inf; while(top[u]!=top[v]){ if(dep[top[u]]<dep[top[v]]){ int tmp=u; u=v; v=tmp; } // printf("%d %d %lld\n",top[u],u,ans); ans=std::min(ans,getmin(1,1,n,id[top[u]],id[u])); u=fa[top[u]]; } // printf("%d %d %lld\n",u,v,ans); if(dep[u]<dep[v])ans=std::min(ans,getmin(1,1,n,id[u],id[v])); else ans=std::min(ans,getmin(1,1,n,id[v],id[u])); return ans; } int main() { n=read(); m=read(); memset(fir,255,sizeof(fir)); tot=0; for(int i=1;i<n;i++){ int x=read(),y=read(),z=read(); add_edge(x,y,z); add_edge(y,x,z); } fa[1]=-1; dep[1]=dist[1]=0; dfs1(1); tot=0; dfs2(1,1); // for(int i=1;i<=n;i++) // writesp(i),writesp(fa[i]),writesp(dep[i]),writesp(dist[i]), // writesp(size[i]),writesp(hson[i]),writesp(id[i]),writeln(top[i]); for(int i=1;i<=n;i++) if(top[seq[i]]==seq[i])val[i]=val[i-1]+1; else val[i]=val[i-1]+(dist[seq[i]]-dist[seq[i-1]]); // for(int i=1;i<=n;i++) // printf("%d %lld\n",i,val[i]); build(1,1,n); for(int i=1;i<=m;i++){ int op=read(); if(op==1){ int u=read(),v=read(),a=read(),b=read(); modify(u,v,a,b); } else{ int u=read(),v=read(); writeln(query(u,v)); } } return 0; }
