计算机科学导论笔记-数字系统
数字系统是用不同符号表示数字的系统,具体分为位置系统和非位置系统
- 位置化系统
符号占据的位置决定了其表示的值,在系统中是这样表示:
- 十进制系统
十进制中b为10,并且使用0-9这个字符集来表示。- 整数:使用位置化表示后如下图

-
实数:使用二进制后如下图
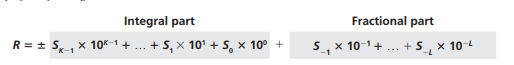
- 整数:使用位置化表示后如下图
-
二进制系统
二进制中b为2字符集仅有0和1,在计算机中程序和数据都由0和1组成(书中用的是位串,即string of bits ),这是由于计算机硬件最基础的原理就是电子的开关,不同的开关代表不同的状。- 整数
我们可以把整数表示为b为2的位串
- 实数
可以将实数分为两个部分,整数部分和小数部分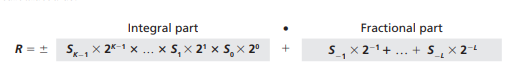
注意的是后面小数的表达方法实际上,在二进制中位置代表的就是数,就是具体的值,按照定义,小数后一位代表就是如果是1就是1 * 2的-1次方,就是0.5,在后面的十进制转换的时候要注意这点。
- 整数
- 十六进制
二进制虽然用于在计算机内部存储数据但是外部显示时,由于长度限制和与十进制转换不便,所以有了十六进制和八进制。
在十六进制中,b为16,字符集为0到9,A到F- 整数

基本上和其他进制是一样的
-
实数
整数部分和上面一样,小数部分按照位置系统的公式 如果数字是1 * 16的负一次方,转化为十进制就是0.0625。
- 整数
-
八进制
b为8,字符集为0-7-
整数
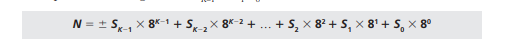
-
实数
和十六进制雷同
-
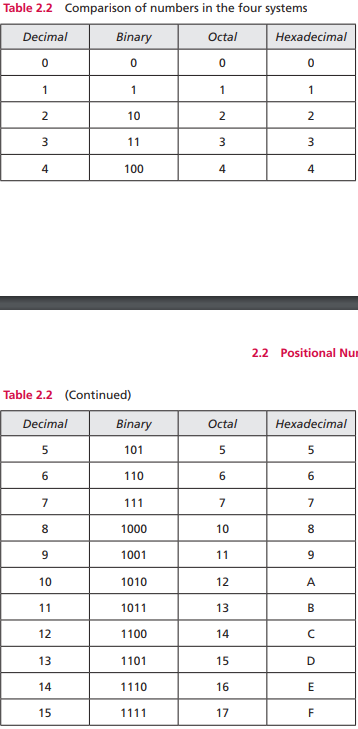
- 总结

- 十进制系统
-
各个进制之间转换
无论哪一种进制转换,这些转换都遵循位置系统的公式。
其他进制转换到十进制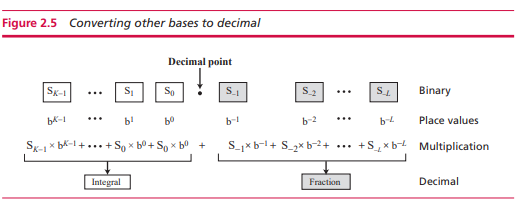
二进制转十进制 && 十六进制转十进制 && 八进制转十六进制

十进制到其他进制之间的转换
首先确定这个uml图刚刚开始很难看懂,但是实际步骤就是不断的用十进制的书处于其他进制中b,余数就是目标,就是下图中的destination,如果有商就再除,直到除尽。
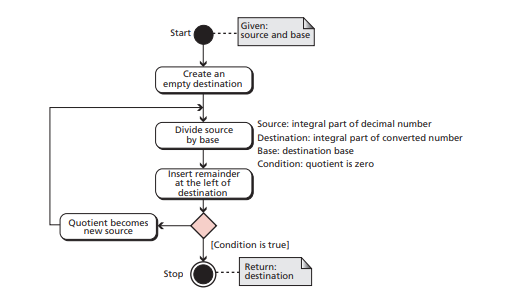
书中三个具体例子
在小数的部分上,可以使用连乘法(repetitive multiplication),将十进制小数部分不断的乘于各个进制的b,结果的整数部分为目标,如果没有整数部分,就为0,下一个接着乘b。
二进制转十六进制
前面有提到正是因为二进制显示,所以发明了十六进制和八进制,因为二进制中的四位刚好是十六进制中的一位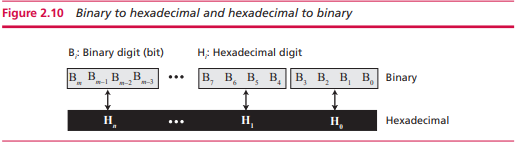
二进制转八进制
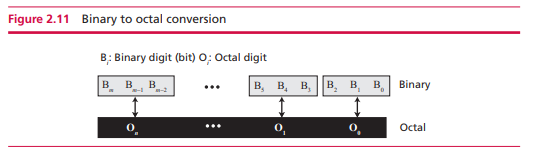
非位置化系统
罗马数字:这里直贴一下表示方法,感兴趣的可以直接买书。




