Deep Matrix Factorization Approach for Collaborative Filtering Recommender Systems
Introduction
传统的矩阵分解,诸如\(PMF ,NMF ,SVD++\),它们通过损失函数来提出优化问题,该损失函数度量协作上下文中的user和item的预期行为模型与实际行为的偏离程度。本文提出了一种新的推荐模型,该模型使用了矩阵分解范式结合深度学习,通过连续的训练来改进模型的输出。我们提出的算法是这样工作的,假设矩阵\(R\)是已知的user对item的评分,我们对\(R\)进行分解,\(R \approx P * Q\) 其中 \(P\)和\(Q\)是低秩矩阵,我们用\(E^1 = R-P*Q\)来表示矩阵分解得到的误差,关键的一点是,如果我们能够准确地预测误差,那么我们就可以通过调整模型的输出来考虑预期的误差,从而校正模型的输出。为此,我们打算深化这种矩阵分解,并且寻找误差\(E^1 \approx P^1 * Q^1\)的分解然后得到二阶误差\(E^2 = E^1-P^1 * Q^1\),为了实现对误差的更好控制,我们可以进一步细化,也就是说可以继续分解到三阶,四阶.....N阶误差。
Materials and Methods
这一章节,我们继续对上面提出的方法进行更具体的阐述。我们可以知道的是评分矩阵\(R\)是一个稀疏矩阵,因为我们对物品的评分不是一个非常普遍的行为,并且我们接触到的物品也是一个非常有限的种类。我们令物品 \(R = E^0\) ,它有个近似的稠密矩阵\(\hat{E}^0\) ,其中\(\hat{E}^0 = P^0 * Q^0 \approx E^0 = R\),后面的分解方式如上章节所阐述的类似,假设这个误差矩阵序列收敛到零,因此当我们向模型中添加新的层时,我们会得到更精确的预测,模型的结构如下:
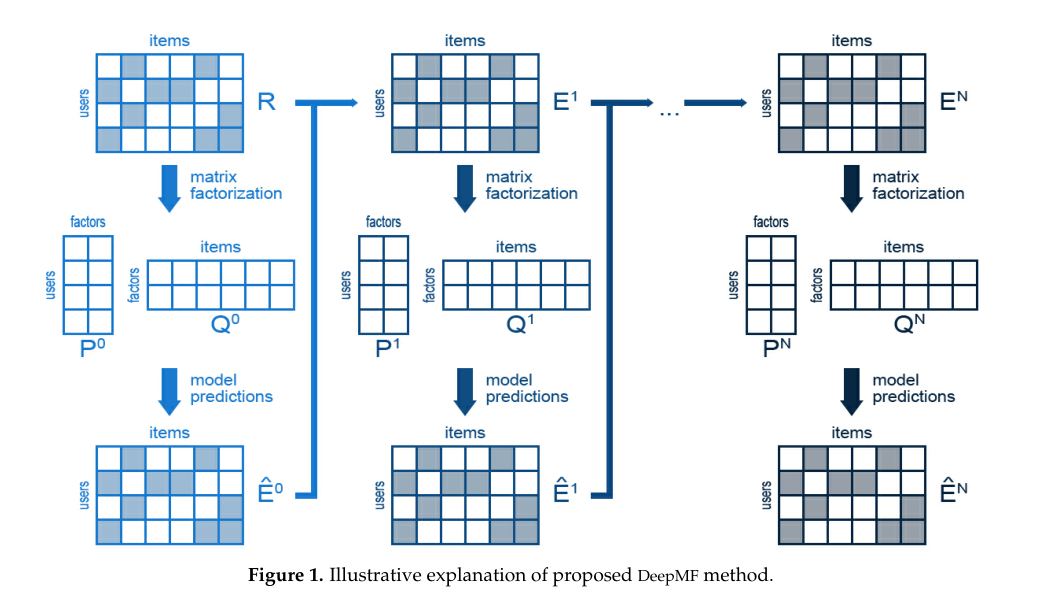
\(E^1\)中的正值表示预测过低,必须增加,而\(E^1\)中的负值表示预测过高,必须降低。如前所述,该方法的主要贡献在于其深度学习方法。这是通过对\(E^1\)误差矩阵执行新的因式分解来实现的,另外,我们分解矩阵的时候,没有要求每次分解隐层因子要一样,也就是 \(P^1 维度 n * k^1\) ,\(Q^1 维度 k^1 * m\) ,下次分解的维度不一定是\(k^1\),也可以是\(k^2\)。
第\(s\)次分解的误差我们可以推导出:
一旦深度因式分解过程在N个步骤之后结束,就可以通过将误差的估计值相加如下来重构原始评级矩阵R:
最后我们的一个损失函数:
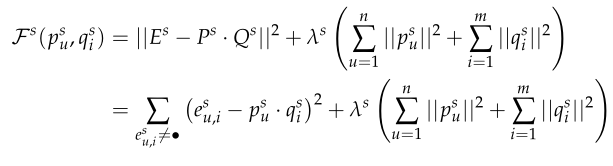
我们预测的一个结果,可以这么表示:
算法的伪代码:


Results
我们通常用MAE来评估我们方法的表现:
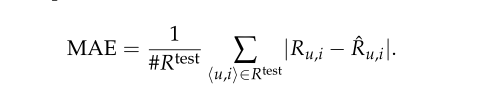
我们固定一个参数θ≥0,它扮演最小阈值的角色,以辨别用户是否感兴趣的项目。精确度定义为推荐列表的平均推荐成功率,召回率被定义为推荐列表中包含的成功推荐相对于用户喜欢的测试项目总数的平均比例:
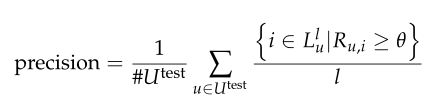
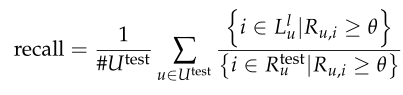
实验的数据,我们用的是下面这些数据集:

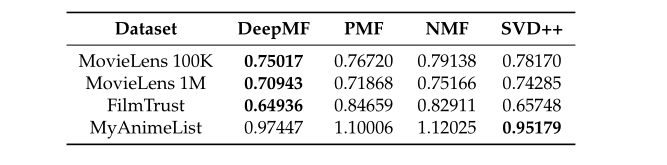
各个模型的表现情况(MAE 越低越好):
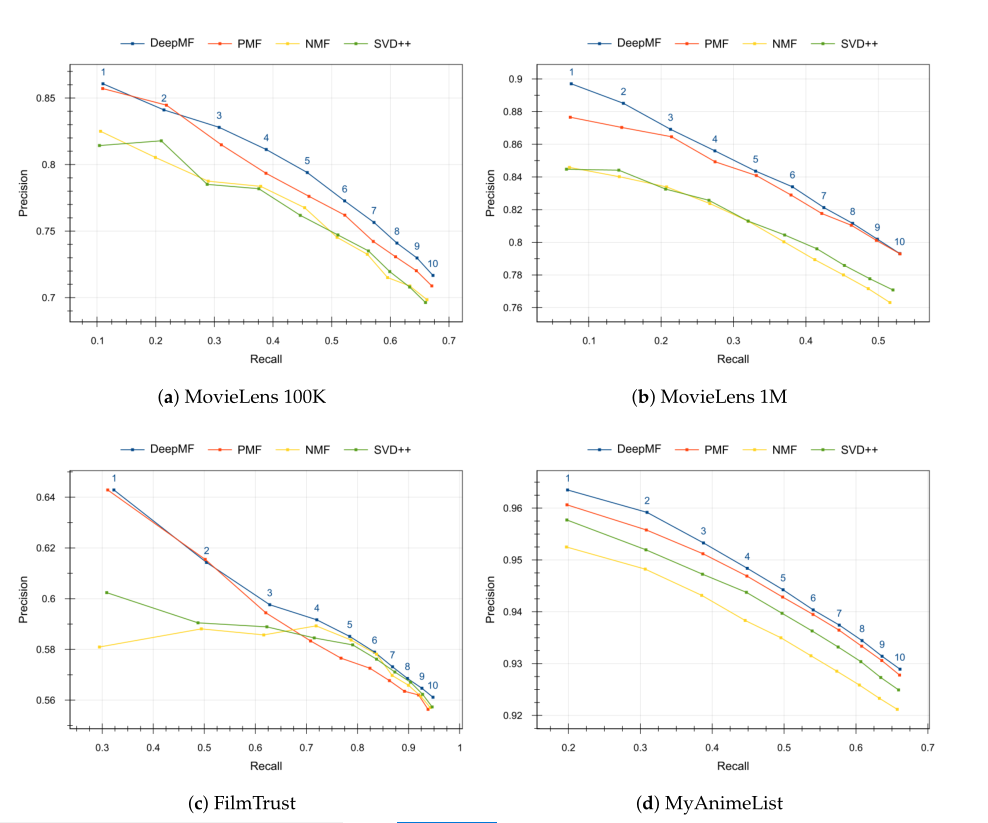
下面是top1-top10,各个模型精准率和召回率的一个表现,所谓的topK指的是,推荐排名最高的K个item,有几个是实际推荐正确的:
一项更具雄心的前瞻性工作将是将这篇论文的想法转化为一个纯粹的生物启发框架。例如,可以研究将DeepMF作为由完全连接或卷积神经网络的神经元实现的模型。这样,科学界关于网络体系结构的知识就可以用来产生更深层次、更复杂的矩阵分解嵌套模式。

 Deep Matrix Factorization Approach for Collaborative Filtering Recommender Systems 这篇文章的一个解读笔记,矩阵分解系列文章。
Deep Matrix Factorization Approach for Collaborative Filtering Recommender Systems 这篇文章的一个解读笔记,矩阵分解系列文章。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号