leetcode 84. 柱状图中最大的矩形
问题描述
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。以下是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。
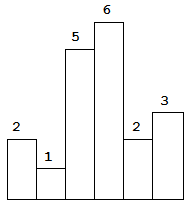
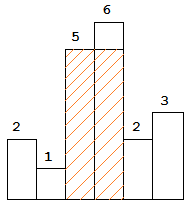
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
示例:
输入: [2,1,5,6,2,3]
输出: 10
代码1(暴力)
先给一个超出时间限制的解法,时间复杂度为\(O(N^3)\):思路很简单,我们求以left为左边矩形,right为右边矩形的面积,实际只要找中间最矮的矩形即可(这决定了矩形的宽),长为right-left+1.
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int n = heights.size();
int maxarea = 0,minheight;
for(int left = 0; left < n; left++)//left为最左边的矩形
{
maxarea = max(maxarea,heights[left]);//自己一个作为矩形
for(int right = left + 1; right < n; right++)//right为最右边的矩形
{
minheight = heights[left];
for(int k = left+1; k <= right; k++)
{
minheight = min(minheight,heights[k]);//找到最矮的矩形
}
maxarea = max(maxarea,minheight*(right-left+1));
}
}
return maxarea;
}
};
代码2(暴力优化)
我们继续分析,因为我们要求\([left,right]\)之间最矮的矩形,假如我们已经知道了\([left,right-1]\)最矮矩形高度为minheight,那只需要比较\(\min(minheight,heights[right])\)即可,因此可以省去最内层循环,时间复杂度为\(O(N^2)\),但是依然超时:
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int n = heights.size();
int maxarea = 0,minheight;
for(int left = 0; left < n; left++)//left为最左边的矩形
{
maxarea = max(maxarea,heights[left]);//自己一个作为矩形
minheight = heights[left];
for(int right = left + 1; right < n; right++)//right为最右边的矩形
{
minheight = min(minheight,heights[right]);
maxarea = max(maxarea,minheight*(right-left+1));
}
}
return maxarea;
}
};
代码3(最终暴力优化)
这个版本时间复杂度也是\(O(N^2)\),只不过加了一个类似于剪枝的操作,假如\(heights[right]\geq heights[right-1]\),则\([left,right]\)最矮的矩形一定是\([left,right-1]\)中最矮的矩形,因此可以不用考虑\([left,right-1]\)的情况了。
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int n = heights.size();
int maxarea = 0,minheight;
for(int right= 0; right < n; right++)//right为最右边的矩形
{
if(right+1 < n && heights[right+1]>=heights[right])
continue;
minheight = heights[right];
maxarea = max(maxarea,heights[right]);
for(int left = right-1; left >= 0; --left)//left为最左边的矩形
{
minheight = min(minheight,heights[left]);
maxarea = max(maxarea,minheight*(right-left+1));
}
}
return maxarea;
}
};
结果:
执行用时 :8 ms, 在所有 C++ 提交中击败了98.85%的用户
内存消耗 :15.8 MB, 在所有 C++ 提交中击败了6.95%的用户
从运行时间来看效果还不错,实际上代码1和2能够求解94/96个例子,添加的continue部分针对的就是那两个特例,一个全是1,一个是从0开始递增而已.
代码4(单调栈)
1.单调栈分为单调递增栈和单调递减栈
- 1.1 单调递增栈即栈内元素保持单调递增的栈
- 1.2 同理单调递减栈即栈内元素保持单调递减的栈
2.操作规则(下面都以单调递增栈为例)
- 2.1 如果新的元素比栈顶元素大,就入栈
- 2.2 如果新的元素较小,那就一直把栈内元素弹出来,直到栈顶比新元素小
3.加入这样一个规则之后,会有什么效果
- 3.1 栈内的元素是递增的
- 3.2 当一个栈内元素被弹出来时,说明新元素是第一个比该元素小的元素
- 3.3 因为栈内元素是递增的,所以出栈的元素前面第一个比该元素小的就是新的栈顶
其实可以把这个想象成锯木板,如果木板都是递增的那我很开心,如果突然遇到一块木板i矮了一截,那我就先找之前最戳出来的一块(其实就是第i-1块),计算一下这个木板单独的面积,然后把它锯成次高的,这是因为我之后的计算都再也用不着这块木板本身的高度了。再然后如果发觉次高的仍然比现在这个i木板高,那我继续单独计算这个次高木板的面积(应该是第i-1和i-2块),再把它俩锯短。直到发觉不需要锯就比第i块矮了,那我继续开开心心往右找更高的。当然为了避免到了最后一直都是递增的,所以可以在最后加一块高度为0的木板。
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int n = heights.size();
int maxarea = 0;
stack<int> st;
heights.push_back(0);
for(int i = 0; i < n+1; i++)
{
while(!st.empty() && heights[st.top()]>=heights[i])
{
int cur = st.top();
st.pop();
maxarea = max(maxarea,heights[cur]*(st.empty()?i:(i-st.top()-1)));
}
st.push(i);
}
return maxarea;
}
};
注意代码中i-st.top()-1实际为(i-1)-(st.top()+1)+1,其中right = i-1,left = st.top()+1.
结果:
执行用时 :16 ms, 在所有 C++ 提交中击败了64.51%的用户
内存消耗 :16.6 MB, 在所有 C++ 提交中击败了6.95%的用户




