线性代数基础知识（二）——运算和性质【转载】

 

3 运算和性质

在这一节中，我们将介绍几种矩阵/向量的运算和性质。很希望这些内容可以帮助你回顾以前知识，这些笔记仅仅是作为上述问题的一个参考。

3.1 单位矩阵与对角矩阵

单位矩阵，记作I ∈ R^n×n， 是一个方阵，其对角线上的都是1，其他元素都是0。即：

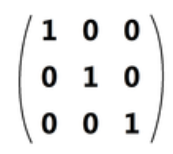
 它具备A ∈ R^m×n矩阵的所有性质

请注意，在某种意义上，标识矩阵的符号是有歧义的，因为它没有指定I的维度。一般而言，从上下文中可以推断出I的维度，这个维度使矩阵相乘成为可能。例如，在上面的等式AI = A中的I是n × n矩阵，而A = IA中 I是m × m矩阵。

对角矩阵除了对角线元素之外其他元素都是0。可以记作D = diag(d₁，d₂，...，d_n)，其中：

 

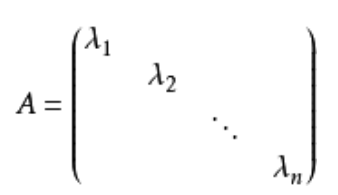
显然，I = diag(1，1，...，1).

3.2转置

矩阵的转置的是矩阵行和列的"翻转"。对于一个矩阵A ∈ R^m×n，，它的转置，A^T ∈ R^n×m，是一个n × m 的矩阵，其元素为

我们实际上已经使用转置当描述行向量的转置，因为一个列向量的转置，自然是一个行向量。

下面是一些关于转置的性质，证明起来也不太难：

• (A^T )^T = A
• (AB)^T = B^T A^T
• (A + B)^T = A^T + B^T

3.3对称矩阵

如果一个方阵A∈ R^n×n满足条件A = A^T，（行列互换后与原方阵完全相同）那么它就是对称的。如果满足A = −A^T则A是反对称的。很容易证明，任何矩阵A ∈ R^n×n，A + A^T 是对称的，而 A−A^T是反对称的。因此，任何方阵A ∈ R^n×n可以表示为一个对称矩阵和反对称矩阵的和，因为:

右边的第一个矩阵是对称的，第二个是反对称的。在实践中，对称矩阵是很常用的，他们有诸多优秀的性质，我们将在以后进行说明。我们通常将所有大小为n的对称矩阵的集合表示为Sⁿ；A ∈ Sⁿ则表示A是n × n的对称矩阵。

3.4矩阵的迹

方阵A ∈ R^n×n的迹，记作tr(A)，或可以省略括号表示成trA，是矩阵的对角线元素之和:

正如cs229讲义中所述，矩阵的迹具有以下性质（在此讲述完全是为了内容的完整性）：

• 对于A ∈ R^n×n， trA = trA^T .
• 对于A，B ∈ R^n×n， tr(A + B) = trA + trB.
• 对于A ∈ R^n×n， t ∈ R， tr(tA) = t trA.
• 对于方阵A,B,C，trABC = trBCA = trCAB，即使有更多的矩阵相乘，这个性质也不变.

前三个性质比较容易证明，咱们一起来看看第4个性质。假设A ∈ R^m×n ，B ∈ R^n×m (因此AB ∈ R^m×m是个方阵)。观察到BA ∈ R^n×n也是一个方阵，所以他的迹是有意义的。为了证明trAB = trBA，注意到：

 

在这里，第一个和最后两个等式使用了迹运算和矩阵乘法的定义。第四个等式是最重要的部分，它使用了标量乘法的交换性来交换每个乘积中因式顺序，也使用了标量加法的交换律和结合律将求和过程重新排序。

3.5范数

向量的范数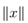是向量"长度"的非正式度量。例如，我们常用的欧氏距离（ℓ2范数）。

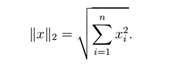向量中每个值的平方和 开根号。

注意 .

更正式的来讲，范数是满足以下4个特性的任何一个方程f : Rⁿ → R:

1. 对于任意x ∈ Rⁿ， f(x) ≥ 0 (非负性).
2. 当且仅当x = 0 时，f(x) = 0(确定性).
3. 对于任意x ∈ Rⁿ，t∈ R，f(tx) = |t|f(x) (均匀性).
4. 对于任意 x，y∈Rⁿ，f(x + y)≤f(x) + f(y) (三角不等性).

另一个范数的例子是ℓ₁范数，

以及ℓ_∞范数，

事实上，这三个范数都是ℓ_P范数家族的的例子，它包含一个实参数p≥1。ℓ_P范数定义为：

.

也可以定义矩阵A的范数，如Frobenius范数，

.

也存在许多其他的范数，但它们超出了这篇综述讨论的范围。

 

3.6线性无关和秩

对于一组向量{x₁，x₂，...x_n} ∈ R^m，如果没有向量可以表示为其余向量的线性组合，这组向量就是（线性）无关的。

相反，如果一个向量属于一个集合，这个集合中的向量可以表示为其余的向量某个线性组合，那么就称其称为向量（线性）相关。

也就是说，对于一些标量值α₁，...，α_n−1 ∈ R，如果

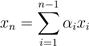
我们说向量x₁，...，x_n是线性相关；否则，该向量线性无关。例如，向量

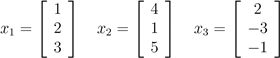
x1，x2 和 x3 是线性相关的，因为x₃ = −2x₁ + x₂.

矩阵A ∈ R^m×n的列秩是所有线性独立的列的最大子集的大小。

列秩通常指矩阵A线性无关的列的数目。相似的，将A的行构成一个线性无关集，行秩是它行数的最大值。

对任意矩阵A ∈ R^m×n，其列秩与行秩是相等的（虽然我们不打算证明），所以我们将两个相等的秩统称为A的的秩。秩的一些基本性质如下：

• 对于 A ∈ R^m×n， rank(A) ≤ min(m，n). 如果rank(A) = min(m，n)， 则称A满秩。
• 对于 A ∈ R^m×n， rank(A) = rank(A^T ).
• 对于 A ∈ R^m×n， B ∈ R^n×p， rank(AB) ≤ min(rank(A)，rank(B)).
• 对于 A，B ∈ R^m×n， rank(A + B) ≤ rank(A) + rank(B).

3.7逆

矩阵A ∈ R^n×n的逆，写作A⁻¹，是一个矩阵，并且是唯一的。

A⁻¹A = I （单位矩阵）= AA⁻¹

注意不是所有的矩阵都有逆。例如非方阵，是没有逆的。然而，即便对于一些方阵，它仍有可能不存在逆（只有部分方阵是可逆的）。

如果A⁻¹存在，我们称矩阵A 是可逆的或非奇异的；

如果A⁻¹不存在，则称矩阵A不可逆或奇异；

如果一个方阵A有逆A⁻¹，它必须满秩。我们很快可以看到，除了满秩，矩阵可逆还有许多充分必要条件。

满足以下的性质的矩阵可逆；以下所有叙述都假设A，B ∈ R^n×n是非奇异的：

• (A⁻¹)⁻¹ = A
• (AB)⁻¹ = B⁻¹A⁻¹
• (A⁻¹)^T = (A^T )⁻¹. 因此这样的矩阵经常写作A^−T

举一个矩阵的逆的应用实例。对于线性方程组Ax = b，其中 A ∈ R^n×n，并且x，b ∈ Rⁿ.如果A是非奇异（即可逆），则x = A⁻¹b（如果A ∈ R^m×n不是方阵呢？是否成立？）

3.8 正交矩阵

如果x^T y = 0，则两个向量 x，y ∈ Rⁿ是正交的。对于一个向量x ∈ Rⁿ，如果则是x归一化的（向量的2范数为1）。对于一个方阵U ∈ R^n×n，如果所有列都是彼此正交和归一化的，（列就称为标准正交）则这个方阵是正交的（注意在讨论向量或矩阵时，正交具有不同的含义）。

根据正交和归一化的定义可得：

U^T U = I = UU^T

换言之，一个正交矩阵的逆矩阵的是它的转置。我们一般只使用正交这个术语来描述U为方阵的情形。

非方阵正交：注意，如果U不是方阵的，也就是说， U ∈ R^m×n，n < m，但它的列仍然是正交的，则U^T U = I，但UU^T ≠ I.等。【左* 与 右* 有区别】

另一个正交矩阵的很好的属性是，向量与正交矩阵的运算将不会改变其欧氏范数，即对于任意x ∈ Rⁿ，正交的U ∈ R^n×n：

3.9矩阵的值域和零空间

一组向量{x₁，x₂，...x_n}的值域是{x₁，x₂，...x_n}线性组合的所有向量的集合。即

可以看出如{x₁，...，x_n}是一组n个线性无关的向量，其中x_i ∈ Rⁿ，则({x₁，...x_n}) 的值域= Rⁿ。换句话说，任何向量v ∈ Rⁿ可以写成x₁ 至 x_n的线性组合。向量y ∈ R^m 在值域 {x₁，...，x_n}上的投影 (假定 x_i ∈ R^m) 是向量v ∈ span({x₁，...x_n})，则通过比较其欧式范数，v 与 y无限接近。这个投影记作Proj（Y；{ x1，…，n}）,可以定义它为，

A ∈ R^m×n的值域（有时也被称为列空间），表示为R(A)，就是A的值域。换言之，

R(A) = {v ∈ R^m : v = Ax，x ∈ Rⁿ}.

我们假设A满秩且n < m，向量y ∈ R^m 在A值域上面的投影可以表示为

这最后一个方程应该看起来非常熟悉，因为它几乎是我们在课上用于参数的最小二乘估计公式（并且我们可以快速再次推导出来）几乎相同的。看一下投影的定义，你会发现这其实与我们在解决最小二乘法问题时进行最小化的目的是相同的（除了范数是一个平方，这并不影响求得最优的点），所以这些问题是有自然联系的。当 A 仅含有1个单独的列 a ∈ R^m，则出现了向量在一条直线上投影的特殊情况。

矩阵A ∈ R^m×n的零空间，记为N(A)，是被A乘后，得到的所有等于0的向量一个集合，即，

N(A) = {x ∈ Rⁿ : Ax = 0}.

注意，向量R(A)的大小为m，而N(A)的大小为n，所以 R(A^T ) 和 N(A) 的向量都在 Rⁿ中。事实上，我们可以讨论更多。

换句话说，R(A^T ) 和 N(A)是不相交的子集，一同跨越了Rⁿ整个空间。这种类型的集合称为正交互补，写作R(A^T ) = N(A)^⊥.