MZOJ 1133 && LuoGu P1352 没有上司的舞会 の 题解
MZOJ 1133 && LuoGu P1352 没有上司的舞会 [传送门]
题目描述
某大学有N个职员，编号为1~N。他们之间有从属关系，也就是说他们的关系就像一棵以校长为根的树，父结点就是子结点的直接上司。现在有个周年庆宴会，
宴会每邀请来一个职员都会增加一定的快乐指数Ri，但是呢，如果某个职员的上司来参加舞会了，那么这个职员就无论如何也不肯来参加舞会了。
所以，请你编程计算，邀请哪些职员可以使快乐指数最大，求最大的快乐指数。
输入输出格式
输入格式：
第一行一个整数N。(1<=N<=6000)
接下来N行，第i+1行表示i号职员的快乐指数Ri。(-128<=Ri<=127)
接下来N-1行，每行输入一对整数L,K。表示K是L的直接上司。
最后一行输入0 0
输出格式：
输出最大的快乐指数。
输入输出样例
7 1 1 1 1 1 1 1 1 3 2 3 6 4 7 4 4 5 3 5 0 0
输出样例：
5
这道题...怎么说呢...
似曾相识...嗯对似曾相识（何止是似曾相识...简直跟战略游戏一模一样嘛，只是它把f[u][0]和f[u][1]换了下位置罢了...）
大概就是老样子
用f[u][0]表示在节点u不放置人，用f[u][1]表示在节点u要放置人；
我们知道当节点u要放置人时，它的子节点v必须不放置人才能让快乐指数（背对疾风吧！hasaki）达到max；
同理，节点u不放置人的时候，它的子节点v可以选择放置人或者不放置人都可以，所以我们取其中的最大值；
（图在这里↓）
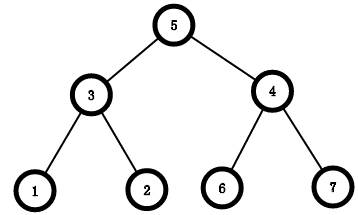
那么，状态转移方程就出来了：f[u][0]+=max(f[v][0],f[v][1])；（此时u不放置人）
或 f[u][1]+=f[u][0]；
状态转移方程出来了就简单了吖
但实际上还有一个问题，大家应该都发现了这个根节点的不定的问题，也就是说这棵树的根是不确定的，该怎么办呢？
答案巨型九头简单
那就是
不！管！它！
这是为什么呢？？？
其实我们不妨设置1就为根节点，建边的时候双向建边就行了，最后在dp模块里判定一下让u==v的时候为无效状态就ok。
（图就变成了这样子↓）
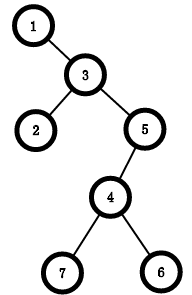
所以一眼就看出来了
都是隔一个节点放置一个人嘛
所以没什么影响啊
那么，代码如下：
#include<bits/stdc++.h>
#define maxn 100000
#define maxm 10000
using namespace std;
int N;
int head[maxm],k=0;
int R[maxm];
int f[maxn][2];
struct node{
int u,v,nxt;
}e[maxn];
void adde(int u,int v){
e[k].v=v;
e[k].nxt=head[u];
head[u]=k++;
}
void init(){
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
}
void readdata(){
memset(head,-1,sizeof(head));
int u,v;
scanf("%d",&N);
for(int i=1;i<=N;i++){
scanf("%d",&R[i]);
}
for(int i=1;i<N;i++){
scanf("%d%d",&u,&v);
adde(u,v);
adde(v,u);
}
}
void dp(int u,int fa){
f[u][0]=0;f[u][1]=R[u];
for(int i=head[u];~i;i=e[i].nxt){
int v=e[i].v;
if (v==fa) continue;
dp(v,u);
f[u][1]+=f[v][0];
f[u][0]+=max(f[v][0],f[v][1]);
}
}
void work(){
dp(1,0);
printf("%d",max(f[1][0],f[1][1]));
}
int main(){
//init();
readdata();
work();
return 0;
}
总的来说还是比较简单（反正比选课简单到哪去了（手动不爽））
