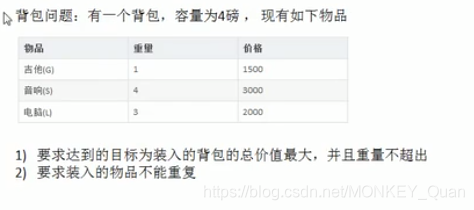
背包问题
背包问题解决:



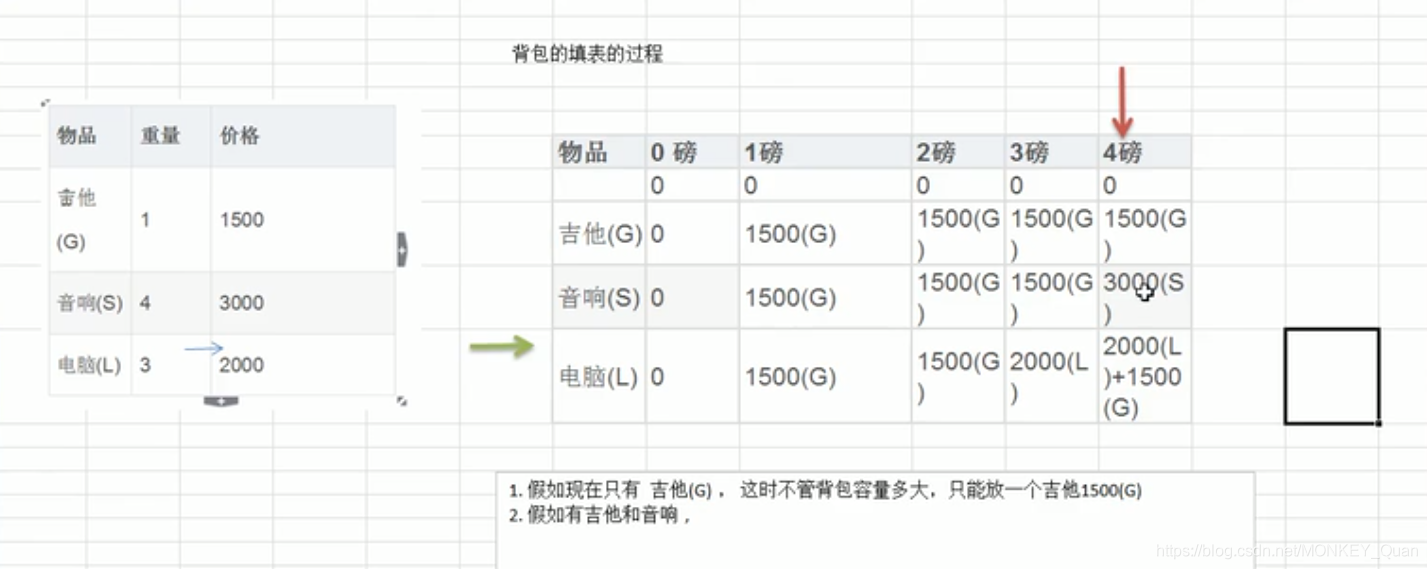

代码:
public class KnapsackProblem {
public static void main(String[] args) {
int []w={1,4,3};//物品的重量
int []val={1500,3000,2000};//物品的价值 这里的val[i],就是前面的v[i]
int m=4;
int n=val.length;
//创建一个二维数组
// v[i][j] 表示在前i个物品中能够装入容量为j的背包中的最大价值
int [][]v=new int[n+1][m+1];
//为了记录放入商品的情况,我们定一个二维数组
int[][] path=new int[n+1][m+1];
//初始化第一行第一列 默认数组第一行第一列为0
for(int i=0;i<v.length;i++){
v[i][0]=0;//设置第一列为0
}
for(int i=0;i<v[0].length;i++){
v[0][i]=0;//设置第一行为0
}
//根据前面得到的公式啦动态规划处理
for(int i=1;i<v.length;i++){//不处理第一行 i是从一开始的
for(int j=1;j<v[0].length;j++){//处理第一列,j从1开时
if(w[i-1]>j){ //因为我们程序i是从1开始的,因此原来公式中的w[i] 修改成w[i-1]
v[i][j]=v[i-1][j];
}else{
//说明
//因为我们的i 从1开始,因此公式需要调整成
//v[i][j]=Math.max(v[i-1][j],val[i-1]+v[i-1][j-w[i-1]]);
if(v[i-1][j]<val[i-1]+v[i-1][j-w[i-1]]){
v[i][j]=val[i-1]+v[i-1][j-w[i-1]];
//把当前的情况记录到path
path[i][j]=1;
}else{
v[i][j]=v[i-1][j];
}
}
}
}
for(int i=0;i<v.length;i++){
for(int j=0;j<v[i].length;j++){
System.out.print(v[i][j]+" ");
}
System.out.println();
}
//输出最后我们是放入的哪些商品
//这样会把所有的放入情况得到,其实我们只需要最后的放入
/*for(int i=0;i<path.length;i++){
for(int j=0;j<path[i].length;j++){
if(path[i][j]==1){
System.out.printf("第%d个商品放入到背包\n",i);
}
}
}
*/
//
int i=path.length-1;//行的最大下标
int j=path[0].length-1;//列的最大下标
while(i>0){//从path的最后开始找,切记需要减去刚放入的商品的重量
if(path[i][j]==1){
System.out.printf("第%d个商品放入到背包\n",i);
j-=w[i-1];//w[i-1]
}
i--;
}
}
}

