Python之递归函数

在函数内部，可以调用其他函数。如果一个函数在内部调用自身本身，这个函数就是递归函数。

举个例子，我们来计算阶乘 n! = 1 * 2 * 3 * ... * n，用函数 fact(n)表示，可以看出：

fact(n) = n! = 1 * 2 * 3 * ... * (n-1) * n = (n-1)! * n = fact(n-1) * n

所以，fact(n)可以表示为 n * fact(n-1)，只有n=1时需要特殊处理。

于是，fact(n)用递归的方式写出来就是：

def fact(n):
    if n==1:
        return 1
    return n * fact(n - 1)

上面就是一个递归函数。可以试试：

>>> fact(1)
1
>>> fact(5)
120
>>> fact(100)
9332621544394415268169923885626670049071596826438162146859296389521759999322991560894146397615651

8286253697920827223758251185210916864000000000000000000000000L

如果我们计算fact(5)，可以根据函数定义看到计算过程如下：

===> fact(5)
===> 5 * fact(4)
===> 5 * (4 * fact(3))
===> 5 * (4 * (3 * fact(2)))
===> 5 * (4 * (3 * (2 * fact(1))))
===> 5 * (4 * (3 * (2 * 1)))
===> 5 * (4 * (3 * 2))
===> 5 * (4 * 6)
===> 5 * 24
===> 120

递归函数的优点是定义简单，逻辑清晰。理论上，所有的递归函数都可以写成循环的方式，但循环的逻辑不如递归清晰。

使用递归函数需要注意防止栈溢出。在计算机中，函数调用是通过栈（stack）这种数据结构实现的，每当进入一个函数调用，栈就会加一层栈帧，每当函数返回，栈就会减一层栈帧。由于栈的大小不是无限的，所以，递归调用的次数过多，会导致栈溢出。可以试试计算 fact(10000)。

任务

汉诺塔 (http://baike.baidu.com/view/191666.htm) 的移动也可以看做是递归函数。

我们对柱子编号为a, b, c，将所有圆盘从a移到c可以描述为：

如果a只有一个圆盘，可以直接移动到c；

如果a有N个圆盘，可以看成a有1个圆盘（底盘） + (N-1)个圆盘，首先需要把 (N-1) 个圆盘移动到 b，然后，将 a的最后一个圆盘移动到c，再将b的(N-1)个圆盘移动到c。

请编写一个函数，给定输入 n, a, b, c，打印出移动的步骤：

move(n, a, b, c)

例如，输入 move(2, 'A', 'B', 'C')，打印出：

A --> B

A --> C

B --> C

 

 

函数 move(n, a, b, c) 的定义是将 n 个圆盘从 a 借助 b 移动到 c。

参考代码:

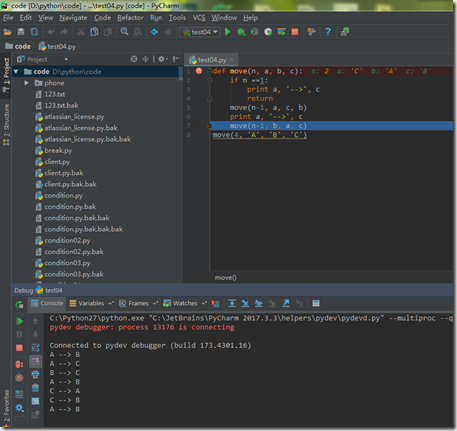
def move(n, a, b, c):
    if n ==1:
        print a, '-->', c
        return
    move(n-1, a, c, b)
    print a, '-->', c
    move(n-1, b, a, c)
move(4, 'A', 'B', 'C')

 

A --> B
A --> C
B --> C
A --> B
C --> A
C --> B
A --> B
A --> C
B --> C
B --> A
C --> A
B --> C
A --> B
A --> C
B --> C

Debug 了解一下递归算法吧