C语言复合梯形公式实现定积分
假设被积函数为
f
x
，积分区间为
,
a
b
，把区间
,
a
b
等分成
n
个小区间，
各个区间的长度为
h
，即
/
h
b
a
n
，称之为“步长”
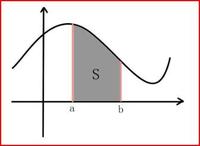
。根据定积分的定义及几
何意义，定积分就是求函数
f
x
在区间
,
a
b
中图线下包围的面积。将积分
区间
n
等分，各子区间的面积近似等于梯形的面积，面积的计算运用梯形公
式求解，再累加各区间的面积，所得的和近似等于被积函数的积分值，
n
越
大，所得结果越精确。以上就是利用复合梯形公式实现定积分的计算的算法思
想。
复合梯形公式：
假设被积函数为f(x)，积分区间为[a,b] ，把区间[a,b]等分成n个小区间，各个区间的长度为step，即step=(b-a)/n，称之为“步长”。根据定积分的定义及几何意义，定积分就是求函数f(x)在区间[a,b]中图线下包围的面积。将积分区间n等分，各子区间的面积近似等于梯形的面积，面积的计算运用梯形公式求解，再累加各区间的面积，所得的和近似等于被积函数的积分值n越大，所得结果越精确。以上就是利用复合梯形公式实现定积分的计算的算法思想。
复合梯形公式：
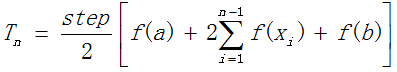
具体源代码如下：
1 #include <math.h>
2 #include <stdio.h>
3
4 double integral(double(*fun)(double x), double a, double b, int n)
5 {
6 double sum,step,result;
7 int i;
8 sum=(fun(a)+fun(b))/2;
9 step=(b-a)/n; /*积分步长*/
10 for(i=1;i<n;i++)
11 sum=sum+fun(a+i*step);
12 result=sum*step;
13 return result;/*返回积分值*/
14 }
15
16 double function(double x)
17 {
18 return (x*sin(x)); /*修改此处可以改变被积函数*/
19 }
20
21 void main()
22 {
23 double result;
24 result=integral(function,1.0,2.0,150);/*修改此处可以改变积分上下限和步长*/
25 printf("result=%f\n",result);
26 }
注：double(*fun)(double x)，定义函数指针
参考：用C语言求积分
